Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Скорости и ускорения точек вращающегося телаСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Если тело вращается вокруг оси, то его точки перемещаются по окружностям (рис. а), радиусы которых г равны расстояниям точек от оси вращения. Рассмотрим точку М, которая за время dt прошла путь ds = ММ1. В данном случае путь ds можно определить как произведение угла поворота на радиус окружности, т. е. ds = r * dφ. 10 Линейная скорость определится как производная пути по времени
v = ds/dt Подставив вместо ds его значение по (10), получим
Подставив в формулу для линейной скорости точек тела, вращающегося вокруг неподвижной оси, значение частоты вращения в оборотах в минуту (об/мин), получим
v = Касательное ускорение точки вращающегося тела определяется из выражения
at = dv/dt = d(rω)/dt = r * dω/dt = rε Нормальное ускорение точки равно отношению квадрата скорости к радиусу окружности an = v2/r Пример7. Скорость точки за 15 с. возрастает от 20 км/ч до 80 км/ч. Определить какой путь пройдет точка за время разгона и каково будет ее ускорение в конце 15 – ой секунды если движение происходит по дуге r = 50 м.
Дано: v0 t = 15 c v0 = 20 км/ч = 5,6 м/с v1 = 80 км/ч = 22,3 м/с R r= 50 м Определить S; at; an v1 at = v – v0 /t = 22,3 – 5,6 /15 = 1,12 м/с ап = v 2/r = 22,32 / 50 = 10 м/с2 a = S = (v0 + v) * t /2 = (5,6+22,3) * 15 / 2= 210м
Пример 8. Автомобиль движется со скоростью v = 54 км/ч при торможении он получает замедление at = - 0,5 м/с2. Найти какой путь он прошел от начала торможения до полной остановке и сколько времени продолжалось торможение. Дано: v0 = 54км/ч = 15 м/с v0 v1 at = -0,5 м/с2
Определить S;t at = v – v0 /t => t = v – v0 / at = 0-15 / -0,5 = 30 c S = (v0 + v) * t /2 = (15+0)*30 / 2 = 225м Пример 9. На пути 600 м скорость точки уменьшается с 30 до 10 м/с. Определить время этого движения, а также полное ускорение в начале и в конце движения если точка двигалась по дуге r = 400м. Дано: S = 600 м v0 v0 = 30 м/с v1 = 10 м/с r = 400 м r Определить t;a1;a2 v1 S = (v0 + v) * t /2 => t = 2S / v0 + v1 = 2 * 600 / 30+10 = 30c at1 = v – v0 /t = 10-30 / 30 = - 0,67 м/с2 ап1 = v 02/r = 302/400 = 2,25 м/с2 a1 = аt1= аt2= - 0,67 м/с2 ап2 = v 12/r = 102/400=0,25м/с2 a2 =
Пример 10. Точка начала прямолинейное равноускоренное движение из состояния покоя и ч/з 5сек приобрела скорость 10 м/с с этого момента точка стала двигаться равномерно по окружности r = 10 м, ч/з 15 сек движение по окружности точка внезапно остановилась. Определить: 1. Путь пройденный точкой за все время движения; 2. Среднюю скорость на этом пути; 3. Ускорение точки на прямолинейном и криволинейном участке пути. Дано: 0 at v1 1 v0 = 0 t1 = 5 с v1 = v2 v1 = 10 м/с r r = 10 м an t2 = 15 с Определить S; v; at1; an2 S1 = vср * t1 = v1* t1 / 2 = 10 * 5 / 2 = 25м (т. к. равномерноускоренное) S2 = v2 * t2 = 10 * 15 / 2 = 150м(т.к. равномерное) S = S1 + S2 = 25 + 150 = 175 м vср = S / t1 + t2 = 175 / 20 = 8,75 м/с = 8,75 * 3,6 = 31,5 км /ч at1 = v1 / t1 = 10 / 2 = 2 м/с an = v2 / r = 102 / 10 = 100 / 10 = 10 м/с Пример 11. Автомобиль, имея начальную скорость 72 км/ч проходит за 20 сек путь 600. Найти скорость и ускорение (полное) в конце 20 сек, считая движение равнопеременным по дуге окружности радиуса r = 1200 м Дано: v0 = 72 км/ч= 20 м/с t = 20 с S = 600 м r r = 1200 м Определить v; a S = v0 + v /2 * t => v = 2S / t – v0 = 2 * 600 / 20 – 20 = 40 м/с at = v – v0 /t = 40 – 20 / 20 = 1 м/с2 ап = v 2/r = 402 / 1200 = 1,3 м/с2 а = √аt2 + an2 = √12 + 1,32 = 1,6 м/с2 Пример 12. Точка прошла за время 20 сек с касательным ускорением at = 4 м/с2 путь 1400 м по дуге r = 100 м. Определить v0, а
Дано: at = 4 м/с2 t = 20 с S = 1400 м r r = 100 м Определить v0; a S = v0 * t + at * t2 / 2 => v0 = S - at * t2 / 2 /t = 1400 – 4* 202/20 = 30м/с at = v – v0 /t => v = at * t + v0 = 4 * 20 + 30 = 110 м/с2 ап = v 2/r = 1102 / 100 = 121 м/с2 а = √аt2 + an2 = √1212 + 42 = 121,1м/с2
Пример 1. Равномерно вращающееся тело делает 10800 оборотов в час. Определить его угловую скорость. Дано: n = 10800 об/час = 10/800: 60 = 180 об/мин ω = π * n / 30 = 6 π рад / сек ___________ ω -? Пример 2. Угловая скорость равномерно вращающегося тела ω = 8 рад / сек. Определить сколько оборотов в час делает тело. Дано: ω = 8 рад / сек __________ ω = π * n / 30 => n = 30 * ω / π=76,4 об/мин = 60 * 76,4 = 4585 об/ч n -?об/ч
Пример 3. Расстояние от Луны до Земли рано 384000 км. Найти скорость движения Луны по своей орбите, если полный оборот около Земли она совершает в 27 суток. Орбиту Луны принять за окружность, а движение считать равномерным. Дано: 27 суток = 27 * 24 * 3600 = 2332800 сек r = 384000 км Sкруга = π D = 2π r = 2 * 3,14 * 384000000м = 2411520000 м t = 27 суток v = s / t = 2411520000 / 2332800 = 1034 м / c _________ v -?
Пример 4. Дано: r = 149600000 км – расстояние от земли до солнца t = 365 дней = 365 * 24 * 3600 = 31536000 сек _________ v -? – земли вокруг солнца Sкруга = π D = 2π r = 2 * 3,14 * 149600000000м v = s / t = 29791 м / сек Пример 5. Вал, начинает вращаться равноускоренно из состояния покоя, в первые 10 сек совершает 30 оборотов. Какова его угловая скорость по истечению 5 сек? Дано: t1 = 10 сек φоб = φ / 2π => φ = φоб * 2π = 188,4 рад φ = 30 об t2 = 5 сек φ = ω * t / 2 => ω = 2φ / t = 2 * 188,4 / 10 = 37,68 рад/сек(при10 сек) ω0 = 0 ___________ ω -? ω = 37,68 / 2 = 18,84 рад / сек (при 5 сек)
Пример 6. Вал, начинает вращаться равноускоренно из состояния покоя, делает 4800 об в первые 2 мин. Найти угловое ускорение вала.
Дано: φ = 4800 об φоб = φ / 2π => φ = φоб * 2π = 4800 * 2 * 3,14 = 30144 рад. ω0 = 0 t = 2 мин φ = ε * t2 / 2 => ε = 2φ / t2 = 2 * 30144 / 1202 = 4,18 рад / сек2 __________ ε -? Пример 7. Колесо начинает вращаться равноускоренно из состояния покоя, Через 20 мин после начала движения колесо имело угловую скорость, соответствующую 240 об / мин. Сколько оборотов сделало колесо за эти 20 мин. Дано: ω0 = 0 t = 20 мин φ = ω * t / 2 = 240 * 20 / 2 = 2400 об ω = 240 об / мин _________ φ -?
Пример 8. Колесо, вращающееся вокруг неподвижной оси с угловой скоростью ω = 4π рад/сек, было затем отключено от привода, поддерживавшего заданную рабочую скорость вращения. Сделав 25 оборотов, колесо вследствие трения в подшипниках остановилось. Полагая вращение равнозамедленным, определить угловое ускорение колеса. Дано: ω0 = 4π рад/с ε = ω – ω0 / t = 0 - 4π / t = - 4π / t φ = 25 об φ = φоб * 2π = 25 * 2 * 3,14 = 157 рад ω = 0 φ = ω + ω0 / 2 * t = ω0 * t / 2 => t = 2φ / ω0 = 2 * 157 /4π = 25 сек _________ ε -? ε = -4π / t = 4 * 3,14 / 25 = - 0,5 рад / сек2 Пример 9. При посадке самолета пропеллер вращается с угловой скоростью, соответствующей п = 900 об/мин. После выключения мотора пропеллер сделал до остановки 60 оборотов. Считая вращение пропеллера после выключения мотора равнозамедленным, определить, сколько времени прошло с момента выключения мотора до остановки. Определить ускорение пропеллера. Дано: n = 900 об/мин φоб = φ / 2π => φ = φоб * 2π = 60 * 2 * 3,14 = 376,8 рад φ = 60 об ω0 = π n / 30 = 3,14 * 900 / 30 = 94,2 рад / сек ω = 0 φ = ω + ω0 / 2 * t = 0 + ω0 * t / 2 => t = 2φ / ω0 = 2 * 376,8 / 94,2 = 8 сек _________ t -? ε -? ε = ω – ω0 / t = 0 – ω0 / t = 94,2 / 8 = 11,775 рад / сек2 Пример 10. Маховое колесо радиуса R = 2 м вращается равноускоренно из состояния покоя; через t =10 сек точки, лежащие на ободе, обладают линейной скоростью v = 50 м/сек. Найти скорость, нормальное и касательное ускорения точек обода колеса для момента t = 25 сек. Дано: r = 2 м v1 = r * ω => ω = v / r = 50 / 2 = 25 рад/сек ω0 = 0 ε = ω1 / t1 = 25 / 10 = 2,5 рад/сек2 t1 = 10 с ε = ω2 / t2 => ω2 = ε * t = 2,5 * 25 = 62,5 рад / сек v1 = 50 м/с v2 = r * ω2 = 2 * 62,5 = 125 м/с t2 = 25 с at = r * ε = 2 * 2,5 = 5 м/с2 v2 -? an -? at -? an = v22 / r = 1252 / 2 = 7812,5 м/с2
Пример 11. Точка пробегает в минуту 200 раз окружность, диаметр которой 3 м. Вычислить ускорение точки. Дано: ω = π n / 30 = 3,14 * 200 / 30 = 20,9 рад/сек n = 200 об/мин v = r * ω = 1,5 * 20,9 = 31,4 м/с D = 3м an = v22 / r = 31,42 / 1,5 = 660 м/с ________ an -? Пример 12. Частота вращения маховика составляет 300 об/мин затем маховик бал заторможен и ч/з 3 с частота его вращения уменьшилась до 120 об/мин. Определить ч/з сколько времени маховик остановится и сколько оборотов он совершит от начала торможения до полной остановки. Дано: n0 = 300об/мин ω0 = πn0 / 30 = 300π / 30 = 10π рад/сек t1 = 3c ε = const ω1 = πn1/ 30 = 120π / 30 = 4π рад/сек n1 = 120об/мин ε = ω1 - ω0 / t1 = 4π - 10π / 3 = - 2π рад/сек2 n2 = 0 ω2 = ω0 + ε t2 т к ω0 = 0 то => ω2 = 0 - ω0 = ε t2 => t2 = - ω0 / ε = -10π / - 2π = 5с _________ φ = ωср * t = (ω0 + ω2) * t /2 = 10π * 5 / 2 = 25π рад t2 -? φ -? φоб = φ / 2π = 25π / 2π = 12,5 об Пример 13. Ротор эл двигателя делает 2700 об/мин. После выключения ротор останавливается совершив 675 об. Определить время вращения ротора с момента выключения до полной остановки. Дано: n0 = 2700об/мин ω0 = πn0 / 30 = 2700π / 30 = 90π рад/сек t1 = 3c φоб = φ / 2π => φ = 2π φ0 = 2π675 = 1350 рад n1 = 0 φ = ωср * t = (ω0 + ω1) * t /2 ω1 = 0 t = 2φ / ω0 + ω1 = 2 * 1350 / 90π = 30с φ = 675 об _________ t -?
Пример 14. Тело при вращении с постоянным угловым ускорением 24 рад/с2 в течении 105 сек сделано 2100 об. Определить угловую скорость тела в начале и конце равнозамедленного вращения. Дано: t = 105 сек φ = 2π φ0 =2π * 2100 = 4200π рад φоб = 2100 об φ = ω0 * t + ε* t2 / 2 => ω0 = φ - ε* t2 / 2 / t = ε = 24 рад/с2 4200 – 24 * 1052 / 2/105 = 1220 рад/сек -------------- ω0 -? ω -? ω = ω0 + ε * t = 1220 + 24 * 105 = 3740 рад/сек
Подставив в выражение нормального ускорения ап = v 2 / r значение скорости v = ωr, получим an = v2/r = (ωr)2/r = rω2
Значение полного ускорения вычисляется как диагональ прямоугольника, построенного на составляющих ускорениях at и ап (рис. б). Подставив значения касательного и нормального ускорений, получим
Направление вектора полного ускорения точки вращающегося тела можно определить по углу а, образованному этим вектором с радиусом
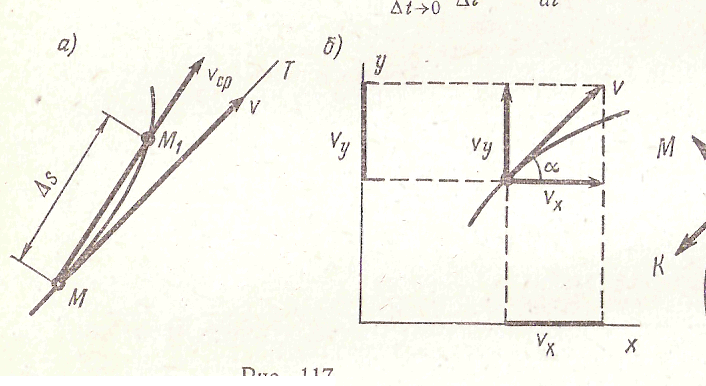
Если точка за равные промежутки времени проходит неравные пути, то ee движение называется неравномерным. Скорость неравномерного движения есть величина переменная и является функцией времени v = f (t). 5 Рассмотрим точку М, которая перемещается по заданной траектории по некоторому закону s = f (t). За промежуток времени Δt точка М переместится в положение М1 по дуге ММ1. Если промежуток времени Δt мал, то дугу можно заменить ее хордой и найти в первом приближении среднюю скорость движения точки v ср = Δs/Δt Средняя скорость направлена по хорде от точки М к точке М1. Если постепенно уменьшать промежуток времени Δt, то уменьшается и пройденный путь Δs, т. е. в пределе при Δt → 0 значение средней скорости приближается к значению скорости в заданный момент t т. е. истинную скорость найдем путем перехода к пределу при Δt →0 v = lim Δs/Δt = ds/dt 6 ∆t→0 При Δt → О направление хорды в пределе совпадает с направлением касательной к траектории в точке М, т. е. значение скорости точки определяется как производная пути по времени, а направление ее совпадает с касательной к траектории в данной точке.
Если точка за равные промежутки времени проходит неравные пути, то ee движение называется неравномерным. Скорость неравномерного движения есть величина переменная и является функцией времени v = f (t). 5 Часто бывает необходимо определить среднюю скорость неравномерного движения за некоторый промежуток времени, т. е. скорость такого воображаемого равномерного движения, при котором точка проходит за определенный промежуток времени такой же путь, как и при неравномерном движении. Пусть S — путь, проходимый точкой при неравномерном движении, и t — время, за которое точка проходит этот путь. Средняя скорость определится по формуле v ср = s / t Рассмотрим точку М, за промежуток времени Δt точка М переместится в положение М1 по дуге ММ1. Если промежуток времени Δt мал, то дугу можно заменить ее хордой и найти в первом приближении среднюю скорость движения точки v ср = Δs/Δt Средняя скорость направлена по хорде от точки М к точке М1. Если постепенно уменьшать промежуток времени Δt, то уменьшается и пройденный путь Δs (хорда стремится к дуге), т. е. в пределе при Δt → 0 значение средней скорости приближается к значению истиной скорости в момент t т. е. истинную скорость найдем путем перехода к пределу при Δt →0 v = lim Δs/Δt = ds/dt 6 ∆t→0 При Δt → О направление хорды в пределе совпадает с направлением касательной к траектории в точке М, т. е. значение скорости точки определяется как производная пути по времени, а направление ее совпадает с касательной к траектории в данной точке.
|
||||
|
Последнее изменение этой страницы: 2016-04-25; просмотров: 2286; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.147.27.154 (0.009 с.) |

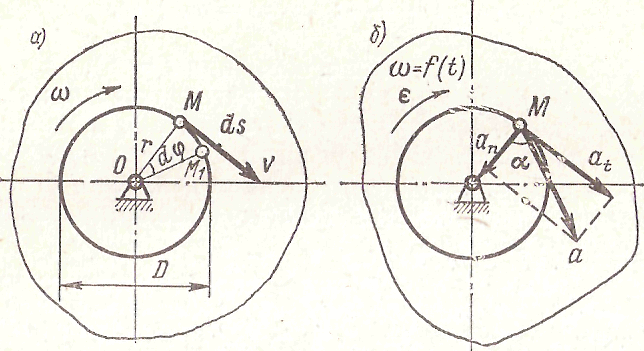 v = ds/dt = d(rφ)/dt = r* dφ/dt = rω 11
v = ds/dt = d(rφ)/dt = r* dφ/dt = rω 11 r =
r = 
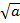 2t +a 2n = √1,122 + 102 = √1,25 + 100 = 10м/с2
2t +a 2n = √1,122 + 102 = √1,25 + 100 = 10м/с2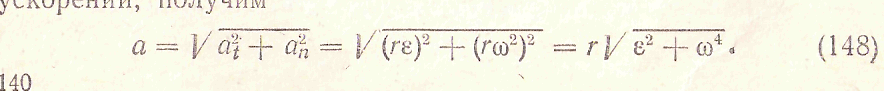

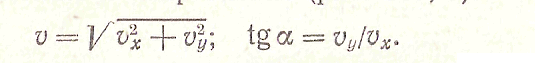 Если известны проекции скорости на оси координат, можно определить ее значение и направление:
Если известны проекции скорости на оси координат, можно определить ее значение и направление: