

Мы поможем в написании ваших работ!
ЗНАЕТЕ ЛИ ВЫ?
|
Движение по окружности с постоянной по модулю скоростью
| А 1
| Период обращения тела, движущегося равномерно по окружности, увеличился в 2 раза. Частота обращения
| |
| 1) возросла в 2 раза
| 2) уменьшилась в 2 раза
| |
| 3) возросла в 4 раза
| 4) уменьшилась в 4 раза
| | А 2
| Материальная точка, двигаясь равномерно по окружности, за 3 с прошла четверть окружности. Определите частоту обращения точки
1)  2) 2)  3) 3)  4) 4) 
| | А 3
| Период равномерного движения материальной точки по окружности равен  , радиус окружности , радиус окружности  . Точка пройдёт по окружности путь, равный . Точка пройдёт по окружности путь, равный  , за время равное
1) 2 , за время равное
1) 2  2) 2) /2 3) /2 3)  4) 4) 
| | А 4
| Когда период вращения Земли вокруг своей оси самый короткий?
| |
| 1) Летом
| 2) Зимой
| |
| 3) Весной и осенью
| 4) Всегда одинаковый
| | А 5
| Период обращения Земли вокруг Солнца равен одному году, радиус орбиты Земли равен 150 млн. км. Скорость движения Земли по орбите примерно равна
1) 30 м/с 2) 30 км/с3) 150 км/с 4) 1800 км/с
| | А 6
| На кольцевой гонке два автомобиля движутся так, что всё время радиус движения второго автомобиля в 2 раза больше первого, а периоды движения равны. Отношение скоростей  равно …
1) 0,5 2) 23) равно …
1) 0,5 2) 23)  4) 4 4) 4
| | А 7
| По окружностям с радиусами R1 и R2 равномерно движутся две материальные точки со скоростями  и и  соответственно. Периоды их обращения одинаковы. Для данного случая справедливо равенство
1) соответственно. Периоды их обращения одинаковы. Для данного случая справедливо равенство
1)  2) 2)  3) 3)  4) 4) 
| | А 8
| Две материальные точки движутся по окружностям радиусами 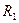 и и  с одинаковыми по модулю скоростями. Их периоды обращения по окружностям связаны соотношением
1) с одинаковыми по модулю скоростями. Их периоды обращения по окружностям связаны соотношением
1)  2) 2)  3) 3)  4) 4) 
| | А 9
| По окружностям с радиусами R1 и R2 равномерно движутся две материальные точки со скоростями  и и  соответственно. Частоты их обращения одинаковы. Для данного случая справедливо равенство
1) соответственно. Частоты их обращения одинаковы. Для данного случая справедливо равенство
1)  2) 2)  3) 3)  4) 4)
|
| А 10
| По окружностям одинакового радиуса равномерно движутся две материальные точки со скоростями  и и  соответственно. Частота обращения первой точки в 2 раза меньше частоты обращения второй. Для данного случая справедливо равенство
1) соответственно. Частота обращения первой точки в 2 раза меньше частоты обращения второй. Для данного случая справедливо равенство
1) 2) 2)  3) 3)  4) 4) 
| | А 11
| По окружностям одинакового радиуса равномерно движутся две материальные точки со скоростями  и и  соответственно. Частота обращения первой точки в 2 раза больше частоты обращения второй. Для данного случая справедливо равенство
1) соответственно. Частота обращения первой точки в 2 раза больше частоты обращения второй. Для данного случая справедливо равенство
1)  2) 2)  3) 3) 4) 4) 
| | А 12
| Две материальные точки равномерно движутся по окружностям одинакового радиуса, при этом линейная скорость первой точки в 2 раза меньше линейной скорости второй точки. Частоты обращения точек по окружностям связаны соотношением:
1)  2) 2)  3) 3) 4) 4) 
| | А 13
| К боковой поверхности цилиндра, вращающегося вокруг своей оси, прижимают второй цилиндр с осью, параллельной оси первого, и радиусом, вдвое превосходящим радиус первого. При совместном вращении двух цилиндров без проскальзывания у них совпадают
1) периоды вращения
2) частоты вращения
3) линейные скорости точек на поверхности
4) центростремительные ускорения точек на поверхности
| |
| Две шестерни, сцепленные друг с другом, вращаются вокруг неподвижных осей. Большая шестерня радиусом 20 см делает 20 оборотов за 10 с. Сколько оборотов в секунду делает шестерня радиусом 10 см?
| |
| Две шестерни, сцепленные друг с другом, вращаются вокруг неподвижных осей. Большая шестерня радиусом 10 см делает 20 оборотов за 10 с, а частота обращения меньшей шестерни равна 5 Гц. Каков радиус меньшей шестерни? Ответ укажите в сантиметрах.
| |
| Две шестерни, сцепленные друг с другом, вращаются вокруг неподвижных осей. Отношение периодов вращения шестерен равно 3. Радиус меньшей шестерни равен 6 см. Каков радиус большей шестерни? Ответ укажите в сантиметрах.
| | А 17
| Диск радиусом 20 см равномерно вращается вокруг своей оси. Скорость точки, находящейся на расстоянии 15 см от центра диска, равна 1,5 м/с. Скорость крайних точек диска равна
1) 4 м/с 2) 0,2 м/с 3) 2 м/с4) 1,5 м/с
| | А 18
| При равномерном движении по окружности модуль вектора изменения скорости при перемещении из точки А в точку В (см. рисунок) равен
| 
| |
| 1) 0 2) 3) 3)  4) 4) 
| | А 19
| Вектор ускорения при равномерном движении точки по окружности
1) постоянен по модулю и по направлению
2) равен нулю
3) постоянен по модулю, но непрерывно изменяется по направлению
 4) постоянен по направлению, но непрерывно изменяется по модулю 4) постоянен по направлению, но непрерывно изменяется по модулю
| | А 20
| Автомобиль движется с постоянной по модулю скоростью по траектории, представленной на рисунке. В какой из указанных точек траектории центростремительное ускорение максимально?
|
| |
| 1) 1 2) 2 3) 34) Во всех точках одинаково
| | А 21
| Автомобиль движется по закруглению дороги радиусом 20 м с постоянной по модулю скоростью 10 м/с. Центростремительное ускорение автомобиля равно
1) 12,5 м/с2 2) 10м/с2 3) 5 м/с2 4) 4 м/с2
| | А 22
| Автомобиль движется по закруглению дороги радиусом 20 м с центростремительным ускорением 5 м/с2. Скорость автомобиля равна
1) 12,5 м/с 2) 10 м/с3) 5 м/с 4) 4 м/с
| | А 23
| Материальная точка движется по окружности с постоянной по модулю скоростью. Как изменится модуль её центростремительного ускорения, если скорость точки увеличить втрое?
| |
| 1) Увеличится в 3 раза
| 2) Увеличится в 9 раз
| |
| 3) Уменьшится в 3 раза
| 4) Уменьшится в 9 раз
| | А 24
| Материальная точка движется по окружности с постоянной по модулю скоростью. Как изменится модуль её центростремительного ускорения, если скорость точки увеличить в два раза?
| |
| 1) Не изменится
| 2) Увеличится в 4 раза
| |
| 3) Уменьшится в 2 раза
| 4) Уменьшится в 4 раза
|
| А 25
| Точка движется с постоянной по модулю скоростью  по окружности радиуса по окружности радиуса  . Как изменится центростремительное ускорение точки, если её скорость увеличить вдвое, а радиус окружности вдвое уменьшить? . Как изменится центростремительное ускорение точки, если её скорость увеличить вдвое, а радиус окружности вдвое уменьшить?
| | |
| 1) Уменьшится в 2 раза
| 2) Увеличится в 2 раза
| | |
| 3) Увеличится в 4 раза
| 4) Увеличится в 8 раз
| | | А 26
| Точка движется с постоянной по модулю скоростью  по окружности радиуса по окружности радиуса  . Как изменится центростремительное ускорение точки, если её скорость уменьшить в 2 раза, а радиус окружности в 2 раза увеличить? . Как изменится центростремительное ускорение точки, если её скорость уменьшить в 2 раза, а радиус окружности в 2 раза увеличить?
| | |
| 1) Уменьшится в 2 раза
| 2) Увеличится в 2 раза
| | |
| 3) Уменьшится в 8 раз
| 4) Не изменится
| | | А 27
| Две материальные точки движутся по окружностям радиусами 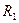 и и  , причём , причём  . При условии равенства линейных скоростей точек их центростремительные ускорения связаны соотношением
1) . При условии равенства линейных скоростей точек их центростремительные ускорения связаны соотношением
1)  2) 2)  3) 3)  4) 4) 
| | А 28
| Два спутника движутся по разным круговым орбитам вокруг Земли. Скорость первого из них в 2 раза больше, а радиус орбиты в 4 раза меньше, чем у второго. Центростремительное ускорение первого спутника  , а второго - , а второго -  . Чему равно отношение . Чему равно отношение  ?
1) 1 2) 2 3) 4 4) 16 ?
1) 1 2) 2 3) 4 4) 16
| | | В 29
| Материальная точка движется с постоянной скоростью по окружности радиусом  . Как изменятся перечисленные в первом столбце физические величины, если скорость точки увеличится? . Как изменятся перечисленные в первом столбце физические величины, если скорость точки увеличится?
| ФИЗИЧЕСКИЕ ВЕЛИЧИНЫ
| ИХ ИЗМЕНЕНИЕ
| | А) Угловая скорость
| 1) увеличится
| | Б) Центростремительное ускорение
| 2) уменьшится
| | В) Период обращения по окружности
| 3) не изменится
| | | | А 30
| Шарик движется по окружности радиусом  с угловой скоростью с угловой скоростью  . Как изменится центростремительное ускорение, если угловую скорость увеличить в 2 раза? . Как изменится центростремительное ускорение, если угловую скорость увеличить в 2 раза?
| | |
| 1) Увеличится в 2 раза 2) Уменьшится в 4 раза
3) Увеличится в 4 раза 4) Не изменится
| | | А 31
| Шарик движется по окружности радиусом  с угловой скоростью с угловой скоростью  . Как изменится центростремительное ускорение, если угловую скорость уменьшить в 2 раза? . Как изменится центростремительное ускорение, если угловую скорость уменьшить в 2 раза?
| | |
| 1) Увеличится в 2 раза 2) Уменьшится в 4 раза
3) Увеличится в 4 раза 4) Не изменится
| |
| А 32
| Тело движется по окружности с периодом обращения  . Как изменится центростремительное ускорение, если период обращения увеличить в 2 раза? . Как изменится центростремительное ускорение, если период обращения увеличить в 2 раза?
| |
| 1) Увеличится в 2 раза 2) Уменьшится в 2 раза
3) Увеличится в 4 раза 4) Уменьшится в 4 раза
| | А 33
| Тело движется по окружности с периодом обращения  . Как изменится центростремительное ускорение, если период обращения уменьшить в 2 раза? . Как изменится центростремительное ускорение, если период обращения уменьшить в 2 раза?
| |
| 1) Увеличится в 2 раза 2) Уменьшится в 2 раза
3) Увеличится в 4 раза 4) Уменьшится в 4 раза
| |
| Рассчитайте центростремительное ускорение льва, спящего на экваторе, в системе отсчёта, две оси координат которой лежат в плоскости экватора и направлены на неподвижные звёзды, а начало координат совпадает с центром Земли. Ответ округлите до двух значащих цифр. Радиус Земли 6400 км, а период вращения вокруг оси равен 1 суткам.
|
|



 2)
2)  3)
3)  4)
4) 
 , радиус окружности
, радиус окружности  . Точка пройдёт по окружности путь, равный
. Точка пройдёт по окружности путь, равный  , за время равное
1) 2
, за время равное
1) 2  4)
4) 
 равно …
1) 0,5 2) 23)
равно …
1) 0,5 2) 23)  4) 4
4) 4
 и
и  соответственно. Периоды их обращения одинаковы. Для данного случая справедливо равенство
1)
соответственно. Периоды их обращения одинаковы. Для данного случая справедливо равенство
1)  2)
2)  3)
3)  4)
4) 
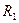 и
и  с одинаковыми по модулю скоростями. Их периоды обращения по окружностям связаны соотношением
1)
с одинаковыми по модулю скоростями. Их периоды обращения по окружностям связаны соотношением
1)  2)
2)  3)
3)  4)
4) 
 2)
2)  3)
3)  4)
4) 
 2)
2)  3)
3)
 2)
2)  3)
3) 4)
4) 


 3)
3)  4)
4) 
 4) постоянен по направлению, но непрерывно изменяется по модулю
4) постоянен по направлению, но непрерывно изменяется по модулю
 , причём
, причём  2)
2)  3)
3)  4)
4) 
 , а второго -
, а второго -  . Чему равно отношение
. Чему равно отношение  ?
1) 1 2) 2 3) 4 4) 16
?
1) 1 2) 2 3) 4 4) 16
 . Как изменится центростремительное ускорение, если угловую скорость увеличить в 2 раза?
. Как изменится центростремительное ускорение, если угловую скорость увеличить в 2 раза?



