
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Эволюция вращения твердого тела в переменных андуайеСодержание книги
Поиск на нашем сайте
Пусть движение симметричного твердого тела подвержено возмущениям двух типов: либо в выражении функции Гамильтона появляются малые добавки
либо на тело действует момент сил сопротивления, элементарная работа которого на возможных перемещениях равна
Здесь Канонические уравнения в переменных Андуайе, соответствующие возмущению
Хотя в системе имеются две быстрые переменные Во втором случае выразим скалярное произведение
Канонические уравнения в этом случае принимают вид
Из канонических уравнений (2) следует закон сохранения проекций вектора момента количеств движения на ось симметрии тела В третьем случае, когда возмущения являются силами сопротивления, элементарная работа, определенная выше, представляется в виде
Далее найдем
Согласно уравнениям (3) скорости угловых переменных не претерпевают изменений. Переменная
решение которых запишем в виде
Вращение тела под действием диссипативных сил замедляется, и его угловая скорость стремиться к нулю. Углы
ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА ВОКРУГ НЕПОДВИЖНОЙ ТОЧКИ С НЕГОЛОНОМНОЙ СВЯЗЬЮ (ЗАДАЧА Г.К.СУСЛОВА)
Пусть система координат
Здесь
Рис. 1 Динамические уравнения Эйлера движения твердого тела с неподвижной точкой имеют вид
Здесь
В явном виде соотношение (3) с учетом равенства нулю проекции угловой скорости тела
Уравнение (4) является уравнением эллипса на плоскости
Стационарные решения уравнений (5), когда их правые части обращаются в нуль, соответствуют перманентным вращениям вокруг оси, лежащей в плоскости
В дальнейшем угловая скорость не меняется в силу уравнений (5). Существует вырожденный случай, когда центробежные моменты инерции Исследуем устойчивость стационарных точек уравнений (5), используя уравнения в вариациях. Пусть
Характеристическое уравнение линейной системы дифференциальных уравнений с постоянными коэффициентами представляется в форме
Характеристическое уравнение (8) имеет один нулевой корень, который возникает как следствие существования интеграла энергии. Второй действительный корень является линейной комбинацией начальных значений проекций угловых скоростей
Первому интегралу (4) удовлетворяют две пары начальных условий
Рис. 2
Эллипс является множеством точек, на котором выполняется условие (4). Если начальные условия движения выбрать на эллипсе вблизи точки Найдем решение уравнений (5). Сделаем замену переменных
при которой интеграл энергии (4) превращается в тождество при любом
Уравнение (11) с разделяющимися переменными представим в форме
и далее найдем
где Отметим, что углы Эйлера, определяющие ориентацию твердого тела, удовлетворяют системе уравнений, полученной из кинематических уравнений Эйлера
в которой функции времени Литература: Суслов Г.К. Теоретическая механика. ОГИЗ. М.-Л. 1946. 655 с.
|
||||
|
Последнее изменение этой страницы: 2016-08-10; просмотров: 320; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.147.75.217 (0.007 с.) |



 – постоянные величины,
– постоянные величины,  – малый параметр,
– малый параметр,  – орты соответствующих осей. Гамильтониан
– орты соответствующих осей. Гамильтониан  соответствует несимметричному твердому телу в случае Эйлера с малым различием между главными моментами инерции
соответствует несимметричному твердому телу в случае Эйлера с малым различием между главными моментами инерции  и
и  . Гамильтониан
. Гамильтониан  определяет возмущения, соответствующие случаю Лагранжа при малой величине момента силы тяжести. Рассмотрим влияние каждого из этих возмущений на движение тела вокруг неподвижной точки. Напомним, что невозмущенное движение является регулярной прецессией.
определяет возмущения, соответствующие случаю Лагранжа при малой величине момента силы тяжести. Рассмотрим влияние каждого из этих возмущений на движение тела вокруг неподвижной точки. Напомним, что невозмущенное движение является регулярной прецессией. , имеют вид
, имеют вид (1)
(1) и
и  , правые части полученных уравнений зависят только от одной быстрой переменной
, правые части полученных уравнений зависят только от одной быстрой переменной  остаются постоянными. Переменная
остаются постоянными. Переменная  получает в первом приближении по малому параметру
получает в первом приближении по малому параметру  .
. через канонические переменные Андуайе. Имеем
через канонические переменные Андуайе. Имеем
 (2)
(2) и на вертикальную ось
и на вертикальную ось 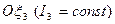 – первые интегралы в случае Лагранжа. Правые части уравнений (2) зависят от одной быстрой переменной
– первые интегралы в случае Лагранжа. Правые части уравнений (2) зависят от одной быстрой переменной  получает малое периодическое возмущение и в среднем остается равной своему невозмущенному значению, быстрые угловые переменные
получает малое периодическое возмущение и в среднем остается равной своему невозмущенному значению, быстрые угловые переменные  получают поправки в частоты
получают поправки в частоты  , а медленная угловая переменная
, а медленная угловая переменная  в среднем изменяется с малой угловой скоростью
в среднем изменяется с малой угловой скоростью  . Полученное усредненное движение соответствует медленно эволюционирующей регулярной прецессии тела, когда ось симметрии тела описывает круговой конус с постоянной угловой скоростью, вращаясь вокруг вектора момента количеств движения в невозмущенном движении, а ось конуса в свою очередь описывает с малой угловой скоростью другой круговой конус с вертикальной осью.
. Полученное усредненное движение соответствует медленно эволюционирующей регулярной прецессии тела, когда ось симметрии тела описывает круговой конус с постоянной угловой скоростью, вращаясь вокруг вектора момента количеств движения в невозмущенном движении, а ось конуса в свою очередь описывает с малой угловой скоростью другой круговой конус с вертикальной осью.

 Обобщенные силы равны коэффициентам при соответствующих вариациях
Обобщенные силы равны коэффициентам при соответствующих вариациях Правые части обобщенных сил зависят от одной быстрой переменной
Правые части обобщенных сил зависят от одной быстрой переменной  (3)
(3) . Обозначая
. Обозначая  , представим второе и третье уравнения системы (3) в виде
, представим второе и третье уравнения системы (3) в виде

 не изменяются, и остается постоянным направление вектора момента количеств движения
не изменяются, и остается постоянным направление вектора момента количеств движения  .
. неподвижна, а система координат
неподвижна, а система координат  связана с твердым телом. На теле в точке
связана с твердым телом. На теле в точке  на оси, лежащей в плоскости
на оси, лежащей в плоскости  , закреплен конек, лезвие которого направлено вдоль оси
, закреплен конек, лезвие которого направлено вдоль оси  и который скользит по неподвижной сфере с центром в точке
и который скользит по неподвижной сфере с центром в точке  (рис.1). Пусть вектор
(рис.1). Пусть вектор  , где
, где  – орт оси
– орт оси  . Скорость точки
. Скорость точки  (1)
(1) – угловая скорость твердого тела. Тело вращается вокруг неподвижной точки по инерции. На движение тела наложена неголономная связь (1). В точке контакта конька с неподвижной сферой на тело действует реакция неголономной связи – сила, направленная по оси с направляющим вектором
– угловая скорость твердого тела. Тело вращается вокруг неподвижной точки по инерции. На движение тела наложена неголономная связь (1). В точке контакта конька с неподвижной сферой на тело действует реакция неголономной связи – сила, направленная по оси с направляющим вектором 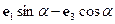 . Момент этой силы относительно неподвижной точки
. Момент этой силы относительно неподвижной точки  .
.
 (2)
(2) – тензор инерции тела относительно системы координат
– тензор инерции тела относительно системы координат  достигается соответствующим выбором угла
достигается соответствующим выбором угла  . Умножим уравнение (2) скалярно на вектор угловой скорости
. Умножим уравнение (2) скалярно на вектор угловой скорости  и получим первый интеграл – закон сохранения кинетической энергии
и получим первый интеграл – закон сохранения кинетической энергии (3)
(3) примет вид
примет вид (4)
(4) . Уравнения движения (2) в проекциях на оси
. Уравнения движения (2) в проекциях на оси  и
и  имеют вид
имеют вид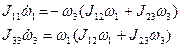 (5)
(5) (6)
(6) . В этом случае любая ось, проходящая через начало координат и лежащая в плоскости
. В этом случае любая ось, проходящая через начало координат и лежащая в плоскости  . Уравнения в вариациях имеют вид
. Уравнения в вариациях имеют вид (7)
(7) (8)
(8)
 (9)
(9) , которым соответствуют перманентные вращения вокруг одной и той же оси, но в разных направлениях. В зависимости от знака соответствующего корня (9) одно из этих вращений оказывается устойчивым, а второе – неустойчивым. Общая картина движения на плоскости переменных
, которым соответствуют перманентные вращения вокруг одной и той же оси, но в разных направлениях. В зависимости от знака соответствующего корня (9) одно из этих вращений оказывается устойчивым, а второе – неустойчивым. Общая картина движения на плоскости переменных  представлена на рисунке 2.
представлена на рисунке 2.
 (10)
(10) . Первое уравнение системы (5) примет вид
. Первое уравнение системы (5) примет вид (11)
(11)
 (12)
(12)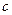 – произвольная постоянная. Правая часть уравнения (12) стремится к бесконечности, когда
– произвольная постоянная. Правая часть уравнения (12) стремится к бесконечности, когда  стремится к бесконечности. Следовательно,
стремится к бесконечности. Следовательно,  или
или  , когда время стремится к бесконечности. Знаки плюс или минус соответствуют двум возможным сценариям движения, отмеченным выше, когда движение тела стремится к стационарному вращению вокруг прямой
, когда время стремится к бесконечности. Знаки плюс или минус соответствуют двум возможным сценариям движения, отмеченным выше, когда движение тела стремится к стационарному вращению вокруг прямой  . В стационарном движении конек описывает окружность на сфере радиуса
. В стационарном движении конек описывает окружность на сфере радиуса 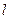 . Центр окружности лежит на оси вращения твердого тела.
. Центр окружности лежит на оси вращения твердого тела.
 определяются из соотношений (10), (12).
определяются из соотношений (10), (12).


