
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Равновесие и малые колебания нити в однородном поле силы тяжестиСодержание книги
Поиск на нашем сайте
Пусть концы нити с постоянной линейной плотностью
Из второго и третьего уравнений системы (14) найдем
Учитывая граничные условия в соотношениях (14), найдем постоянные
Интегрируя последнее равенство, найдем форму нити в положении равновесия
Постоянные интегрирования
и условия равенства длины нити
Таким образом, нить, закрепленная в двух концах, имеет форму, описываемую гиперболическим косинусом, и называется цепной линией. Рассмотрим теперь задачу о равновесии тяжелой нити и ее малых колебаниях, в случае, когда один ее конец закреплен в начале координат, а второй конец свободен. Используем независимые координаты Лагранжа
Поскольку согласно (9) Отсюда следует, что
Здесь Среди положений равновесия существует одно, когда натяжение нити положительно. Это происходит при
В положении равновесия
Согласно теореме Лагранжа об устойчивости положения равновесия положение равновесия нити, весящей по вертикали, устойчиво, так как вторая вариация функционала потенциальной энергии положительна, и потенциальная энергия имеет изолированный минимум в этом положении равновесия. Рассмотрим малые колебания нити около этого положения равновесия, используя уравнения движения в декартовых координатах (6). Имеем
Сделаем замену переменных
Из третьего уравнения следует, что
Уравнение (20) было получено Д.Бернулли при описании малых колебаний подвешенной цепи и им же было получено решения в виде рядов. В дальнейшем это уравнение изучал Л.Эйлер и Ф.Бессель. Решение уравнения (20) будем искать в виде
Первое уравнение системы (21) имеет решение
Функция Бесселя нулевого порядка
Решение задачи о малых колебаниях нити около положения равновесия записывается в форме
где постоянные
|
||||
|
Последнее изменение этой страницы: 2016-08-10; просмотров: 468; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.41 (0.01 с.) |

 закреплены, и
закреплены, и  . Конфигурация нити рассматривается относительно инерциальной системы координат
. Конфигурация нити рассматривается относительно инерциальной системы координат 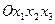 ,
,  - орты ее осей, и по оси
- орты ее осей, и по оси  действует поле силы тяжести
действует поле силы тяжести  . Будем считать, что длина нити превосходит расстояние между ее закрепленными концами. В случае равновесия система уравнений (6) и граничные условия представляются в виде
. Будем считать, что длина нити превосходит расстояние между ее закрепленными концами. В случае равновесия система уравнений (6) и граничные условия представляются в виде (14)
(14) (15)
(15) . Последнее означает, что нить будет находиться в плоскости
. Последнее означает, что нить будет находиться в плоскости  . Представим первые уравнения систем (14) и (15) в дифференциальной форме, учитывая условие нерастяжимости нити
. Представим первые уравнения систем (14) и (15) в дифференциальной форме, учитывая условие нерастяжимости нити 
 (16) Согласно первому уравнению (15) производная
(16) Согласно первому уравнению (15) производная  не меняет знак на всем интервале изменения параметра
не меняет знак на всем интервале изменения параметра  , так как натяжение нити положительно. Если принять в соответствующем граничном условии (14) координату конца нити
, так как натяжение нити положительно. Если принять в соответствующем граничном условии (14) координату конца нити  , то константа
, то константа  и производная
и производная  монотонно возрастает, и координату
монотонно возрастает, и координату 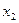 можно принять в качестве параметра при определении формы нити. В этом случае последнее соотношение в (16) примет вид
можно принять в качестве параметра при определении формы нити. В этом случае последнее соотношение в (16) примет вид

 определяются из граничных условий
определяются из граничных условий

 . В случае равновесия нити в уравнениях (13) следует положить силовое поле внешних сил равным
. В случае равновесия нити в уравнениях (13) следует положить силовое поле внешних сил равным  и поле ускорений равным нулю. В результате уравнения (13) примут вид
и поле ускорений равным нулю. В результате уравнения (13) примут вид (17)
(17) , то из уравнений (17) получим систему
, то из уравнений (17) получим систему 
 . Поскольку угол
. Поскольку угол  в сферической системе координат изменяется от нуля до
в сферической системе координат изменяется от нуля до  , то целое число
, то целое число  и
и  . В результате найдем функции, определяющие форму нити в положениях равновесия
. В результате найдем функции, определяющие форму нити в положениях равновесия
 - борелевское множество, получаемое путем конечного или счетного разбиения интервала
- борелевское множество, получаемое путем конечного или счетного разбиения интервала  на интервалы, и дальнейшего выбрасывания произвольной конечного или счетного множества в полученной системе интервалов. Подобная структура функции
на интервалы, и дальнейшего выбрасывания произвольной конечного или счетного множества в полученной системе интервалов. Подобная структура функции  связана с тем, что она задается по модулю
связана с тем, что она задается по модулю  и может принимать два различных значения 0 или
и может принимать два различных значения 0 или  принимает только одно значение. Все возможные положения равновесия нить представляются нитью сложенной конечное или счетное число раз вдоль оси
принимает только одно значение. Все возможные положения равновесия нить представляются нитью сложенной конечное или счетное число раз вдоль оси  , когда нить висит вдоль вертикальной оси. Исследуем устойчивость этого положения равновесия. Потенциальная энергия нити и ее вариации равны
, когда нить висит вдоль вертикальной оси. Исследуем устойчивость этого положения равновесия. Потенциальная энергия нити и ее вариации равны

 (18)
(18) . Значения
. Значения  соответствуют положению равновесия вертикально висящей нити. Считая возмущения и их производные малыми величинами и сохраняя только члены первого порядка малости, представим уравнения системы (18) и условие нерастяжимости нити в виде
соответствуют положению равновесия вертикально висящей нити. Считая возмущения и их производные малыми величинами и сохраняя только члены первого порядка малости, представим уравнения системы (18) и условие нерастяжимости нити в виде (19)
(19) , а из второго -
, а из второго -  . Первое уравнение после замены переменной
. Первое уравнение после замены переменной  представляется в форме
представляется в форме (20)
(20)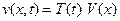 . Далее получим
. Далее получим (21)
(21) и определяет гармонический характер колебаний собственных форм нити, которые являются решениями второго уравнения
и определяет гармонический характер колебаний собственных форм нити, которые являются решениями второго уравнения
 описывает нормальную форму нити. Ее вид подобен графику косинусойды, амплитуда колебаний которой стремится к нулю при
описывает нормальную форму нити. Ее вид подобен графику косинусойды, амплитуда колебаний которой стремится к нулю при  стремящемся к бесконечности. Отметим ряд свойств функции Бесселя. Во-первых,
стремящемся к бесконечности. Отметим ряд свойств функции Бесселя. Во-первых,  , во-вторых, ряд, определяющий функцию Бесселя, сходится равномерно при любом
, во-вторых, ряд, определяющий функцию Бесселя, сходится равномерно при любом  имеет счетное число действительных корней
имеет счетное число действительных корней 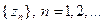 , образующих последовательность, стремящуюся к бесконечности. Учитывая граничное условие в (21), получим спектр собственных частот
, образующих последовательность, стремящуюся к бесконечности. Учитывая граничное условие в (21), получим спектр собственных частот  . При этом соответствующая нормальная собственная форма малых колебаний нити представится функцией Бесселя, заданной на интервале изменения
. При этом соответствующая нормальная собственная форма малых колебаний нити представится функцией Бесселя, заданной на интервале изменения  от нуля до
от нуля до 
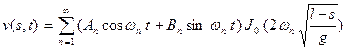
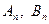 определяются из начальных условий
определяются из начальных условий  .
.


