
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Уравнения движения гибкой нерастяжимой нити в декартовых координатах, в проекциях на оси естественного трехгранника и в независимых координатахСодержание книги
Поиск на нашем сайте
О. Механическая система Мера, определяющая распределение массы вдоль длины нити, задается соотношением
Условие нерастяжимости нити записывается в форме
Дифференцируя правую и левую части соотношения (1) частным образом по
Условие (2) является двусторонней голономной связью, наложенной на перемещения точек нити, а их возможные перемещения принадлежат функциональному пространству
Голономная связь (2) порождает поле реакций связи, которое будем считать идеальным (аксиома идеальных связей). Условие идеальности связей представляется в форме
Воспользуемся методом неопределенных множителей Лагранжа и получим соотношение
Здесь вариации
Полагая
Произвольная функция Принцип Д`Аламбера-Лагранжа после освобождения от всех связей представится в форме
Здесь
Система уравнений (6) в частных производных совместно с условием нерастяжимости нити (2) образуют полную систему уравнений, описывающих движение нити. Эта система аналогична уравнениям Лагранжа первого рода с неопределенными множителями. В данном случае роль неопределенного множителя играет функция В ряде случаев ставится задача статики - задача определения формы нити в положении равновесия, когда силовое поле внешних сил стационарно и стационарны граничные условия. Уравнение (6), представляется в виде системы дифференциальных уравнений с обыкновенными производными по натуральному параметру
Спроектируем его на оси естественного трехгранника, связанного с кривой, определяющей форму нити. Орты естественного трехгранника Френе задаются соотношениями
где
Уравнения (8) представляют систему обыкновенных дифференциальных уравнений в проекциях на оси естественного трехгранника, связанного с кривой, описывающей равновесие нити. При решении этих уравнений следует учитывать уравнение нерастяжимости нити (2) и граничные условия. Движение нерастяжимой нити можно описать с использованием независимых координат Лагранжа, определив конфигурацию нити соотношением
где Заметим, что гибкая нерастяжимая нить может быть получена как предельное состояние механической системы, состоящей из Процедуру составления уравнений Лагранжа второго рода рассмотрим для однородной нити постоянной плотности с одним закрепленным концом, полагая
Вариационный принцип Д`Аламбера-Лагранжа запишем в виде
где поле ускорений точек нити определяется равенством
В результате получим
Поскольку в интеграле (12) вариации
|
||||
|
Последнее изменение этой страницы: 2016-08-10; просмотров: 643; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.219.127.59 (0.01 с.) |


 называется гибкой нерастяжимой нитью, если в процессе движения остается неизменной длина ее любой части.
называется гибкой нерастяжимой нитью, если в процессе движения остается неизменной длина ее любой части. , где
, где  - натуральный параметр кривой, определяющей конфигурацию нити, а
- натуральный параметр кривой, определяющей конфигурацию нити, а 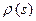 - ее линейная плотность. Движение нити относительно инерциальной системы координат
- ее линейная плотность. Движение нити относительно инерциальной системы координат 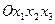 представим в виде
представим в виде
 (1)
(1) , получим условие нерастяжимости нити
, получим условие нерастяжимости нити (2)
(2) и удовлетворяют условию
и удовлетворяют условию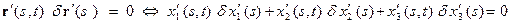 (3)
(3)
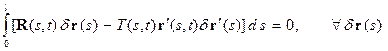
 произвольны. Интегрируя второе слагаемое подынтегрального выражения по частям, найдем
произвольны. Интегрируя второе слагаемое подынтегрального выражения по частям, найдем
 , получим согласно основной лемме вариационного исчисления равенство
, получим согласно основной лемме вариационного исчисления равенство (4)
(4) в соотношениях (4) имеет смысл натяжения нити в точке с координатой
в соотношениях (4) имеет смысл натяжения нити в точке с координатой  (5)
(5) - поле внешних массовых сил и две внешние силы, приложенные к концам нити. Эти силы могут быть внешними, если соответствующий конец нити свободен, или реакциями связей, если один или оба конца нити закреплены. В любом случае векторное поле возможных перемещений точек нити в соотношении (5) произвольно. Если один или оба конца нити закреплены, то соответствующие возможные перемещения в этих точках полагаются равными нулю (дополнительные голономные связи). Интегрируя по частям выражение, содержащее частную производную от вектора возможных перемещений, под знаком интеграла в равенстве (5) и учитывая произвольность поля возможных перемещений, получим уравнения движения нити и граничные условия
- поле внешних массовых сил и две внешние силы, приложенные к концам нити. Эти силы могут быть внешними, если соответствующий конец нити свободен, или реакциями связей, если один или оба конца нити закреплены. В любом случае векторное поле возможных перемещений точек нити в соотношении (5) произвольно. Если один или оба конца нити закреплены, то соответствующие возможные перемещения в этих точках полагаются равными нулю (дополнительные голономные связи). Интегрируя по частям выражение, содержащее частную производную от вектора возможных перемещений, под знаком интеграла в равенстве (5) и учитывая произвольность поля возможных перемещений, получим уравнения движения нити и граничные условия (6)
(6) , имеющая смысл натяжения нити и подлежащая определению в процессе решения задачи о движении нити. Уравнения (6) содержат граничные условия, соответствующие нити со свободными концами. Если один из концов нити закреплен или задано его движение (голономная связь), то соответствующее граничное условие следует заменить голономной связью, например,
, имеющая смысл натяжения нити и подлежащая определению в процессе решения задачи о движении нити. Уравнения (6) содержат граничные условия, соответствующие нити со свободными концами. Если один из концов нити закреплен или задано его движение (голономная связь), то соответствующее граничное условие следует заменить голономной связью, например,  .
. (7)
(7)
 - кривизна нити. Уравнение (7) перепишем в виде
- кривизна нити. Уравнение (7) перепишем в виде (8)
(8) (9)
(9) - радиус-вектор одного конца нити,
- радиус-вектор одного конца нити,  - единичный вектор касательной к кривой, описывающей форму нити и углы сферической системы координат, определяющие проекции вектора
- единичный вектор касательной к кривой, описывающей форму нити и углы сферической системы координат, определяющие проекции вектора 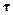 на оси неподвижной системы координат. Независимыми координатами Лагранжа являются вектор
на оси неподвижной системы координат. Независимыми координатами Лагранжа являются вектор  и две функции
и две функции  , первая из которых принимает значения от нуля до
, первая из которых принимает значения от нуля до  , а вторая задана по модулю
, а вторая задана по модулю  . Для определения непрерывной линии, задающей конфигурацию нити, достаточно, чтобы эти функции были суммируемыми по
. Для определения непрерывной линии, задающей конфигурацию нити, достаточно, чтобы эти функции были суммируемыми по  . В частности, эти функции могут иметь счетное число разрывов, которым будут соответствовать угловые точки перегиба нити.
. В частности, эти функции могут иметь счетное число разрывов, которым будут соответствовать угловые точки перегиба нити.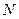 однородных стержней одинаковой длины соединенных сферическим шарнирами, при условии, что количество стержней стремится к бесконечности, суммарная длина всех стержней остается постоянной, а максимум длинны всех стержней стремится к нулю. Эта процедура может быть реализована путем деления пополам на каждом шаге всех стержней с добавлением в точках раздела сферических шарниров. Ясно, что в такой модели и ее предельном варианте реакции в стержнях и натяжение нити могут быть и отрицательными.
однородных стержней одинаковой длины соединенных сферическим шарнирами, при условии, что количество стержней стремится к бесконечности, суммарная длина всех стержней остается постоянной, а максимум длинны всех стержней стремится к нулю. Эта процедура может быть реализована путем деления пополам на каждом шаге всех стержней с добавлением в точках раздела сферических шарниров. Ясно, что в такой модели и ее предельном варианте реакции в стержнях и натяжение нити могут быть и отрицательными. . Скорости и возможные перемещения точек нити определяются по правилу
. Скорости и возможные перемещения точек нити определяются по правилу (10)
(10) (11)
(11) Преобразуем подынтегральное выражение в (11), используя процедуру интегрирования по частям и полагая
Преобразуем подынтегральное выражение в (11), используя процедуру интегрирования по частям и полагая
 (12)
(12) произвольны, то коэффициенты при них согласно основной лемме вариационного исчисления должны быть равны нулю. В результате получим два интегро-дифференциальных уравнения Лагранжа второго рода
произвольны, то коэффициенты при них согласно основной лемме вариационного исчисления должны быть равны нулю. В результате получим два интегро-дифференциальных уравнения Лагранжа второго рода (13)
(13)


