
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Вращение вокруг неподвижной точки и оси.Содержание книги
Поиск на нашем сайте
О. Твердым телом переменного состава называется множество точек переменного состава, расстояния между которыми не изменяются в процессе движения. Это означает, что система материальных точек определена на фиксированном множестве Система координат В каждой точке твердого тела определено поле активных сил
Теорема об изменении количества движения системы с учетом соотношений (17) примет вид
Аналогичным образом получим теорему об изменении момента количеств движения относительно неподвижной точки
Пусть твердое тело вращается вокруг неподвижной точки
Здесь
Объединяя подобные члены, получим векторное уравнение
где Если тело переменного состава вращается относительно неподвижной оси
П. 7. Пусть тело переменного состава вращается вокруг неподвижной оси
Уравнение (21) принимает вид
Таким образом, определяется угловая скорость вращения тела переменного состава под действием постоянного момента реактивных сил Заметим, что система, рассмотренная выше, отличается от системы переменного состава во втором примере, так как в нем взаимные расстояния между точками системы изменяются со временем.
ЛИТЕРАТУРА 1. Маркеев А.П. Теоретическая механика. М.: Наука, 1990. 2. Голубев Ю.Ф. Основы теоретической механики. М.: Изд–во МГУ, 2000. 3. Поляков Н.Н., Зегжда С.А., Юшков М.П. Теоретическая механика. М.:Высшая школа, 2000. 4. Бухгольц Н.Н. Основной курс теоретической механики. Ч.2.М.: Наука, 1966. 5. Журавлев В.Ф. Основы теоретической механики. М.: Физматлит, 2001. 6. Лидов М.Л. Курс лекций по теоретической механике. М.: Физматлит, 2010. 7. Мещерский И.В. Сборник задач по теоретической механике. М.: Наука, 1975. 8. Пятниций Е.С., Трухан Н.М., Ханукаев Ю.И., Яковенко Г.Н. Сборник задач по аналитической механике. М.: Наука, Физматлит, 1996. 9. Новоселов В.С. Аналитическая механика систем с переменными массами. Л. ЛГУ 1969. 238 с. 10. Новоселов В.С. Некоторые вопросы механики переменных масс с учетом внутреннего движения частиц//Вестник ЛГУ. Серия математика, механика, астрономия. 1956. Вып. 19. С.100–113.
ДИНАМИКА НЕРАСТЯЖИМОЙ НИТИ
|
||||
|
Последнее изменение этой страницы: 2016-08-10; просмотров: 267; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.119.160.224 (0.007 с.) |

 , а ее мера зависит от времени, т.е.
, а ее мера зависит от времени, т.е.  и
и  . Изменение меры, определяющей массу соответствующего множества, происходит за счет присоединения и отделения материальных частиц.
. Изменение меры, определяющей массу соответствующего множества, происходит за счет присоединения и отделения материальных частиц. неподвижна, а система координат
неподвижна, а система координат  связана с твердым телом. Точка
связана с твердым телом. Точка  , вообще говоря, не является центром масс тела, так как в процессе изменения масс точек тела центр масс перемещается внутри тела. Зададим дифференциал меры в виде
, вообще говоря, не является центром масс тела, так как в процессе изменения масс точек тела центр масс перемещается внутри тела. Зададим дифференциал меры в виде  , где
, где  - радиус вектор точки твердого тела относительно системы координат
- радиус вектор точки твердого тела относительно системы координат  определяет увеличение плотности за счет присоединения материальных частиц к точкам твердого тела, а
определяет увеличение плотности за счет присоединения материальных частиц к точкам твердого тела, а  – уменьшение плотности за счет отделения материальных частиц.
– уменьшение плотности за счет отделения материальных частиц. и поле реакций связей
и поле реакций связей  , обеспечивающее постоянство расстояний между точками твердого тела переменного состава. Эти поля считаются заданными в неподвижной системе координат
, обеспечивающее постоянство расстояний между точками твердого тела переменного состава. Эти поля считаются заданными в неподвижной системе координат  (17)
(17)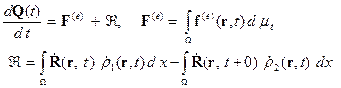 (18)
(18) (19)
(19) . Система координат
. Система координат 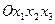 связана с твердым телом. Уравнения движения тела получим на основе теоремы об изменении момента количеств движения тела относительно неподвижной точки
связана с твердым телом. Уравнения движения тела получим на основе теоремы об изменении момента количеств движения тела относительно неподвижной точки  (20)
(20) – ортогональный оператор перехода от подвижной системы координат к неподвижной и угловая скорость твердого тела,
– ортогональный оператор перехода от подвижной системы координат к неподвижной и угловая скорость твердого тела,  ,
, 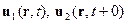 – поле внешних массовых сил и поля абсолютных скоростей материальных частиц, присоединяющихся к твердому телу и покидающих его, заданные в системе координат
– поле внешних массовых сил и поля абсолютных скоростей материальных частиц, присоединяющихся к твердому телу и покидающих его, заданные в системе координат 
 (21)
(21) – относительные скорости частиц присоединяющихся к твердому телу и покидающих его.
– относительные скорости частиц присоединяющихся к твердому телу и покидающих его. , то уравнение его движения получается путем проектирования уравнения (20) на эту ось с учетом равенства
, то уравнение его движения получается путем проектирования уравнения (20) на эту ось с учетом равенства  , где
, где  – угол между осями
– угол между осями  и
и  , а
, а  – орт оси
– орт оси  (22)
(22) , а отделение частиц твердого тела происходит в точке, характеризуемой вектором
, а отделение частиц твердого тела происходит в точке, характеризуемой вектором  с постоянной относительной скоростью
с постоянной относительной скоростью  . Изменение плотности в точке, где происходит отделение частиц, задается в виде
. Изменение плотности в точке, где происходит отделение частиц, задается в виде  , где
, где  – пространственная функция Дирака, а
– пространственная функция Дирака, а  – постоянный секундный расход массы. В этом случае имеем
– постоянный секундный расход массы. В этом случае имеем
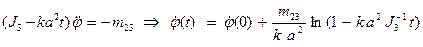
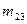 . Практическая реализация этой задачи получается путем установки реактивного двигателя на твердое тело, вращающееся вокруг неподвижной оси.
. Практическая реализация этой задачи получается путем установки реактивного двигателя на твердое тело, вращающееся вокруг неподвижной оси.


