
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Динамика системы переменного составаСодержание книги
Поиск на нашем сайте
Модели механических систем переменного состава используются для описания движений летательных аппаратов, нитей переменной длины, твердых тел, взаимодействующих со сплошной средой. Изучению динамики систем переменного состава в курсе теоретической механики уделяется, по мнению автора, недостаточное внимание и носит фрагментарный характер, поскольку этот раздел механики может быть представлен как в курсе теоретической механики, так и в курсе механики сплошной среды. В учебниках по теоретической механике теория систем переменного состава либо отсутствует, либо ее изложение не достаточно конструктивно. Традиционно этот раздел механики излагается в курсе классической теоретической механики [1–6] и присутствует в задачниках [7, 8]. Наибольшее внимание динамике систем переменного состава уделено в учебниках [1-3]. Теории систем переменного состава посвящены работы [9,10]. В последние годы возрос интерес к методам механики систем переменного состава в связи с моделированием контактных взаимодействий тел с учетом их деформаций и наличием смазки в контактных зонах. Отметим, что силовое взаимодействие в системах переменного состава в ряде случаев сводится к ударным явлениям, характеризуемым скачками поля скоростей точек, составляющих механическую систему. Если масса точек, испытывающих удары в данный момент времени равна нулю, то такое взаимодействие можно назвать «мягкими» ударами при условии, что это взаимодействие происходит в каждый момент времени. «Мягкие» удары описываются реактивными силами. Если происходит изменение состава системы при скачкообразном изменении массы системы в какой-то момент времени, например, падение метеорита на Землю, то такого рода взаимодействие описывается «жестким» ударом, при котором скачком изменяются скорости материальных точек положительной массы. Ниже представлено последовательное изложение динамики систем переменного состава и приведены примеры, поясняющие теоретические положения.
ОСНОВНЫЕ ПОНЯТИЯ И ТЕОРЕМЫ Рассмотрим механическую систему постоянного состава Пусть
Здесь О. Механической системой переменного состава называется система
Уравнение движения системы свободных материальных точек
где Определим количество движения системы переменного состава как вектор
Т.1. Производная по времени от количества движения системы переменного состава (3) равна сумме равнодействующей внешних сил
где Рассмотрим моменты времени
Рис.1
Функции
Здесь Замечание 1. Реактивная сила представленная в соотношениях (4) обращается в нуль, если Замечание 2. Скорости точек покидающих множество Замечание 3. Определим скорость центра масс системы переменного состава как вектор
Справедливы равенства
П.1. Рассмотрим прямолинейный полет реактивного самолета и пренебрежем изменением его массы за счет расхода топлива на достаточно малом интервале времени. Поскольку двигатели самолета засасывают воздух из атмосферы, а затем его выбрасывают со скоростью, большей скорости самолета, то возникает реактивная сила, разгоняющая самолет. Пусть самолет движется вдоль оси
Здесь
Аналогичным образом доказывается теорема об изменении момента количеств движения системы переменного состава
Т.2. Производная от момента количеств движения системы переменного состава относительно неподвижной точки
Приращение момента количеств движения за время
Далее с точностью до малых первого порядка относительно
Заменим в первом интеграле поле ускорений на поле сил согласно (2), разделим правую и левую части предыдущего равенства на П. 2. Пусть твердое тело вращается вокруг неподвижной оси
Здесь
где
Если момент внешних сил положить равным нулю, то угловая скорость тела определяется формулой
Все движения системы стремятся к стационарному вращению тела вокруг оси Рассмотрим случай физического маятника, когда момент внешних сил
Реактивный момент равен сумме постоянного момента и момента, линейных диссипативных сил. Докажем теорему об изменении кинетической энергии системы переменного состава. Т.3. Производная кинетической энергии системы переменного состава равна сумме мощностей активных и реактивных сил, т.е.
Согласно определению кинетическая энергия системы переменного состава и ее приращение равны
Представим приращение кинетической энергии в виде
Далее с точностью до малых первого порядка относительно
Заменим в соотношении (11) поле ускорений на поле активных сил согласно (2), разделим полученное равенство на П. 3. На горизонтальной плоскости расположена бесконечная система цилиндрических катков с осями, параллельными оси
где
Здесь
Время между двумя последовательными контактами переднего края доски с катком П. 4. Обобщим пример, рассмотренный выше, на случай, когда катки заменяются слоем сплошной среды, например, слоем жидкости или достаточно мелкого песка толщиной
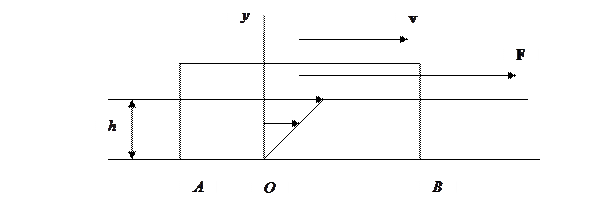
Рис. 2. ограниченной концами доски
где
Здесь
Если внешняя сила
где
получим скорость доски и закон ее движения
П. 5. Рассмотрим плоскую задачу о скольжении тела по «непрерывной» цепочке масс, связанных пружинками и демпферами с неподвижным основанием. Массы расположены вдоль оси
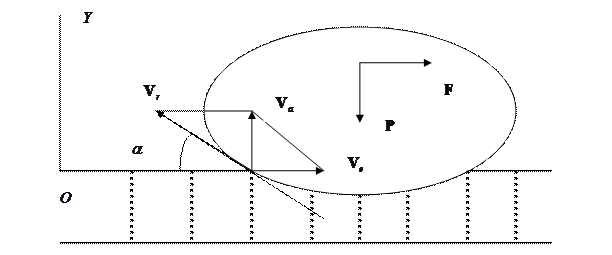
Рис. 3.
Применим теорему об изменении кинетической энергии к описанной выше системе переменного состава в случае стационарного движения тела. Имеем
Здесь
|
||||||||
|
Последнее изменение этой страницы: 2016-08-10; просмотров: 369; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.147.82.108 (0.008 с.) |

 и однопараметрическое семейство замкнутых областей
и однопараметрическое семейство замкнутых областей  ,
,  . Пусть
. Пусть  – масса материальных точек, образующих множество
– масса материальных точек, образующих множество  . Рассмотрим движение механической системы
. Рассмотрим движение механической системы  .
. – поле скоростей точек границы множества
– поле скоростей точек границы множества  , направленное по единичной внешней нормали
, направленное по единичной внешней нормали  к поверхности границы
к поверхности границы  . Тогда
. Тогда (1)
(1) – поверхностная мера, индуцированная пространственной мерой
– поверхностная мера, индуцированная пространственной мерой  . Например, в случае существования плотности
. Например, в случае существования плотности  справедливы равенства
справедливы равенства  , где
, где  – элемент площади поверхности
– элемент площади поверхности  , если
, если
 (2)
(2) – поле активных массовых сил. Уравнение (2) понимается в смысле равенства двух обобщенных функций, принадлежащих сопряженному пространству к пространству функций, непрерывных по времени и суммируемых по мере
– поле активных массовых сил. Уравнение (2) понимается в смысле равенства двух обобщенных функций, принадлежащих сопряженному пространству к пространству функций, непрерывных по времени и суммируемых по мере  на множестве
на множестве  .
. (3)
(3) , приложенных к точкам множества
, приложенных к точкам множества  , порождаемой изменением множества
, порождаемой изменением множества  (4)
(4) – часть границы
– часть границы  , а
, а  – часть границы
– часть границы  ,
,  – объемная плотность и элемент площади границы
– объемная плотность и элемент площади границы  .
. ,
,  и приращение количества движения системы переменного состава (3)
и приращение количества движения системы переменного состава (3)


 как функции времени предполагаются гладкими на множестве
как функции времени предполагаются гладкими на множестве  может иметь разрыва первого рода. Далее с точностью до малых порядка
может иметь разрыва первого рода. Далее с точностью до малых порядка  представим полученное приращение в виде
представим полученное приращение в виде (5)
(5)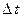 стремящимся к нулю. В результате получим равенство (4), если учесть, что интеграл от поля активных сил равен интегралу от внешних активных сил согласно третьему закону Ньютона.
стремящимся к нулю. В результате получим равенство (4), если учесть, что интеграл от поля активных сил равен интегралу от внешних активных сил согласно третьему закону Ньютона. . В этом случае система превращается в систему постоянного состава.
. В этом случае система превращается в систему постоянного состава.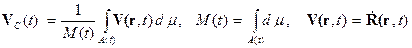
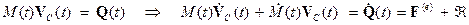 (6)
(6)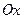 . Пусть
. Пусть 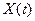 – координата его центра масс. Масса самолета
– координата его центра масс. Масса самолета 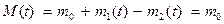 постоянна, а его количество движения равно
постоянна, а его количество движения равно 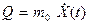 . Здесь
. Здесь 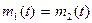 – массы воздуха, поступившего в двигатели из атмосферы, и масса воздуха, выброшенная из сопел двигателей. Уравнение (4) представляется в форме
– массы воздуха, поступившего в двигатели из атмосферы, и масса воздуха, выброшенная из сопел двигателей. Уравнение (4) представляется в форме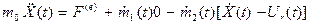 (7)
(7)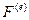 – сила сопротивления воздуха, приложенная к корпусу самолета,
– сила сопротивления воздуха, приложенная к корпусу самолета, 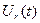 – скорость струи воздуха, выбрасываемой двигателями, относительно корпуса самолета. Уравнение (7) перепишем в виде
– скорость струи воздуха, выбрасываемой двигателями, относительно корпуса самолета. Уравнение (7) перепишем в виде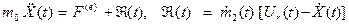
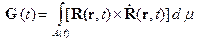 (8)
(8) (начала координат) равна сумме моментов внешних активных сил и моменту реактивных сил, т.е.
(начала координат) равна сумме моментов внешних активных сил и моменту реактивных сил, т.е.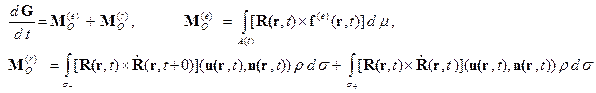 (9)
(9)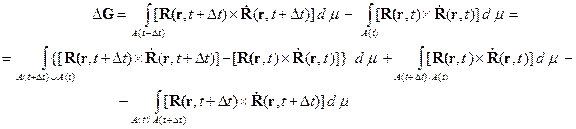
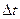 получим
получим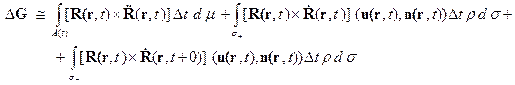
 . В теле имеется тонкий криволинейный канал
. В теле имеется тонкий криволинейный канал  , начало которого точка
, начало которого точка  лежит на оси
лежит на оси  – на поверхности тела. В системе координат
– на поверхности тела. В системе координат  , связанной с телом, уравнение канала задается в параметрическом виде
, связанной с телом, уравнение канала задается в параметрическом виде  , где
, где  – натуральный параметр. Вектор
– натуральный параметр. Вектор  – единичный вектор касательной к кривой
– единичный вектор касательной к кривой 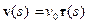 . Линейная плотность частиц равна
. Линейная плотность частиц равна 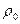 . Система переменного состава состоит из твердого тела и множества частиц, находящихся в канале
. Система переменного состава состоит из твердого тела и множества частиц, находящихся в канале 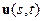 системы переменного состава отличны от нуля в концевых точках канала и соответственно равны
системы переменного состава отличны от нуля в концевых точках канала и соответственно равны 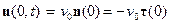 и
и 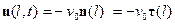 , поскольку внешние нормали в этих точках
, поскольку внешние нормали в этих точках 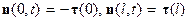 . Суммарная масса системы остается постоянной. Заметим, что постоянство модуля скорости частиц в канале обеспечивается за счет поля внутренних реакций связей. Запишем теорему об изменении момента количества движения системы относительно оси
. Суммарная масса системы остается постоянной. Заметим, что постоянство модуля скорости частиц в канале обеспечивается за счет поля внутренних реакций связей. Запишем теорему об изменении момента количества движения системы относительно оси 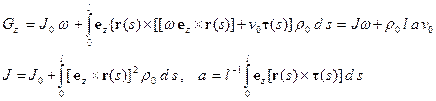
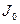 – момент инерции тела относительно оси
– момент инерции тела относительно оси 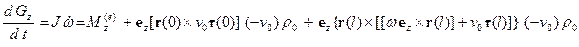
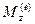 – момент внешних сил относительно оси
– момент внешних сил относительно оси  и
и 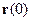 коллинеарные. В результате получим
коллинеарные. В результате получим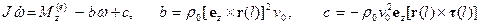
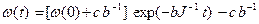
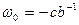 .
.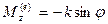 . Уравнение движения примет вид
. Уравнение движения примет вид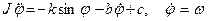
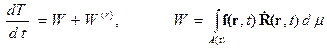 (10)
(10)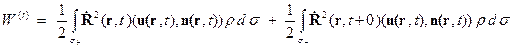
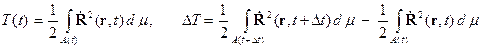
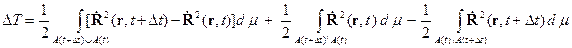
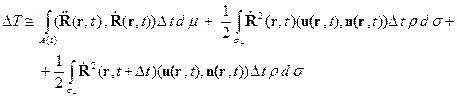 (11)
(11) . Масса каждого катка равна
. Масса каждого катка равна  ,
,  – радиус цилиндра,
– радиус цилиндра,  – момент инерции относительно оси цилиндра. Расстояние между осями покоящихся цилиндров равно
– момент инерции относительно оси цилиндра. Расстояние между осями покоящихся цилиндров равно  . По каткам движется доска вдоль оси
. По каткам движется доска вдоль оси  . Относительные скорости точек контакта катков с доской и дорогой равны нулю. В качестве системы переменного состава рассматривается доска и набор катков, контактирующих с ней. Состав системы меняется в дискретные моменты времени, когда новый передний каток соприкасается с краем доски, а каток на заднем краю доски прекращает контактировать с доской. В промежутке между этими событиями система сохраняет состав, а доска движется с постоянной скоростью, поскольку имеет место закон сохранения энергии. Непосредственно перед контактом с передним катком доска двигалась по
. Относительные скорости точек контакта катков с доской и дорогой равны нулю. В качестве системы переменного состава рассматривается доска и набор катков, контактирующих с ней. Состав системы меняется в дискретные моменты времени, когда новый передний каток соприкасается с краем доски, а каток на заднем краю доски прекращает контактировать с доской. В промежутке между этими событиями система сохраняет состав, а доска движется с постоянной скоростью, поскольку имеет место закон сохранения энергии. Непосредственно перед контактом с передним катком доска двигалась по  каткам, а кинетическая энергия системы равнялась
каткам, а кинетическая энергия системы равнялась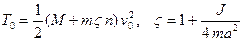
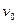 – начальная скорость доски. Процесс взаимодействия доски с катком будем описывать абсолютно неупругим ударом, в результате которого поле скоростей катка становится отличным от нуля. После того, как передний каток вошел в контакт с передним краем доски, а задний каток покинул систему переменного состава, система сохранила свою массу, но потеряла часть кинетической энергии за счет выхода из состава системы заднего катка. В результате получим равенство
– начальная скорость доски. Процесс взаимодействия доски с катком будем описывать абсолютно неупругим ударом, в результате которого поле скоростей катка становится отличным от нуля. После того, как передний каток вошел в контакт с передним краем доски, а задний каток покинул систему переменного состава, система сохранила свою массу, но потеряла часть кинетической энергии за счет выхода из состава системы заднего катка. В результате получим равенство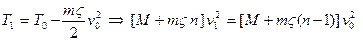
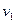 – скорость доски после контакта переднего катка с доской. Если произошло
– скорость доски после контакта переднего катка с доской. Если произошло  замен передних и задних катков, то скорость доски окажется равной
замен передних и задних катков, то скорость доски окажется равной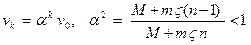
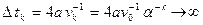 , а скорость
, а скорость 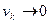 при
при 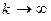 . Рассмотренный пример иллюстрирует ситуацию, когда в системе имеют место «жесткие» удары, а ее состав меняется в дискретные моменты времени.
. Рассмотренный пример иллюстрирует ситуацию, когда в системе имеют место «жесткие» удары, а ее состав меняется в дискретные моменты времени.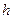 . Систему переменного состава образует доска и часть слоя сплошной среды,
. Систему переменного состава образует доска и часть слоя сплошной среды,
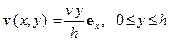 (12)
(12)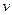 – скорость доски вдоль оси
– скорость доски вдоль оси 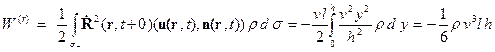 .
.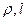 – плотность материала сплошной среды и ширина доски в направлении оси
– плотность материала сплошной среды и ширина доски в направлении оси 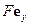 , то кинетическая энергия системы переменного состава постоянна, а мощность внешней силы
, то кинетическая энергия системы переменного состава постоянна, а мощность внешней силы 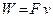 . Теорему об изменении кинетической энергии системы переменного состава запишем в форме
. Теорему об изменении кинетической энергии системы переменного состава запишем в форме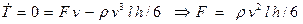
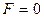 , то ускорение доски отрицательно. Кинетическая энергия системы и теорема об ее изменении примут вид
, то ускорение доски отрицательно. Кинетическая энергия системы и теорема об ее изменении примут вид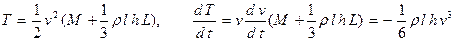
 – длина доски
– длина доски 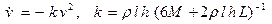

 . В стационарном поступательном движении тела со скоростью
. В стационарном поступательном движении тела со скоростью 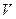 вдоль оси
вдоль оси 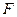 , направленная по оси
, направленная по оси 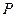 , обуславливающая перемещения масс вдоль оси
, обуславливающая перемещения масс вдоль оси 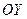 в зоне контакта тела с цепочкой масс. На рис.3 пружинки обозначены пунктирными линиями. В качестве системы переменного состава рассмотрим тело и множество масс, соприкасающихся с поверхностью тела. Масса системы не меняется, но состав системы переменен. На переднем фронте зоны контакта к системе присоединяются массы с нулевой абсолютной скоростью, а на заднем фронте – отделяются массы, абсолютные скорости которых направлены по оси
в зоне контакта тела с цепочкой масс. На рис.3 пружинки обозначены пунктирными линиями. В качестве системы переменного состава рассмотрим тело и множество масс, соприкасающихся с поверхностью тела. Масса системы не меняется, но состав системы переменен. На переднем фронте зоны контакта к системе присоединяются массы с нулевой абсолютной скоростью, а на заднем фронте – отделяются массы, абсолютные скорости которых направлены по оси 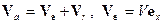 , если подвижная система координат связана с движущимся телом. Относительная скорость направлена по касательной к кривой образующей поверхность тела угол
, если подвижная система координат связана с движущимся телом. Относительная скорость направлена по касательной к кривой образующей поверхность тела угол  (рис.3). В результате получим
(рис.3). В результате получим 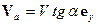 .
.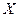
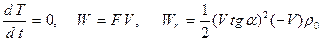
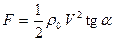 , т.е. сила сопротивления движения, обусловленная переменностью состава системы, пропорциональна квадрату скорости тела.
, т.е. сила сопротивления движения, обусловленная переменностью состава системы, пропорциональна квадрату скорости тела.


