Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Движение однородного шара по шероховатой плоскостиСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Пусть однородный шар радиуса
Здесь
где
из которого определяется угловая скорость шара при заданной силе и моменте сил. Пусть шар катится по наклонной плоскости, когда
Центр масс шара согласно (2) будет двигаться по закону
Описывая в наклонной плоскости параболу. Качение шара без проскальзывания обеспечивается за счет силы сухого трения в точке контакта. Компоненты реакции связи в точке контакта определяются из первого уравнения системы (1) с учетом соотношений (4)
Качение шара без проскальзывания будет возможно, если величина реакции связей не превосходит максимального значения силы трения. Это условие выражается неравенством Рассмотрим движение шара по горизонтальной шероховатой плоскости
Пусть на шар не действуют внешние активные силы и моменты, кроме силы тяжести. Уравнения (1) в этом случае примут вид
Воспользуемся соотношением (2) для скорости точки контакта и найдем
Отметим, что производная единичного вектора ортогональна ему самому. Далее найдем
В уравнения (6) угловое ускорение
Согласно (7) центр масс шара движется по параболе и одновременно уменьшается по линейному закону модуль скорости в точке контакта шара с плоскостью. Изменение угловой скорости шара найдем из второго уравнения системы (5) представленного в виде
После прекращения проскальзывания угловая скорость шара будет оставаться постоянной в силу соотношения (2) и постоянства скорости центра масс шара.
ПОВЕДЕНИЕ СОБСТВЕННЫХ ЧАСТОТ ПРИ НАЛОЖЕНИИ СВЯЗИ (комментарий и добавление к соответствующему параграфу учебника) 1. Рассматривается случай общего положения, когда все собственные частоты различны и все 2. Если 3. Допустим, что система имеет кратные собственные частоты, например,
Введем в пространстве
Отсюда согласно п. 2 следует, что нормальным координатам
ЗАДАЧА КЕПЛЕРА - НЬЮТОНА В ПЕРЕМЕННЫХ ДЕЛОНЕ. ПЕРТУРБАЦИОННАЯ ФУНКЦИЯ. В качестве примера использования канонических переменных действие – угол и метода усреднения рассмотрим задачу Кеплера – Ньютона о движении материальной точки в центральном поле притяжения по закону Всемирного тяготения при наличии консервативных и неконсервативных возмущений. Рассмотрим частный случай, когда возмущающие силы находятся в плоскости, в которой происходит невозмущенное движение. В невозмущенной задаче сохраняется вектор момента количества движения, а движение происходит по эллипсу, расположенному в ортогональной плоскости
Полный интеграл уравнения Гамильтона – Якоби
согласно методу разделения движений найдем в виде
Знак плюс или минус перед интегралом выбирается в зависимости от того положителен или отрицателен импульс
Отсюда следует, что величина Примем в качестве производящей функции канонического преобразования функции
Полученные канонические переменные
Из которых следует, что все канонические переменные, кроме «быстрой» переменной Выясним механический смысл угловых переменных. Первое равенство в (1) представим в форме
С помощью подстановки Переменная
Отсюда следует, что угловая переменная Рассмотрим два вида возмущений, одно из которых порождается дополнительным членом в выражении гамильтониана
Обобщенные силы в уравнениях (3) определяются из выражения элементарной работы
Уравнения (3) получены из вариационного принципа Гамильтона – Остроградского в форме Пуанкаре при наличии неконсервативных сил
Роль канонических переменных в данном случае играют переменные Делоне. Система уравнений (3) имеет стандартный вид для применения метода усреднения, поскольку она состоит из одного уравнения для быстрой переменной
Определение средних значений в некоторых случаях удобно производить с использованием истинной аномалии
ЭВОЛЮЦИЯ ВОЗМУЩЕННОГО ДВИЖЕНИЯ ПЛАНЕТЫ Рассмотрим два вида возмущений, одно из которых порождается дополнительным членом в выражении гамильтониана
Обобщенные силы в уравнениях (1) определяются из выражения элементарной работы
Система уравнений (1) имеет стандартный вид для применения метода усреднения, поскольку она состоит из одного уравнения для быстрой переменной
Согласно определению среднего значения получим следующее выражение
Учитывая равенства
найдем
Уравнение, описывающее эволюцию переменной
Отсюда следует, что каноническая переменная Каноническая переменная
Поскольку функция
Операции интегрирования при вычислении среднего значения и дифференцирования по параметру можно выполнять в любой последовательности, что и было использовано в предыдущем соотношении. Воспользуемся равенством
при вычислении интеграла и получим
Усредненное уравнение для переменной
Перигей орбиты медленно вращается против часовой стрелки, что означает прецессию невозмущенной орбиты в процессе ее эволюции. Отметим, что за это явление отвечает консервативное возмущение исходного гамильтониана, а изменение эксцентриситета орбиты вызывается воздействием диссипативных сил.
|
||||||||
|
Последнее изменение этой страницы: 2016-08-10; просмотров: 715; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.221.240.14 (0.012 с.) |

 катится по плоскости
катится по плоскости 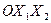 без проскальзывания под действие силы
без проскальзывания под действие силы  , приложенной к центру шара, и момента сил
, приложенной к центру шара, и момента сил  . В точке
. В точке  контакта шара с плоскостью на него действует реакция связи
контакта шара с плоскостью на него действует реакция связи  . Тензор инерции шара относительно центра масс точки
. Тензор инерции шара относительно центра масс точки  представляется шаровым тензором
представляется шаровым тензором  , где
, где  - масса шара. Теоремы о движении центра масс и об изменении момента количеств движения относительно центра масс представляются в форме
- масса шара. Теоремы о движении центра масс и об изменении момента количеств движения относительно центра масс представляются в форме (1)
(1) - радиус-вектор центра масс шара и его угловая скорость,
- радиус-вектор центра масс шара и его угловая скорость,  - орт оси
- орт оси  . Условие качения шара бае проскальзывания в точке контакта имеет вид
. Условие качения шара бае проскальзывания в точке контакта имеет вид (2)
(2) - скорость точки контакта. Исключая реакцию связей из уравнений (1), получим уравнение
- скорость точки контакта. Исключая реакцию связей из уравнений (1), получим уравнение (3)
(3) , где
, где  - угол наклона плоскости к горизонту. В этом случае уравнение (3) примет вид
- угол наклона плоскости к горизонту. В этом случае уравнение (3) примет вид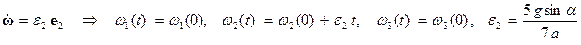
 (4)
(4)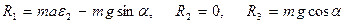
 или
или  . Кроме этого необходимо, чтобы в начальный момент времени выполнялось условие (2) на скорость точки
. Кроме этого необходимо, чтобы в начальный момент времени выполнялось условие (2) на скорость точки 
 (5)
(5)
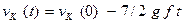 и момент времени
и момент времени  , когда скорость проскальзывания в точке контакта обращается в нуль. Начиная с этого момента шар будет катиться без проскальзывания согласно соотношениям (4), представленным в виде
, когда скорость проскальзывания в точке контакта обращается в нуль. Начиная с этого момента шар будет катиться без проскальзывания согласно соотношениям (4), представленным в виде (6)
(6) , так как плоскость
, так как плоскость  из первого уравнения системы (5) найдем движение центра масс шара и его скорость
из первого уравнения системы (5) найдем движение центра масс шара и его скорость (7)
(7)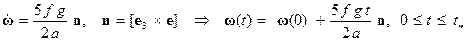
 . В этом случае все рассуждения соответствую учебнику, и результат следующий:
. В этом случае все рассуждения соответствую учебнику, и результат следующий:  .
.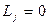 , то уравнение малых колебаний для нормальной координаты с номером
, то уравнение малых колебаний для нормальной координаты с номером  остается неизменным. Следовательно, не изменяется нормальная форма колебаний и собственная частота
остается неизменным. Следовательно, не изменяется нормальная форма колебаний и собственная частота  .
. которым соответствует собственное линейное подпространство
которым соответствует собственное линейное подпространство  размерности
размерности  . Уравнение линейной связи в нормальных координатах имеет вид
. Уравнение линейной связи в нормальных координатах имеет вид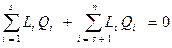
 и обозначив ортогональные ей координаты через
и обозначив ортогональные ей координаты через  . Уравнение линейной связи в новых переменных примет вид
. Уравнение линейной связи в новых переменных примет вид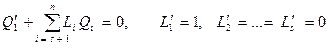
 будут соответствовать одинаковые собственные частоты
будут соответствовать одинаковые собственные частоты  кратности
кратности  , а изменение нормальных форм и собственных частот для оставшихся координат
, а изменение нормальных форм и собственных частот для оставшихся координат  происходит согласно п. 1.
происходит согласно п. 1.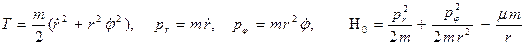


 . Выясним смысл постоянных величин
. Выясним смысл постоянных величин  и
и  в выражении полного интеграла. Постоянная
в выражении полного интеграла. Постоянная  и равна значению циклического интеграла
и равна значению циклического интеграла  , т. е. является модулем момента количества движения точки относительно притягивающего центра
, т. е. является модулем момента количества движения точки относительно притягивающего центра  направленного по неподвижной оси
направленного по неподвижной оси  при движении точки по кеплеровской эллиптической орбите. Найдем величину момента количества движения при движении точки по круговой орбите с данным значением полной энергии. В этом случае справедливы соотношения
при движении точки по кеплеровской эллиптической орбите. Найдем величину момента количества движения при движении точки по круговой орбите с данным значением полной энергии. В этом случае справедливы соотношения
 , т. е. равна модулю момента количества движения точки с заданной энергией при движении по круговой орбите.
, т. е. равна модулю момента количества движения точки с заданной энергией при движении по круговой орбите.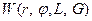 . Заметим, что в новых канонических переменных невозмущенный гамильтониан равен
. Заметим, что в новых канонических переменных невозмущенный гамильтониан равен  . Это означает, что канонические переменные
. Это означает, что канонические переменные  являются переменными действие, а сопряженные им угловые переменные
являются переменными действие, а сопряженные им угловые переменные  определяются по формулам
определяются по формулам (1)
(1) называются переменными Делоне, а канонические уравнения движения в новых переменных имеют вид
называются переменными Делоне, а канонические уравнения движения в новых переменных имеют вид (2)
(2)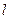 , являются постоянными.
, являются постоянными.
 после интегрирования получим уравнение Кеплера
после интегрирования получим уравнение Кеплера  . Здесь как было обозначено ранее
. Здесь как было обозначено ранее  - большая полуось и эксцентриситет орбиты,
- большая полуось и эксцентриситет орбиты,  - средняя и эксцентрическая аномалии соответственно.
- средняя и эксцентрическая аномалии соответственно. , определенная в (1), постоянна согласно каноническим уравнениям. Далее найдем
, определенная в (1), постоянна согласно каноническим уравнениям. Далее найдем

 - истинная аномалия, связанная с эксцентрической аномалией соотношением
- истинная аномалия, связанная с эксцентрической аномалией соотношением 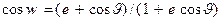 . Заметим, что согласно полученным формулам, радиус
. Заметим, что согласно полученным формулам, радиус  является функцией переменных
является функцией переменных  .
. , а второе задается неконсервативной силой
, а второе задается неконсервативной силой  , определяющей диссипацию энергии. Здесь
, определяющей диссипацию энергии. Здесь  малый параметр в том смысле, что соответствующие возмущающие силы малы по сравнению с основной силой гравитационного взаимодействия точки с притягивающим центром. Функция
малый параметр в том смысле, что соответствующие возмущающие силы малы по сравнению с основной силой гравитационного взаимодействия точки с притягивающим центром. Функция  (3)
(3)

 . Понятие медленной переменной означает, что скорость ее изменения пропорциональна величине малого параметра, т.е. мала по сравнению со скоростью изменения быстрой переменной, имеющей порядок единицы. Скорость изменения быстрой переменной претерпевает малые возмущения. Метод усреднения в данном случае означает замену правых частей уравнений (3) их средними значениями, имея в виду разложения периодических функций, стоящих в правых частях, в ряд Фурье по быстрой переменной
. Понятие медленной переменной означает, что скорость ее изменения пропорциональна величине малого параметра, т.е. мала по сравнению со скоростью изменения быстрой переменной, имеющей порядок единицы. Скорость изменения быстрой переменной претерпевает малые возмущения. Метод усреднения в данном случае означает замену правых частей уравнений (3) их средними значениями, имея в виду разложения периодических функций, стоящих в правых частях, в ряд Фурье по быстрой переменной 

 , а второе определяется диссипативной силой
, а второе определяется диссипативной силой  . Здесь
. Здесь  малые величины в том смысле, что соответствующие возмущающие силы малы по сравнению с основной силой гравитационного взаимодействия точки с притягивающим центром. Заметим, что возмущающие силы являются центральными силами, что влечет сохранения момента количества движения и сохраняет движение плоским. Подобного рода возмущения возникают при рассмотрении вязкоупругих свойств шарообразной деформируемой планеты, заменяющей материальную точку. Канонические уравнения возмущенного движения в переменных Делоне имеют вид
малые величины в том смысле, что соответствующие возмущающие силы малы по сравнению с основной силой гравитационного взаимодействия точки с притягивающим центром. Заметим, что возмущающие силы являются центральными силами, что влечет сохранения момента количества движения и сохраняет движение плоским. Подобного рода возмущения возникают при рассмотрении вязкоупругих свойств шарообразной деформируемой планеты, заменяющей материальную точку. Канонические уравнения возмущенного движения в переменных Делоне имеют вид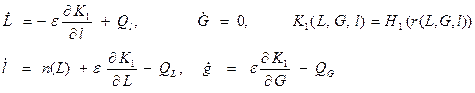 (1)
(1)
 . Переменная
. Переменная 

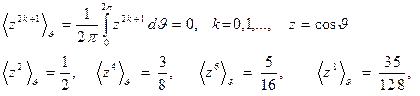


 , а эксцентриситет орбиты
, а эксцентриситет орбиты  стремится к нулю. В результате эволюции эллиптическая орбита стремится к круговой орбите.
стремится к нулю. В результате эволюции эллиптическая орбита стремится к круговой орбите.
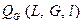 является периодической нечетной функцией относительно переменной
является периодической нечетной функцией относительно переменной