По дополнительным разделам курса «Теоретическая механика»
В.Г.ВИЛЬКЕ
МЕТОДИЧЕСКИЕ МАТЕРИАЛЫ
По дополнительным разделам курса «Теоретическая механика»
для студентов механиков 3, 4 и 5 семестры
ОГРАНИЧЕННАЯ КРУГОВАЯ ЗАДАЧА ТРЕХ ТЕЛ
Пусть два массивных твердых тела (материальные точки  и и  ) с массами ) с массами  и и  вращаются по круговым орбитам вокруг их центра масс с постоянной угловой скоростью под действием силы взаимного притяжения по закону Всемирного тяготения. Пусть тела расположены на оси вращаются по круговым орбитам вокруг их центра масс с постоянной угловой скоростью под действием силы взаимного притяжения по закону Всемирного тяготения. Пусть тела расположены на оси 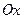 системы координат системы координат  равномерно вращающейся вокруг оси равномерно вращающейся вокруг оси  с единичной угловой скоростью и их координаты равны с единичной угловой скоростью и их координаты равны 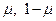 соответственно. соответственно.

Для точки  , описывающей окружность с центром в начале координат, справедливы второй закон Ньютона в проекции на ось , описывающей окружность с центром в начале координат, справедливы второй закон Ньютона в проекции на ось 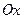 , а именно , а именно  , где , где  - гравитационная постоянная в законе Всемирного тяготения, а - гравитационная постоянная в законе Всемирного тяготения, а  - угловая скорость вращения точки - угловая скорость вращения точки  по круговой орбите. Поскольку эта угловая скорость принята за единицу, то гравитационная постоянная по круговой орбите. Поскольку эта угловая скорость принята за единицу, то гравитационная постоянная  также оказывается равной единице. Напомним, что расстояние между точками также оказывается равной единице. Напомним, что расстояние между точками  и и  принято равным единице. принято равным единице.
Рассмотрим движение материальной точки  с массой с массой   в плоскости в плоскости  под действием притяжения материальных точек под действием притяжения материальных точек  и и  . Будем считать, что обратное влияние точки . Будем считать, что обратное влияние точки  на движение точек на движение точек  и и  пренебрежимо мало, что возможно, если пренебрежимо мало, что возможно, если  . Эта задача носит название ограниченной круговой задачи трех тел. Уравнение движение в неинерциальной системе координат . Эта задача носит название ограниченной круговой задачи трех тел. Уравнение движение в неинерциальной системе координат  запишем в виде запишем в виде
 (1) (1)
Здесь  - орт оси - орт оси  , , 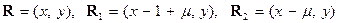 - векторы - векторы  соответственно, а соответственно, а 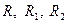 - их модули. Два последних члена в уравнении (1) представляют центробежную силу инерции и силу инерции Кориолиса. Система двух уравнений (1) относительно переменных - их модули. Два последних члена в уравнении (1) представляют центробежную силу инерции и силу инерции Кориолиса. Система двух уравнений (1) относительно переменных  не интегрируется в общем случае, хотя и имеет один первый интеграл, представляющий закон сохранения обобщенной энергии (интеграл Якоби) не интегрируется в общем случае, хотя и имеет один первый интеграл, представляющий закон сохранения обобщенной энергии (интеграл Якоби)

Относительные равновесия точки  в системе координат в системе координат  являются стационарными точками эффективной потенциальной энергии являются стационарными точками эффективной потенциальной энергии  и удовлетворяют соотношениям и удовлетворяют соотношениям
 (2) (2)
Второе уравнение системы (2) допускает решение  . В этом случае эффективная потенциальная энергия становится функцией одного аргумента . В этом случае эффективная потенциальная энергия становится функцией одного аргумента  и принимает вид и принимает вид

Функция  принимает отрицательные значения, при принимает отрицательные значения, при  стремящемся к плюс или минус бесконечности стремится к минус бесконечности. Она имеет две вертикальные асимптоты при стремящемся к плюс или минус бесконечности стремится к минус бесконечности. Она имеет две вертикальные асимптоты при  и и 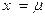 , при приближении к которым с двух сторон функция стремится к минус бесконечности. У функция , при приближении к которым с двух сторон функция стремится к минус бесконечности. У функция  есть три локальных максимума в точках есть три локальных максимума в точках  , удовлетворяющих неравенствам , удовлетворяющих неравенствам  . Эти положения равновесия называются точками либрации Эйлера и обозначаются буквами . Эти положения равновесия называются точками либрации Эйлера и обозначаются буквами 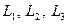 . .
Кроме рассмотренного выше решения, второе уравнение системы (2) допускает решение, удовлетворяющее соотношению
 (3) (3)
В этом случае из первого уравнения системы (2) следует равенство
 (4) (4)
Тогда из уравнений (3), (4) получим  . Последнее означает, что точки . Последнее означает, что точки  образуют равносторонний треугольник со стороной единица. Можно построить два таких треугольника, когда ордината вершины образуют равносторонний треугольник со стороной единица. Можно построить два таких треугольника, когда ордината вершины  положительна или отрицательна. Эти точки обозначаются буквами положительна или отрицательна. Эти точки обозначаются буквами 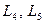 и называются точками либрации Лагранжа. и называются точками либрации Лагранжа.
ВТОРОЙ МЕТОД ЛЯПУНОВА ИССЛЕДОВАНИЯ УСТОЙЧИВОСТИ.
МЕТОД РАУСА ИГНОРИРОВАНИЯ ЦИКЛИЧЕСКИХ КООРДИНАТ.
УРАВНЕНИЯ РАУСА.
Допустим, что обобщенные координаты разбиваются на две группы: циклические координаты  , от которых не зависит функция Лагранжа, и позиционные координаты , от которых не зависит функция Лагранжа, и позиционные координаты  , входящие явно в функцию Лагранжа, которая в этом случае имеет вид , входящие явно в функцию Лагранжа, которая в этом случае имеет вид
 (1) (1)
Уравнения Лагранжа второго рода
 (2) (2)
имеют циклические первые интегралы
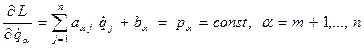 (3) (3)
Здесь 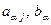 - компоненты матрицы - компоненты матрицы  и вектора и вектора  соответственно. Соотношения (3) представляют систему линейных алгебраических уравнений относительно неизвестных соответственно. Соотношения (3) представляют систему линейных алгебраических уравнений относительно неизвестных  , определитель которой является одним из диагональных миноров матрицы , определитель которой является одним из диагональных миноров матрицы  , порождающей положительно определенную квадратичную форму в выражении функции Лагранжа. Положительная определенность этой формы следует из определения кинетической энергии системы. Согласно критерию Сильвестра этот определитель положителен и рассматриваемая система уравнений имеет решение , порождающей положительно определенную квадратичную форму в выражении функции Лагранжа. Положительная определенность этой формы следует из определения кинетической энергии системы. Согласно критерию Сильвестра этот определитель положителен и рассматриваемая система уравнений имеет решение
 (4) (4)
где  - компоненты обратной матрицы диагонального минора - компоненты обратной матрицы диагонального минора 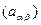 . .
Следуя идее Рауса, получим систему дифференциальных уравнений порядка 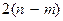 , описывающих изменение только позиционных координат. Определим функцию Рауса в виде , описывающих изменение только позиционных координат. Определим функцию Рауса в виде
 (5) (5)
Полный дифференциал функции Рауса представим двумя выражениями

Приравнивая коэффициенты при одинаковых дифференциалах, получим равенства
 (6) (6)
Заменим в  первых уравнениях системы (2) частные производные функции Лагранжа согласно равенствам (6) на частные производные функции Рауса и получим систему уравнений Рауса первых уравнениях системы (2) частные производные функции Лагранжа согласно равенствам (6) на частные производные функции Рауса и получим систему уравнений Рауса
 (7) (7)
Заметим, что значения циклических интегралов в функции Рауса определяются начальными условиями движения и в дальнейшем не меняются. После того как найдено решение уравнений Рауса, т.е. зависимости  , циклические координаты находятся путем вычисления интегралов по времени , циклические координаты находятся путем вычисления интегралов по времени
 (8) (8)
Как и в случае уравнений Лагранжа, из уравнений Рауса получается интеграл обобщенной энергии, если функции Лагранжа и Рауса не зависят явно от времени

Уравнения Рауса полностью аналогичны уравнениям Лагранжа и имеют те же свойства, только порядок этих уравнений на 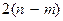 единиц меньше, чем у соответствующих уравнений Лагранжа, и имеет место зависимость функции Рауса от единиц меньше, чем у соответствующих уравнений Лагранжа, и имеет место зависимость функции Рауса от  параметров – постоянных циклических интегралов. параметров – постоянных циклических интегралов.
СФЕРИЧЕСКИЙ МАЯТНИК
Пусть в механической системе имеется  циклических координат, и соответствующая функция Рауса не зависит явно от времени. циклических координат, и соответствующая функция Рауса не зависит явно от времени.
О. Решение уравнений Рауса, соответствующее постоянным значениям позиционных координат  , при заданных значениях циклических интегралов, называется стационарным движением исходной системы уравнений Лагранжа. , при заданных значениях циклических интегралов, называется стационарным движением исходной системы уравнений Лагранжа.
Циклические координаты при этом являются линейными функциями времени, поскольку согласно соотношениям (8) подынтегральная функция постоянна на стационарном движении, и, следовательно,
 (9) (9)
Устойчивость стационарных движений исследуется как устойчивость положений равновесия по позиционным координатам на основании уравнений Рауса. В этом случае возможно применение теоремы Лагранжа об устойчивости положения равновесия в ее модифицированном виде или второго метода Ляпунова. Значения постоянных циклических интегралов можно возмущать или считать их неизменными на возмущенных движениях.
В качестве примера рассмотрим задачу о сферическом маятнике, функция Лагранжа которого имеет вид

Здесь  - масса материально точки, длина маятника и ускорение свободного падения, - масса материально точки, длина маятника и ускорение свободного падения, 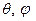 - сферические координаты. Угол - сферические координаты. Угол  отсчитывается от нижнего положения равновесия, когда маятник висит по вертикали, а угол отсчитывается от нижнего положения равновесия, когда маятник висит по вертикали, а угол  составляет вертикальная плоскость, в которой находится маятник и его точка подвеса, с аналогичной плоскостью в начальный момент движения. Угол составляет вертикальная плоскость, в которой находится маятник и его точка подвеса, с аналогичной плоскостью в начальный момент движения. Угол  , а угол , а угол  задан по модулю задан по модулю  . Ясно, что координата . Ясно, что координата  циклическая, и справедливы следующие соотношения циклическая, и справедливы следующие соотношения

Уравнение Рауса примет вид

Стационарное движение маятника соответствует экстремуму измененной потенциальной энергии

Угол  в положении равновесия является корнем последнего уравнения (стационарная точка измененной потенциальной энергии) в положении равновесия является корнем последнего уравнения (стационарная точка измененной потенциальной энергии)  . Для определения устойчивости стационарного движения воспользуемся теоремой Лагранжа, для чего вычислим вторую производную в стационарной точке . Для определения устойчивости стационарного движения воспользуемся теоремой Лагранжа, для чего вычислим вторую производную в стационарной точке
 (10) (10)
Из неравенства (10) следует, что стационарная точка является изолированным минимумом измененной потенциальной энергии, и, значит, стационарное движение устойчиво по Ляпунову.
Циклическая координата изменяется по закону

ПЕРТУРБАЦИОННАЯ ФУНКЦИЯ.
В качестве примера использования канонических переменных действие – угол и метода усреднения рассмотрим задачу Кеплера – Ньютона о движении материальной точки в центральном поле притяжения по закону Всемирного тяготения при наличии консервативных и неконсервативных возмущений. Рассмотрим частный случай, когда возмущающие силы находятся в плоскости, в которой происходит невозмущенное движение. В невозмущенной задаче сохраняется вектор момента количества движения, а движение происходит по эллипсу, расположенному в ортогональной плоскости 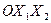 . В полярной системе координат кинетическая энергия, обобщенные импульсы и функция Гамильтона записываются в виде . В полярной системе координат кинетическая энергия, обобщенные импульсы и функция Гамильтона записываются в виде
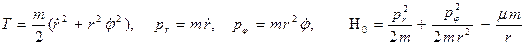
Полный интеграл уравнения Гамильтона – Якоби

согласно методу разделения движений найдем в виде

Знак плюс или минус перед интегралом выбирается в зависимости от того положителен или отрицателен импульс  . Выясним смысл постоянных величин . Выясним смысл постоянных величин  и и  в выражении полного интеграла. Постоянная в выражении полного интеграла. Постоянная  соответствует циклической переменной соответствует циклической переменной  и равна значению циклического интеграла и равна значению циклического интеграла  , т. е. является модулем момента количества движения точки относительно притягивающего центра , т. е. является модулем момента количества движения точки относительно притягивающего центра  направленного по неподвижной оси направленного по неподвижной оси  . Постоянная . Постоянная  связана со значением интеграла полной механической энергии связана со значением интеграла полной механической энергии  при движении точки по кеплеровской эллиптической орбите. Найдем величину момента количества движения при движении точки по круговой орбите с данным значением полной энергии. В этом случае справедливы соотношения при движении точки по кеплеровской эллиптической орбите. Найдем величину момента количества движения при движении точки по круговой орбите с данным значением полной энергии. В этом случае справедливы соотношения

Отсюда следует, что величина  , т. е. равна модулю момента количества движения точки с заданной энергией при движении по круговой орбите. , т. е. равна модулю момента количества движения точки с заданной энергией при движении по круговой орбите.
Примем в качестве производящей функции канонического преобразования функции 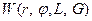 . Заметим, что в новых канонических переменных невозмущенный гамильтониан равен . Заметим, что в новых канонических переменных невозмущенный гамильтониан равен  . Это означает, что канонические переменные . Это означает, что канонические переменные  являются переменными действие, а сопряженные им угловые переменные являются переменными действие, а сопряженные им угловые переменные  определяются по формулам определяются по формулам
 (1) (1)
Полученные канонические переменные  называются переменными Делоне, а канонические уравнения движения в новых переменных имеют вид называются переменными Делоне, а канонические уравнения движения в новых переменных имеют вид
 (2) (2)
Из которых следует, что все канонические переменные, кроме «быстрой» переменной 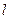 , являются постоянными. , являются постоянными.
Выясним механический смысл угловых переменных. Первое равенство в (1) представим в форме

С помощью подстановки  после интегрирования получим уравнение Кеплера после интегрирования получим уравнение Кеплера  . Здесь как было обозначено ранее . Здесь как было обозначено ранее  - большая полуось и эксцентриситет орбиты, - большая полуось и эксцентриситет орбиты,  - средняя и эксцентрическая аномалии соответственно. - средняя и эксцентрическая аномалии соответственно.
Переменная  , определенная в (1), постоянна согласно каноническим уравнениям. Далее найдем , определенная в (1), постоянна согласно каноническим уравнениям. Далее найдем


Отсюда следует, что угловая переменная  определяет полярный угол перигея эллиптической орбиты, а угол определяет полярный угол перигея эллиптической орбиты, а угол  - истинная аномалия, связанная с эксцентрической аномалией соотношением - истинная аномалия, связанная с эксцентрической аномалией соотношением 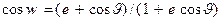 . Заметим, что согласно полученным формулам, радиус . Заметим, что согласно полученным формулам, радиус  является функцией переменных является функцией переменных  . .
Рассмотрим два вида возмущений, одно из которых порождается дополнительным членом в выражении гамильтониана  , а второе задается неконсервативной силой , а второе задается неконсервативной силой  , определяющей диссипацию энергии. Здесь , определяющей диссипацию энергии. Здесь  малый параметр в том смысле, что соответствующие возмущающие силы малы по сравнению с основной силой гравитационного взаимодействия точки с притягивающим центром. Функция малый параметр в том смысле, что соответствующие возмущающие силы малы по сравнению с основной силой гравитационного взаимодействия точки с притягивающим центром. Функция  называется пертурбационной. Канонические уравнения возмущенного движения в переменных Делоне имеют вид называется пертурбационной. Канонические уравнения возмущенного движения в переменных Делоне имеют вид
 (3) (3)
Обобщенные силы в уравнениях (3) определяются из выражения элементарной работы

Уравнения (3) получены из вариационного принципа Гамильтона – Остроградского в форме Пуанкаре при наличии неконсервативных сил

Роль канонических переменных в данном случае играют переменные Делоне. Система уравнений (3) имеет стандартный вид для применения метода усреднения, поскольку она состоит из одного уравнения для быстрой переменной 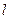 и трех уравнений для медленных переменных и трех уравнений для медленных переменных  . Понятие медленной переменной означает, что скорость ее изменения пропорциональна величине малого параметра, т.е. мала по сравнению со скоростью изменения быстрой переменной, имеющей порядок единицы. Скорость изменения быстрой переменной претерпевает малые возмущения. Метод усреднения в данном случае означает замену правых частей уравнений (3) их средними значениями, имея в виду разложения периодических функций, стоящих в правых частях, в ряд Фурье по быстрой переменной . Понятие медленной переменной означает, что скорость ее изменения пропорциональна величине малого параметра, т.е. мала по сравнению со скоростью изменения быстрой переменной, имеющей порядок единицы. Скорость изменения быстрой переменной претерпевает малые возмущения. Метод усреднения в данном случае означает замену правых частей уравнений (3) их средними значениями, имея в виду разложения периодических функций, стоящих в правых частях, в ряд Фурье по быстрой переменной 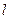 . Таким образом, функции, стоящие в правых частях уравнений (3) следует заменить их средними значениями . Таким образом, функции, стоящие в правых частях уравнений (3) следует заменить их средними значениями

Определение средних значений в некоторых случаях удобно производить с использованием истинной аномалии  , так как от нее зависят подынтегральные функции. Согласно ранее приведенным формулам найдем , так как от нее зависят подынтегральные функции. Согласно ранее приведенным формулам найдем

ЭВОЛЮЦИЯ ВОЗМУЩЕННОГО ДВИЖЕНИЯ ПЛАНЕТЫ
Рассмотрим два вида возмущений, одно из которых порождается дополнительным членом в выражении гамильтониана  , а второе определяется диссипативной силой , а второе определяется диссипативной силой  . Здесь . Здесь  и и  малые величины в том смысле, что соответствующие возмущающие силы малы по сравнению с основной силой гравитационного взаимодействия точки с притягивающим центром. Заметим, что возмущающие силы являются центральными силами, что влечет сохранения момента количества движения и сохраняет движение плоским. Подобного рода возмущения возникают при рассмотрении вязкоупругих свойств шарообразной деформируемой планеты, заменяющей материальную точку. Канонические уравнения возмущенного движения в переменных Делоне имеют вид малые величины в том смысле, что соответствующие возмущающие силы малы по сравнению с основной силой гравитационного взаимодействия точки с притягивающим центром. Заметим, что возмущающие силы являются центральными силами, что влечет сохранения момента количества движения и сохраняет движение плоским. Подобного рода возмущения возникают при рассмотрении вязкоупругих свойств шарообразной деформируемой планеты, заменяющей материальную точку. Канонические уравнения возмущенного движения в переменных Делоне имеют вид
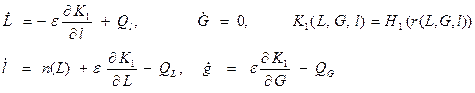 (1) (1)
Обобщенные силы в уравнениях (1) определяются из выражения элементарной работы

Система уравнений (1) имеет стандартный вид для применения метода усреднения, поскольку она состоит из одного уравнения для быстрой переменной 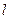 и двух уравнений для медленных переменных и двух уравнений для медленных переменных  . Переменная . Переменная  в рассматриваемом случае остается постоянной при наличии возмущений. Понятие медленной переменной означает, что скорость ее изменения пропорциональна величине малого параметра, т.е. мала по сравнению со скоростью изменения быстрой переменной, имеющей порядок единицы. Скорость изменения быстрой переменной претерпевает малые возмущения. Усредним правые части уравнений (1) по быстрой переменной в рассматриваемом случае остается постоянной при наличии возмущений. Понятие медленной переменной означает, что скорость ее изменения пропорциональна величине малого параметра, т.е. мала по сравнению со скоростью изменения быстрой переменной, имеющей порядок единицы. Скорость изменения быстрой переменной претерпевает малые возмущения. Усредним правые части уравнений (1) по быстрой переменной 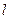 и получим эволюционные уравнения для медленных переменных и получим эволюционные уравнения для медленных переменных  и и  , сохранив для усредненных значений переменных исходные обозначения. Имеем , сохранив для усредненных значений переменных исходные обозначения. Имеем

Согласно определению среднего значения получим следующее выражение

Учитывая равенства
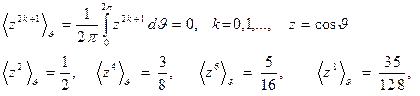
найдем

Уравнение, описывающее эволюцию переменной  , представляется в виде , представляется в виде

Отсюда следует, что каноническая переменная  убывает и стремится к стационарному значению убывает и стремится к стационарному значению  , а эксцентриситет орбиты , а эксцентриситет орбиты  стремится к нулю. В результате эволюции эллиптическая орбита стремится к круговой орбите. стремится к нулю. В результате эволюции эллиптическая орбита стремится к круговой орбите.
Каноническая переменная  , определяющая полярный угол перигея орбиты, изменяется согласно усредненному уравнению системы (1) , определяющая полярный угол перигея орбиты, изменяется согласно усредненному уравнению системы (1)

Поскольку функция 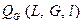 является периодической нечетной функцией относительно переменной является периодической нечетной функцией относительно переменной 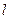 , то ее среднее значение по этой переменной равно нулю. Далее получим , то ее среднее значение по этой переменной равно нулю. Далее получим

Операции интегрирования при вычислении среднего значения и дифференцирования по параметру можно выполнять в любой последовательности, что и было использовано в предыдущем соотношении. Воспользуемся равенством

при вычислении интеграла и получим
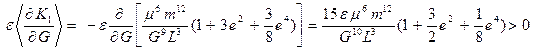
Усредненное уравнение для переменной  представляется в форме представляется в форме

Перигей орбиты медленно вращается против часовой стрелки, что означает прецессию невозмущенной орбиты в процессе ее эволюции. Отметим, что за это явление отвечает консервативное возмущение исходного гамильтониана, а изменение эксцентриситета орбиты вызывается воздействием диссипативных сил.
ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА ВОКРУГ НЕПОДВИЖНОЙ ТОЧКИ С НЕГОЛОНОМНОЙ СВЯЗЬЮ (ЗАДАЧА Г.К.СУСЛОВА)
Пусть система координат  неподвижна, а система координат неподвижна, а система координат  связана с твердым телом. На теле в точке связана с твердым телом. На теле в точке  на оси, лежащей в плоскости на оси, лежащей в плоскости  , закреплен конек, лезвие которого направлено вдоль оси , закреплен конек, лезвие которого направлено вдоль оси  и который скользит по неподвижной сфере с центром в точке и который скользит по неподвижной сфере с центром в точке  (рис.1). Пусть вектор (рис.1). Пусть вектор  , где , где  – орт оси – орт оси  . Скорость точки . Скорость точки  направлена вдоль оси направлена вдоль оси  , поскольку скольжение конька происходит вдоль его лезвия. В результате оказывается справедливым равенство , поскольку скольжение конька происходит вдоль его лезвия. В результате оказывается справедливым равенство
 (1) (1)
Здесь  – угловая скорость твердого тела. Тело вращается вокруг неподвижной точки по инерции. На движение тела наложена неголономная связь (1). В точке контакта конька с неподвижной сферой на тело действует реакция неголономной связи – сила, направленная по оси с направляющим вектором – угловая скорость твердого тела. Тело вращается вокруг неподвижной точки по инерции. На движение тела наложена неголономная связь (1). В точке контакта конька с неподвижной сферой на тело действует реакция неголономной связи – сила, направленная по оси с направляющим вектором 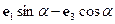 . Момент этой силы относительно неподвижной точки . Момент этой силы относительно неподвижной точки  равен равен  . .

Рис. 1
Динамические уравнения Эйлера движения твердого тела с неподвижной точкой имеют вид
 (2) (2)
Здесь  – тензор инерции тела относительно системы координат – тензор инерции тела относительно системы координат  . Равенство нулю центробежного момента инерции . Равенство нулю центробежного момента инерции  достигается соответствующим выбором угла достигается соответствующим выбором угла  . Умножим уравнение (2) скалярно на вектор угловой скорости . Умножим уравнение (2) скалярно на вектор угловой скорости  и получим первый интеграл – закон сохранения кинетической энергии и получим первый интеграл – закон сохранения кинетической энергии
 (3) (3)
В явном виде соотношение (3) с учетом равенства нулю проекции угловой скорости тела  примет вид примет вид
 (4) (4)
Уравнение (4) является уравнением эллипса на плоскости  . Уравнения движения (2) в проекциях на оси . Уравнения движения (2) в проекциях на оси  и и  имеют вид имеют вид
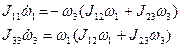 (5) (5)
Стационарные решения уравнений (5), когда их правые части обращаются в нуль, соответствуют перманентным вращениям вокруг оси, лежащей в плоскости  . Правые части уравнений (5) обращаются в нуль, когда в начальный момент времени выполняется равенство . Правые части уравнений (5) обращаются в нуль, когда в начальный момент времени выполняется равенство
 (6) (6)
В дальнейшем угловая скорость не меняется в силу уравнений (5). Существует вырожденный случай, когда центробежные моменты инерции  . В этом случае любая ось, проходящая через начало координат и лежащая в плоскости . В этом случае любая ось, проходящая через начало координат и лежащая в плоскости  , может служить осью перманентного вращения при надлежащем выборе начальных условий. , может служить осью перманентного вращения при надлежащем выборе начальных условий.
Исследуем устойчивость стационарных точек уравнений (5), используя уравнения в вариациях. Пусть  . Уравнения в вариациях имеют вид . Уравнения в вариациях имеют вид
 (7) (7)
Характеристическое уравнение линейной системы дифференциальных уравнений с постоянными коэффициентами представляется в форме
 (8) (8)
Характеристическое уравнение (8) имеет один нулевой корень, который возникает как следствие существования интеграла энергии. Второй действительный корень является линейной комбинацией начальных значений проекций угловых скоростей 
 (9) (9)
Первому интегралу (4) удовлетворяют две пары начальных условий  , которым соответствуют перманентные вращения вокруг одной и той же оси, но в разных направлениях. В зависимости от знака соответствующего корня (9) одно из этих вращений оказывается устойчивым, а второе – неустойчивым. Общая картина движения на плоскости переменных , которым соответствуют перманентные вращения вокруг одной и той же оси, но в разных направлениях. В зависимости от знака соответствующего корня (9) одно из этих вращений оказывается устойчивым, а второе – неустойчивым. Общая картина движения на плоскости переменных  представлена на рисунке 2. представлена на рисунке 2.

Рис. 2
 – неустойчивое стационарное вращение, – неустойчивое стационарное вращение,  – устойчивое стационарное вращение. – устойчивое стационарное вращение.
Эллипс является множеством точек, на котором выполняется условие (4). Если начальные условия движения выбрать на эллипсе вблизи точки  , то вращение тела происходит таким образом, что изображающая точка движется по эллипсу. Как видно из рисунка, возможны два сценария движения по эллипсу в зависимости от возмущений начальных условий: движение по стрелке часов или движение в противоположном направлении. Отметим, что в начале движения ось вращения тела достаточно долго остается в окрестности неустойчивого стационарного вращения, а затем быстро переходит в окрестность устойчивого стационарного вращения, и затем асимптотически стремиться к нему. , то вращение тела происходит таким образом, что изображающая точка движется по эллипсу. Как видно из рисунка, возможны два сценария движения по эллипсу в зависимости от возмущений начальных условий: движение по стрелке часов или движение в противоположном направлении. Отметим, что в начале движения ось вращения тела достаточно долго остается в окрестности неустойчивого стационарного вращения, а затем быстро переходит в окрестность устойчивого стационарного вращения, и затем асимптотически стремиться к нему.
Найдем решение уравнений (5). Сделаем замену переменных
 (10) (10)
при которой интеграл энергии (4) превращается в тождество при любом  . Первое уравнение системы (5) примет вид . Первое уравнение системы (5) примет вид
 (11) (11)
Уравнение (11) с разделяющимися переменными представим в форме

и далее найдем
 (12) (12)
где 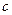 – произвольная постоянная. Правая часть уравнения (12) стремится к бесконечности, когда – произвольная постоянная. Правая часть уравнения (12) стремится к бесконечности, когда  стремится к бесконечности. Следовательно, стремится к бесконечности. Следовательно,  или или  , когда время стремится к бесконечности. Знаки плюс или минус соответствуют двум возможным сценариям движения, отмеченным выше, когда движение тела стремится к стационарному вращению вокруг прямой , когда время стремится к бесконечности. Знаки плюс или минус соответствуют двум возможным сценариям движения, отмеченным выше, когда движение тела стремится к стационарному вращению вокруг прямой  . В стационарном движении конек описывает окружность на сфере радиуса . В стационарном движении конек описывает окружность на сфере радиуса 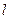 . Центр окружности лежит на оси вращения твердого тела. . Центр окружности лежит на оси вращения твердого тела.
Отметим, что углы Эйлера, определяющие ориентацию твердого тела, удовлетворяют системе уравнений, полученной из кинематических уравнений Эйлера

в которой функции времени  определяются из соотношений (10), (12). определяются из соотношений (10), (12).
Литература: Суслов Г.К. Теоретическая механика. ОГИЗ. М.-Л. 1946. 655 с.
ОСНОВНЫЕ ПОНЯТИЯ И ТЕОРЕМЫ
Рассмотрим механическую систему постоянного состава  и однопараметрическое семейство замкнутых областей и однопараметрическое семейство замкнутых областей  , , 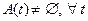 . Пусть . Пусть  – масса материальных точек, образующих множество – масса материальных точек, образующих множество  . Рассмотрим движение механической системы . Рассмотрим движение механической системы  . .
Пусть  – поле скоростей точек границы множества – поле скоростей точек границы множества  , направленное по единичной внешней нормали , направленное по единичной внешней нормали  к поверхности границы к поверхности границы  . Тогда . Тогда
 (1) (1)
Здесь  – поверхностная мера, индуцированная пространственной мерой – поверхностная мера, индуцированная пространственной мерой  . Например, в случае существования плотности . Например, в случае существования плотности  справедливы равенства справедливы равенства  , где , где  – элемент площади поверхности – элемент площади поверхности  . .
О. Механической системой переменного состава называется система  , если , если

Уравнение движения системы свободных материальных точек  представляются в виде представляются в виде
 (2) (2)
где  – поле активных массовых сил. Уравнение (2) понимается в смысле равенства двух обобщенных функций, принадлежащих сопряженному пространству к пространству функций, непрерывных по времени и суммируемых по мере – поле активных массовых сил. Уравнение (2) понимается в смысле равенства двух обобщенных функций, принадлежащих сопряженному пространству к пространству функций, непрерывных по времени и суммируемых по мере  на множестве на множестве  . .
Определим количество движения системы переменного состава как вектор
 (3) (3)
Т.1. Производная по времени от количества движения системы переменного состава (3) равна сумме равнодействующей внешних сил  , приложенных к точкам множества , приложенных к точкам множества  , и реактивной силы , и реактивной силы  , порождаемой изменением множества , порождаемой изменением множества 
 (4) (4)
где  – часть границы – часть границы  , в точках которой , в точках которой  , а , а  – часть границы – часть границы  , в точках которой , в точках которой  , ,  – объемная плотность и элемент площади границы – объемная плотность и элемент площади границы  , ,  . .
Рассмотрим моменты времени  , , 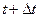 и приращение количества движения системы переменного состава (3) и приращение количества движения системы переменного состава (3)



Рис.1
Функции  как функции времени предполагаются гладкими на множестве как функции времени предполагаются гладкими на множестве  за исключением множеств нулевой меры за исключением множеств нулевой меры  и и  , в которых функция , в которых функция  может иметь разрыва первого рода. Далее с точностью до малых порядка может иметь разрыва первого рода. Далее с точностью до малых порядка  представим полученное приращение в виде представим полученное приращение в виде
 (5) (5)
Здесь  – часть границы – часть границы  | 


 и
и  ) с массами
) с массами  и
и  вращаются по круговым орбитам вокруг их центра масс с постоянной угловой скоростью под действием силы взаимного притяжения по закону Всемирного тяготения. Пусть тела расположены на оси
вращаются по круговым орбитам вокруг их центра масс с постоянной угловой скоростью под действием силы взаимного притяжения по закону Всемирного тяготения. Пусть тела расположены на оси 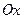 системы координат
системы координат  равномерно вращающейся вокруг оси
равномерно вращающейся вокруг оси  с единичной угловой скоростью и их координаты равны
с единичной угловой скоростью и их координаты равны 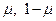 соответственно.
соответственно.
 , где
, где  - гравитационная постоянная в законе Всемирного тяготения, а
- гравитационная постоянная в законе Всемирного тяготения, а  - угловая скорость вращения точки
- угловая скорость вращения точки  с массой
с массой 
 в плоскости
в плоскости  под действием притяжения материальных точек
под действием притяжения материальных точек  . Эта задача носит название ограниченной круговой задачи трех тел. Уравнение движение в неинерциальной системе координат
. Эта задача носит название ограниченной круговой задачи трех тел. Уравнение движение в неинерциальной системе координат  (1)
(1) - орт оси
- орт оси 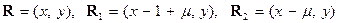 - векторы
- векторы  соответственно, а
соответственно, а 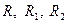 - их модули. Два последних члена в уравнении (1) представляют центробежную силу инерции и силу инерции Кориолиса. Система двух уравнений (1) относительно переменных
- их модули. Два последних члена в уравнении (1) представляют центробежную силу инерции и силу инерции Кориолиса. Система двух уравнений (1) относительно переменных  не интегрируется в общем случае, хотя и имеет один первый интеграл, представляющий закон сохранения обобщенной энергии (интеграл Якоби)
не интегрируется в общем случае, хотя и имеет один первый интеграл, представляющий закон сохранения обобщенной энергии (интеграл Якоби)
 и удовлетворяют соотношениям
и удовлетворяют соотношениям (2)
(2) . В этом случае эффективная потенциальная энергия становится функцией одного аргумента
. В этом случае эффективная потенциальная энергия становится функцией одного аргумента  и принимает вид
и принимает вид
 принимает отрицательные значения, при
принимает отрицательные значения, при  и
и 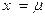 , при приближении к которым с двух сторон функция стремится к минус бесконечности. У функция
, при приближении к которым с двух сторон функция стремится к минус бесконечности. У функция  , удовлетворяющих неравенствам
, удовлетворяющих неравенствам  . Эти положения равновесия называются точками либрации Эйлера и обозначаются буквами
. Эти положения равновесия называются точками либрации Эйлера и обозначаются буквами 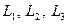 .
. (3)
(3) (4)
(4) . Последнее означает, что точки
. Последнее означает, что точки  образуют равносторонний треугольник со стороной единица. Можно построить два таких треугольника, когда ордината вершины
образуют равносторонний треугольник со стороной единица. Можно построить два таких треугольника, когда ордината вершины 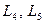 и называются точками либрации Лагранжа.
и называются точками либрации Лагранжа. , от которых не зависит функция Лагранжа, и позиционные координаты
, от которых не зависит функция Лагранжа, и позиционные координаты  , входящие явно в функцию Лагранжа, которая в этом случае имеет вид
, входящие явно в функцию Лагранжа, которая в этом случае имеет вид (1)
(1) (2)
(2)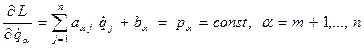 (3)
(3)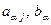 - компоненты матрицы
- компоненты матрицы  и вектора
и вектора  соответственно. Соотношения (3) представляют систему линейных алгебраических уравнений относительно неизвестных
соответственно. Соотношения (3) представляют систему линейных алгебраических уравнений относительно неизвестных  (4)
(4) - компоненты обратной матрицы диагонального минора
- компоненты обратной матрицы диагонального минора 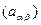 .
.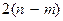 , описывающих изменение только позиционных координат. Определим функцию Рауса в виде
, описывающих изменение только позиционных координат. Определим функцию Рауса в виде (5)
(5)
 (6)
(6) (7)
(7) , циклические координаты находятся путем вычисления интегралов по времени
, циклические координаты находятся путем вычисления интегралов по времени (8)
(8)
 параметров – постоянных циклических интегралов.
параметров – постоянных циклических интегралов. циклических координат, и соответствующая функция Рауса не зависит явно от времени.
циклических координат, и соответствующая функция Рауса не зависит явно от времени. , при заданных значениях циклических интегралов, называется стационарным движением исходной системы уравнений Лагранжа.
, при заданных значениях циклических интегралов, называется стационарным движением исходной системы уравнений Лагранжа. (9)
(9)
 - масса материально точки, длина маятника и ускорение свободного падения,
- масса материально точки, длина маятника и ускорение свободного падения, 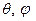 - сферические координаты. Угол
- сферические координаты. Угол  отсчитывается от нижнего положения равновесия, когда маятник висит по вертикали, а угол
отсчитывается от нижнего положения равновесия, когда маятник висит по вертикали, а угол  составляет вертикальная плоскость, в которой находится маятник и его точка подвеса, с аналогичной плоскостью в начальный момент движения. Угол
составляет вертикальная плоскость, в которой находится маятник и его точка подвеса, с аналогичной плоскостью в начальный момент движения. Угол  , а угол
, а угол  . Ясно, что координата
. Ясно, что координата 


 в положении равновесия является корнем последнего уравнения (стационарная точка измененной потенциальной энергии)
в положении равновесия является корнем последнего уравнения (стационарная точка измененной потенциальной энергии)  . Для определения устойчивости стационарного движения воспользуемся теоремой Лагранжа, для чего вычислим вторую производную в стационарной точке
. Для определения устойчивости стационарного движения воспользуемся теоремой Лагранжа, для чего вычислим вторую производную в стационарной точке (10)
(10)
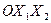 . В полярной системе координат кинетическая энергия, обобщенные импульсы и функция Гамильтона записываются в виде
. В полярной системе координат кинетическая энергия, обобщенные импульсы и функция Гамильтона записываются в виде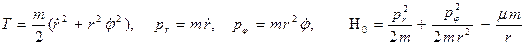


 . Выясним смысл постоянных величин
. Выясним смысл постоянных величин  и
и  в выражении полного интеграла. Постоянная
в выражении полного интеграла. Постоянная  , т. е. является модулем момента количества движения точки относительно притягивающего центра
, т. е. является модулем момента количества движения точки относительно притягивающего центра  направленного по неподвижной оси
направленного по неподвижной оси  . Постоянная
. Постоянная  при движении точки по кеплеровской эллиптической орбите. Найдем величину момента количества движения при движении точки по круговой орбите с данным значением полной энергии. В этом случае справедливы соотношения
при движении точки по кеплеровской эллиптической орбите. Найдем величину момента количества движения при движении точки по круговой орбите с данным значением полной энергии. В этом случае справедливы соотношения
 , т. е. равна модулю момента количества движения точки с заданной энергией при движении по круговой орбите.
, т. е. равна модулю момента количества движения точки с заданной энергией при движении по круговой орбите.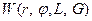 . Заметим, что в новых канонических переменных невозмущенный гамильтониан равен
. Заметим, что в новых канонических переменных невозмущенный гамильтониан равен  . Это означает, что канонические переменные
. Это означает, что канонические переменные  являются переменными действие, а сопряженные им угловые переменные
являются переменными действие, а сопряженные им угловые переменные  определяются по формулам
определяются по формулам (1)
(1) называются переменными Делоне, а канонические уравнения движения в новых переменных имеют вид
называются переменными Делоне, а канонические уравнения движения в новых переменных имеют вид (2)
(2)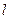 , являются постоянными.
, являются постоянными.
 после интегрирования получим уравнение Кеплера
после интегрирования получим уравнение Кеплера  . Здесь как было обозначено ранее
. Здесь как было обозначено ранее  - большая полуось и эксцентриситет орбиты,
- большая полуось и эксцентриситет орбиты,  - средняя и эксцентрическая аномалии соответственно.
- средняя и эксцентрическая аномалии соответственно. , определенная в (1), постоянна согласно каноническим уравнениям. Далее найдем
, определенная в (1), постоянна согласно каноническим уравнениям. Далее найдем

 - истинная аномалия, связанная с эксцентрической аномалией соотношением
- истинная аномалия, связанная с эксцентрической аномалией соотношением 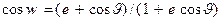 . Заметим, что согласно полученным формулам, радиус
. Заметим, что согласно полученным формулам, радиус  является функцией переменных
является функцией переменных  .
. , а второе задается неконсервативной силой
, а второе задается неконсервативной силой  , определяющей диссипацию энергии. Здесь
, определяющей диссипацию энергии. Здесь  малый параметр в том смысле, что соответствующие возмущающие силы малы по сравнению с основной силой гравитационного взаимодействия точки с притягивающим центром. Функция
малый параметр в том смысле, что соответствующие возмущающие силы малы по сравнению с основной силой гравитационного взаимодействия точки с притягивающим центром. Функция  (3)
(3)

 . Понятие медленной переменной означает, что скорость ее изменения пропорциональна величине малого параметра, т.е. мала по сравнению со скоростью изменения быстрой переменной, имеющей порядок единицы. Скорость изменения быстрой переменной претерпевает малые возмущения. Метод усреднения в данном случае означает замену правых частей уравнений (3) их средними значениями, имея в виду разложения периодических функций, стоящих в правых частях, в ряд Фурье по быстрой переменной
. Понятие медленной переменной означает, что скорость ее изменения пропорциональна величине малого параметра, т.е. мала по сравнению со скоростью изменения быстрой переменной, имеющей порядок единицы. Скорость изменения быстрой переменной претерпевает малые возмущения. Метод усреднения в данном случае означает замену правых частей уравнений (3) их средними значениями, имея в виду разложения периодических функций, стоящих в правых частях, в ряд Фурье по быстрой переменной 

 , а второе определяется диссипативной силой
, а второе определяется диссипативной силой  . Здесь
. Здесь  малые величины в том смысле, что соответствующие возмущающие силы малы по сравнению с основной силой гравитационного взаимодействия точки с притягивающим центром. Заметим, что возмущающие силы являются центральными силами, что влечет сохранения момента количества движения и сохраняет движение плоским. Подобного рода возмущения возникают при рассмотрении вязкоупругих свойств шарообразной деформируемой планеты, заменяющей материальную точку. Канонические уравнения возмущенного движения в переменных Делоне имеют вид
малые величины в том смысле, что соответствующие возмущающие силы малы по сравнению с основной силой гравитационного взаимодействия точки с притягивающим центром. Заметим, что возмущающие силы являются центральными силами, что влечет сохранения момента количества движения и сохраняет движение плоским. Подобного рода возмущения возникают при рассмотрении вязкоупругих свойств шарообразной деформируемой планеты, заменяющей материальную точку. Канонические уравнения возмущенного движения в переменных Делоне имеют вид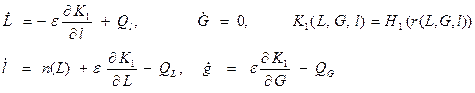 (1)
(1)
 . Переменная
. Переменная 

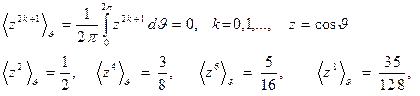


 , а эксцентриситет орбиты
, а эксцентриситет орбиты  стремится к нулю. В результате эволюции эллиптическая орбита стремится к круговой орбите.
стремится к нулю. В результате эволюции эллиптическая орбита стремится к круговой орбите.
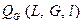 является периодической нечетной функцией относительно переменной
является периодической нечетной функцией относительно переменной 

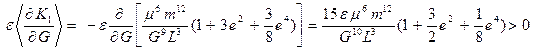

 неподвижна, а система координат
неподвижна, а система координат  связана с твердым телом. На теле в точке
связана с твердым телом. На теле в точке  на оси, лежащей в плоскости
на оси, лежащей в плоскости  , закреплен конек, лезвие которого направлено вдоль оси
, закреплен конек, лезвие которого направлено вдоль оси  и который скользит по неподвижной сфере с центром в точке
и который скользит по неподвижной сфере с центром в точке  , где
, где  – орт оси
– орт оси  . Скорость точки
. Скорость точки  (1)
(1) – угловая скорость твердого тела. Тело вращается вокруг неподвижной точки по инерции. На движение тела наложена неголономная связь (1). В точке контакта конька с неподвижной сферой на тело действует реакция неголономной связи – сила, направленная по оси с направляющим вектором
– угловая скорость твердого тела. Тело вращается вокруг неподвижной точки по инерции. На движение тела наложена неголономная связь (1). В точке контакта конька с неподвижной сферой на тело действует реакция неголономной связи – сила, направленная по оси с направляющим вектором 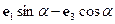 . Момент этой силы относительно неподвижной точки
. Момент этой силы относительно неподвижной точки  .
.
 (2)
(2) – тензор инерции тела относительно системы координат
– тензор инерции тела относительно системы координат  достигается соответствующим выбором угла
достигается соответствующим выбором угла  . Умножим уравнение (2) скалярно на вектор угловой скорости
. Умножим уравнение (2) скалярно на вектор угловой скорости  и получим первый интеграл – закон сохранения кинетической энергии
и получим первый интеграл – закон сохранения кинетической энергии (3)
(3) примет вид
примет вид (4)
(4) . Уравнения движения (2) в проекциях на оси
. Уравнения движения (2) в проекциях на оси  и
и  имеют вид
имеют вид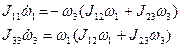 (5)
(5) (6)
(6) . В этом случае любая ось, проходящая через начало координат и лежащая в плоскости
. В этом случае любая ось, проходящая через начало координат и лежащая в плоскости  . Уравнения в вариациях имеют вид
. Уравнения в вариациях имеют вид (7)
(7) (8)
(8)
 (9)
(9) , которым соответствуют перманентные вращения вокруг одной и той же оси, но в разных направлениях. В зависимости от знака соответствующего корня (9) одно из этих вращений оказывается устойчивым, а второе – неустойчивым. Общая картина движения на плоскости переменных
, которым соответствуют перманентные вращения вокруг одной и той же оси, но в разных направлениях. В зависимости от знака соответствующего корня (9) одно из этих вращений оказывается устойчивым, а второе – неустойчивым. Общая картина движения на плоскости переменных  представлена на рисунке 2.
представлена на рисунке 2.
 – неустойчивое стационарное вращение,
– неустойчивое стационарное вращение,  – устойчивое стационарное вращение.
– устойчивое стационарное вращение. (10)
(10) (11)
(11)
 (12)
(12)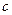 – произвольная постоянная. Правая часть уравнения (12) стремится к бесконечности, когда
– произвольная постоянная. Правая часть уравнения (12) стремится к бесконечности, когда  стремится к бесконечности. Следовательно,
стремится к бесконечности. Следовательно,  или
или  , когда время стремится к бесконечности. Знаки плюс или минус соответствуют двум возможным сценариям движения, отмеченным выше, когда движение тела стремится к стационарному вращению вокруг прямой
, когда время стремится к бесконечности. Знаки плюс или минус соответствуют двум возможным сценариям движения, отмеченным выше, когда движение тела стремится к стационарному вращению вокруг прямой  . В стационарном движении конек описывает окружность на сфере радиуса
. В стационарном движении конек описывает окружность на сфере радиуса 
 определяются из соотношений (10), (12).
определяются из соотношений (10), (12). и однопараметрическое семейство замкнутых областей
и однопараметрическое семейство замкнутых областей  ,
, 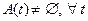 . Пусть
. Пусть  – масса материальных точек, образующих множество
– масса материальных точек, образующих множество  . Рассмотрим движение механической системы
. Рассмотрим движение механической системы  .
. – поле скоростей точек границы множества
– поле скоростей точек границы множества  , направленное по единичной внешней нормали
, направленное по единичной внешней нормали  к поверхности границы
к поверхности границы  . Тогда
. Тогда (1)
(1) – поверхностная мера, индуцированная пространственной мерой
– поверхностная мера, индуцированная пространственной мерой  . Например, в случае существования плотности
. Например, в случае существования плотности  справедливы равенства
справедливы равенства  , где
, где  – элемент площади поверхности
– элемент площади поверхности  , если
, если
 (2)
(2) – поле активных массовых сил. Уравнение (2) понимается в смысле равенства двух обобщенных функций, принадлежащих сопряженному пространству к пространству функций, непрерывных по времени и суммируемых по мере
– поле активных массовых сил. Уравнение (2) понимается в смысле равенства двух обобщенных функций, принадлежащих сопряженному пространству к пространству функций, непрерывных по времени и суммируемых по мере  .
. (3)
(3) , приложенных к точкам множества
, приложенных к точкам множества  , порождаемой изменением множества
, порождаемой изменением множества  (4)
(4) – часть границы
– часть границы  , а
, а  – часть границы
– часть границы  ,
,  – объемная плотность и элемент площади границы
– объемная плотность и элемент площади границы  .
.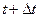 и приращение количества движения системы переменного состава (3)
и приращение количества движения системы переменного состава (3)


 как функции времени предполагаются гладкими на множестве
как функции времени предполагаются гладкими на множестве  может иметь разрыва первого рода. Далее с точностью до малых порядка
может иметь разрыва первого рода. Далее с точностью до малых порядка  представим полученное приращение в виде
представим полученное приращение в виде (5)
(5)


