
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Функция Ляпунова и теорема Ляпунова.Содержание книги
Поиск на нашем сайте
Пусть движение механической системы описывается уравнениями Лагранжа второго рода
Определитель матрицы Введем новые переменные
Для выполнения этой процедуры необходимо использовать обратную матрицу
Система (3) имеет нулевое решение и решения с начальными условиями из окрестности нуля. О. Решение Выбор нормы в определении устойчивости по Ляпунову не влияет на определяемое свойство движения, так как в конечномерном пространстве все нормы эквивалентны. Рассмотрим функцию а) б) в) О. Функция Т. Ляпунова. Если существует функция Ляпунова, то нулевое решение системы (3) устойчиво по Ляпунову. ◄Сфера Согласно определению функции Ляпунова (условие в) имеем неравенство
Допустим, что существует момент времени
МЕТОД РАУСА ИГНОРИРОВАНИЯ ЦИКЛИЧЕСКИХ КООРДИНАТ. УРАВНЕНИЯ РАУСА.
Допустим, что обобщенные координаты разбиваются на две группы: циклические координаты
Уравнения Лагранжа второго рода
имеют циклические первые интегралы
Здесь
где Следуя идее Рауса, получим систему дифференциальных уравнений порядка
Полный дифференциал функции Рауса представим двумя выражениями
Приравнивая коэффициенты при одинаковых дифференциалах, получим равенства
Заменим в
Заметим, что значения циклических интегралов в функции Рауса определяются начальными условиями движения и в дальнейшем не меняются. После того как найдено решение уравнений Рауса, т.е. зависимости
Как и в случае уравнений Лагранжа, из уравнений Рауса получается интеграл обобщенной энергии, если функции Лагранжа и Рауса не зависят явно от времени
Уравнения Рауса полностью аналогичны уравнениям Лагранжа и имеют те же свойства, только порядок этих уравнений на
|
||||
|
Последнее изменение этой страницы: 2016-08-10; просмотров: 362; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.226.169.169 (0.005 с.) |

 (1)
(1) положителен, поскольку он определяет положительно определенную квадратичную форму в выражении кинетической энергии системы.
положителен, поскольку он определяет положительно определенную квадратичную форму в выражении кинетической энергии системы. , с помощью которых уравнения (1) представим в виде, разрешенном относительно производных первого порядка
, с помощью которых уравнения (1) представим в виде, разрешенном относительно производных первого порядка (2)
(2) , которая существует в силу отмеченного выше ее свойства. Предположим. Что система (2) имеет решения, определенные на интервале от нуля до бесконечности, и пусть
, которая существует в силу отмеченного выше ее свойства. Предположим. Что система (2) имеет решения, определенные на интервале от нуля до бесконечности, и пусть  - частное решение системы (2). Используя замену переменных
- частное решение системы (2). Используя замену переменных  , представим систему уравнений (2) в форме
, представим систему уравнений (2) в форме (3)
(3) устойчиво по Ляпунову, если для любого
устойчиво по Ляпунову, если для любого  , существует
, существует  , такое, что для любого начального условия
, такое, что для любого начального условия  , где норма определяется, например, в виде
, где норма определяется, например, в виде  , решение
, решение  при всех значениях времени больше нуля.
при всех значениях времени больше нуля. в области
в области  со свойствами:
со свойствами: и
и  ;
;  ;
; непрерывна и
непрерывна и  только при
только при  (свойство положительной определенности);
(свойство положительной определенности); (свойство постоянства знака производной в силу уравнений движения).
(свойство постоянства знака производной в силу уравнений движения). является компактом, на котором функция
является компактом, на котором функция  достигает своей нижней грани
достигает своей нижней грани  . Существует такая окрестность нуля
. Существует такая окрестность нуля 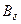 , во всех точках которой непрерывная функция
, во всех точках которой непрерывная функция  . Выберем начальное условие в области
. Выберем начальное условие в области  с этим начальным условием.
с этим начальным условием. .
. и
и  . Тогда
. Тогда  , что противоречит предыдущему неравенству. Противоречие доказывает теорему, поскольку траектория
, что противоречит предыдущему неравенству. Противоречие доказывает теорему, поскольку траектория  и, значит, остается в окрестности
и, значит, остается в окрестности  во все время движения.►
во все время движения.► , от которых не зависит функция Лагранжа, и позиционные координаты
, от которых не зависит функция Лагранжа, и позиционные координаты  , входящие явно в функцию Лагранжа, которая в этом случае имеет вид
, входящие явно в функцию Лагранжа, которая в этом случае имеет вид (1)
(1) (2)
(2)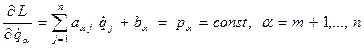 (3)
(3)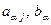 - компоненты матрицы
- компоненты матрицы  и вектора
и вектора  соответственно. Соотношения (3) представляют систему линейных алгебраических уравнений относительно неизвестных
соответственно. Соотношения (3) представляют систему линейных алгебраических уравнений относительно неизвестных  (4)
(4) - компоненты обратной матрицы диагонального минора
- компоненты обратной матрицы диагонального минора 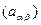 .
.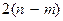 , описывающих изменение только позиционных координат. Определим функцию Рауса в виде
, описывающих изменение только позиционных координат. Определим функцию Рауса в виде (5)
(5)
 (6)
(6) первых уравнениях системы (2) частные производные функции Лагранжа согласно равенствам (6) на частные производные функции Рауса и получим систему уравнений Рауса
первых уравнениях системы (2) частные производные функции Лагранжа согласно равенствам (6) на частные производные функции Рауса и получим систему уравнений Рауса (7)
(7) , циклические координаты находятся путем вычисления интегралов по времени
, циклические координаты находятся путем вычисления интегралов по времени (8)
(8)
 параметров – постоянных циклических интегралов.
параметров – постоянных циклических интегралов.


