
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Относительные равновесия гибкой нити привязанной к спутнику на круговой орбитеСодержание книги
Поиск на нашем сайте
Рассмотрим вращающуюся систему координат Представим радиус вектор точки нити
где
Последние два условия в (22) являются кинематическими граничными условиями – условие закрепления нити на спутнике и динамическим граничным условием – равенство нулю натяжения нити на ее свободном конце. Здесь
Допустим, что справедлива оценка
Отбрасывая постоянную величину, получим функционал потенциальной энергии в виде
Первая и вторая вариации функционала (26) равны
На относительных положениях равновесия нити первая вариация обращается в нуль. Учитывая равенства (22), представим первую вариацию в виде
Последние два уравнения (28) имеют вид
Если Из выражения первой вариации в (27) следует, что поле сил, действующих на точки нити, имеет компоненты
Из уравнений (30) получим
Поскольку
где Исследуем устойчивость найденных конфигураций. Прежде всего, заметим, что рассматриваемая механическая система имеет первый интеграл – интеграл Якоби или обобщенный интеграл энергии. Умножим уравнение движения (23) на
так как
Устойчивость исследуемых положений равновесия будет иметь место, если потенциал
в этом случае является функционалом Ляпунова, и согласно теореме Ляпунова положения равновесия устойчивы. Покажем, что потенциал
Далее найдем
В результате вторая вариация потенциальной энергии примет вид
Следовательно, по теореме Ляпунова положения равновесия
|
|||||
|
Последнее изменение этой страницы: 2016-08-10; просмотров: 439; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.217.208.60 (0.01 с.) |

 . Ее угловая скорость постоянна и направлена по оси
. Ее угловая скорость постоянна и направлена по оси  . В точке
. В точке  помещена материальная точка, порождающая гравитационное поле с гравитационной постоянной
помещена материальная точка, порождающая гравитационное поле с гравитационной постоянной  , а на оси
, а на оси  на расстоянии
на расстоянии 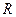 находится массивный спутник, к которому привязана однородная гибкая нерастяжимая нить длины
находится массивный спутник, к которому привязана однородная гибкая нерастяжимая нить длины 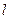 . Угловая скорость вращения системы координат соответствует угловой скорости вращения спутника по круговой орбите и равна
. Угловая скорость вращения системы координат соответствует угловой скорости вращения спутника по круговой орбите и равна 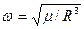 . Предполагается, что движение нити не возмущает движения спутника. Требуется найти положения равновесия нити относительно вращающейся системы координат и исследовать их устойчивость.
. Предполагается, что движение нити не возмущает движения спутника. Требуется найти положения равновесия нити относительно вращающейся системы координат и исследовать их устойчивость. (22)
(22) – орты соответствующих осей. Заметим, что ось
– орты соответствующих осей. Заметим, что ось 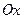 параллельна касательной к орбите движения спутника. Поскольку система координат
параллельна касательной к орбите движения спутника. Поскольку система координат  (23)
(23)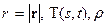 – натяжение и линейная плотность нити соответственно. Поля центробежных и гравитационных сил, действующие на точки гибкой нити, потенциальны, и их потенциал равен
– натяжение и линейная плотность нити соответственно. Поля центробежных и гравитационных сил, действующие на точки гибкой нити, потенциальны, и их потенциал равен (24)
(24) . Тогда отношение
. Тогда отношение  – малый параметр. Разложим потенциальную энергию (24) по малому параметру
– малый параметр. Разложим потенциальную энергию (24) по малому параметру  с точностью до членов второго порядка малости включительно. Имеем
с точностью до членов второго порядка малости включительно. Имеем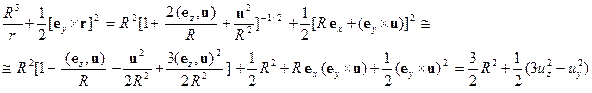 (25)
(25) (26)
(26)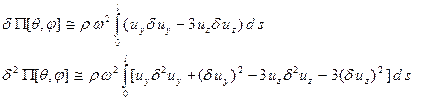 (27)
(27)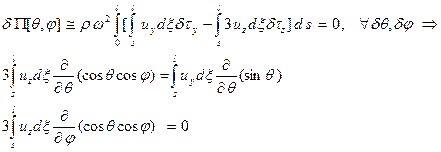 (28)
(28) (29)
(29)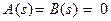 , то
, то  , и нить находится на оси
, и нить находится на оси  . Отсюда следует, что нить в положении равновесия должна располагаться либо в плоскости
. Отсюда следует, что нить в положении равновесия должна располагаться либо в плоскости  , либо на оси
, либо на оси 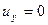 , то
, то  , и, поскольку
, и, поскольку 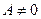 условия равновесия представляюся в виде
условия равновесия представляюся в виде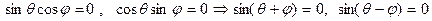 (30)
(30)
 , то
, то  и значения углов в положении равновесия равны
и значения углов в положении равновесия равны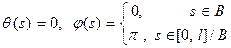 (31)
(31) – борелевское множество, полученное путем разбиения интервала
– борелевское множество, полученное путем разбиения интервала  на конечное или счетное число интервалов и дальнейшего отбрасывания любой их совокупности. Среди этих положений равновесия существуют две конфигурации нити, вытянутой вдоль оси
на конечное или счетное число интервалов и дальнейшего отбрасывания любой их совокупности. Среди этих положений равновесия существуют две конфигурации нити, вытянутой вдоль оси 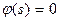 и угла
и угла  .
. и проинтегрируем полученное равенство по
и проинтегрируем полученное равенство по  от нуля до
от нуля до 
 . В результате получим
. В результате получим (32)
(32) имеет изолированный минимум в окрестности положений равновесия. Функционал
имеет изолированный минимум в окрестности положений равновесия. Функционал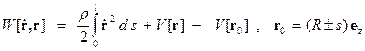
 (33)
(33)

 (33)
(33) устойчивы.
устойчивы.


