
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Кинетическая энергия твердого тела при вращении.Содержание книги
Поиск на нашем сайте
Рассмотрим вращение тела вокруг неподвижной оси, которую назовем осью Z (рис.). Линейная скорость точки с массой mi, равна vi = ωR, где R, —расстояние точки до оси Z. Для кинетической энергии i -й материальной точки тела получаем выражение:
Полная кинетическая энергия тела
Поскольку входящая сюда сумма представляет собой момент инерции относительно оси Z, получаем:
Вычислим работу, совершаемую внешней силой при вращении твердого тела. Элемент работы Последнее выражение есть момент внешней силы N, таким образом,
Полная работа может быть вычислена с помощью следующих формул:
Приведем в заключение формулу, описывающую кинетическую энергию тела, совершающего плоское движение — поступательное, со скоростью Vc и вращение с частотой ω):
Кинетическая энергия при плоском движении слагается из энергии поступательного движения со скоростью центра инерции тела и энергии вращения вокруг оси, проходящей через центр инерции. Релятивистская механика Механика Ньютона, или, как говорят, классическая механика, основана на принципе относительности Галилея, согласно которому все законы механики одинаковы во всех инерциальных системах отсчета. Математически принцип относительности в классической механике выражается с помощью преобразования Галилея — закона сложения скоростей при переходах от одной инерциальной системы отсчета к другой. Согласно этому закону скорость тела в неподвижной системе отсчета представляет собой сумму скорости тела по отношению к движущейся системе отсчета и скорости самой системы отсчета по отношению к неподвижной. Для всех наблюдаемых движений в природе, скорости которых малы по сравнению со скоростью света, этот закон выполняется с точностью, которая не давала оснований сомневаться в его справедливости вплоть до конца 19-го столетия. Измерения скорости света, проведенные с большой точностью в конце 19-го века, показали, однако, что закон сложения скоростей Галилея не выполняется для световых лучей. Скорость света, измеренная в движущейся системе координат, оказалась в точности такой же, как и для неподвижной системы отсчета. Таким образом, был установлен экспериментальный факт независимости скорости света от скорости движения источников либо приемников света. Другими словами, было установлено, что скорость света является абсолютной постоянной величиной, равной скорости света в пустоте с. Этот факт невозможно совместить с принципом относительности Галилея. Возникшее противоречие в классической механике привело А. Эйнштейна к необходимости допустить, что классическая механика справедлива лишь для скоростей малых по сравнению со скоростью света. При скоростях движения, сравнимых со скоростью света, справедлива созданная А. Эйнштейном механика специальной теории относительности, или, как ее называют, релятивистская механика. Если в релятивистской механике скорость света устремить к бесконечности, мы получим механику Ньютона. Принцип относительности Эйнштейна состоит в том, что не только законы механики, но и вообще все физические законы должны не зависеть от выбранной инерциальной системы отсчета. Поскольку распространение света представляет собой физический процесс, его скорость в пустоте должна быть неизменной в эквивалентных системах координат. Предположение об абсолютности скорости света приводит к целому ряду следствий, необычных и не наблюдаемых в условиях механики Ньютона. Одно из следствие постоянства скорости света состоит в отказе от абсолютного характера времени, который был привит в механике Ньютона. Нужно теперь допустить, что время течет по-разному в разных системах отсчета — события, одновременные в одной системе, окажутся неодновременными в другой. Рассмотрим две инерциальные системы отсчета K и K ', движущиеся относительно друг друга. Пусть в темной комнате, движущейся с системой K ', вспыхивает лампа. Поскольку скорость света в системе K ' равна (как и во всякой системе отсчета) c, то свет достигает обеих противоположных стен комнаты одновременно. Не то будет происходить с точки зрения наблюдателя в системе K. Скорость света в системе K также равна c, но так как стены комнаты движутся по отношению к системе K, то наблюдатель в системе K обнаружит, что свет коснется одной из стен раньше, чем другой, т.е. в системе K эти события являются неодновременными. Таким образом, в механике Эйнштейна относительны не только свойства пространства, но и свойства времени.
1.11.1. Преобразование Лоренца. Пусть имеются инерциальные системы отсчета K и K', показанные на рис. На рисунке предполагается, что движется система K', в то время как система K неподвижна. С таким же правом можно считать, что неподвижна система K', а система K движется относительно нее со скоростью — V.
Предположим, что происходит какое-то событие. В системе K. оно характеризуется значениями координат и времени x, у, z, t; в системе K' — значениями координат и времени x', y', z', t'. Найдем формулы связывающие нештрихованные значения со штрихованными. Из однородности пространства и времени следует, что эти формулы должны быть линейными. При показанном на рис. направлении координатных осей плоскость y' = 0 совпадает с плоскостью y = 0, а плоскость z' = 0 совпадает с плоскостью z = 0. Отсюда вытекает, что, например, координаты y и y' должны обращаться в нуль одновременно, независимо от значений других координат и времени. Это возможно лишь при условии, что y = α· y', где вследствие линейности уравнения α ‑ постоянная величина. Ввиду равноправности систем K и K' обратное преобразование должно иметь вид y' =α· y с тем же значением a, что и при прямом преобразовании. Перемножив оба соотношения, найдем, что α2 = 1, откуда α = ±1. Для одинаково направленных осей нужно взять α = +1. В результате находим, что y = y ' или y' = y. (1.104) Аналогичным образом получается формула z = z' или z' = z. (1.105) Из этих формул вытекает, что значения y и z не зависят от x' и t', откуда следует, что значения x' и t' не могут зависеть от y и t; соответственно значения x и t не могут зависеть от y' и z'. Это означает, что x и t являются линейными функциями только x' и t'. Из рис. следует, что точка O имеет координату x = O в системе K и x' = — Vt' в системе K'. Следовательно, выражение x' + Vt' должно обращаться в нуль одновременно с координатой x (когда x' + Vt' равно нулю, x' = — Vt'). Для этого линейное преобразование должно иметь вид x = γ(x' + Vt'), (1.106) где γ — константа. Точка O имеет координату x' = 0 в системе K' и x = V·t в системе K. Следовательно, выражение x — V·t должно обращаться в нуль одновременно с координатой x' (когда x — V·t = 0, то x = V·t). Для этого нужно, чтобы выполнялось соотношение x' = γ(x ‑ Vt). (1.107) В силу равноправности систем K и K' коэффициент γ в обоих случаях должен быть один и тот же. Теперь воспользуемся принципом постоянства скорости света. Начнем отсчет времени в обеих системах с того момента, когда начала координат O и O' совпадают. Предположим, что в момент t = t' = 0 в направлении осей x и x' посылается световой сигнал, который производит вспышку света на экране. Это событие (вспышка) характеризуется в системе K координатой x и временем t, а в системе K' — координатой x' и временем t', причем x = ct, x ' = ct '. (скорость c в обоих случаях одна и та же). Подставив эти значения x и x' в формулы, получим соотношения ct = γ(ct' + Vt') = γ(c + V) t', ct' = γ(ct ‑ Vt) = γ (c ‑ V) t. Перемножив эти соотношения и сократив обе части получившегося равенства на tt', придем к уравнению c2 = γ2(c2 ‑ V2). Отсюда
где β = V / c. (1.109) Подстановка найденного значения у в (1.106) и (1.107) приводит к формулам
Чтобы найти формулы преобразования времени, исключим из формул (1.110) координату x и разрешим получившееся уравнение относительно t. Затем исключим из формул (1.110) координату x' и разрешим получившееся уравнение относительно t'. В результате придем к формулам
Напишем вместе формулы (1.104), (1.105), (1.110) и (1.111), подразделив их на две группы:
Эти формулы называются преобразованиями Лоренца. По формулам (1.112) осуществляется переход от системы K' к системе K', по формулам (1.113)—переход от системы K к системе K' - Вследствие равноправности систем преобразования (1.112) и (1.113) отличаются лишь знаком перед V. Это отличие обусловлено тем, что система K' движется относительно системы K со скоростью V, в то время как система K движется относительно системы K' со скоростью — V. В преобразованиях Лоренца «перемешаны» координаты и время. Например, время t в системе K определяется не только временем t' в системе K', но также и координатой x'. В этом проявляется взаимосвязь пространства и времени. В пределе при V<<c преобразования Лоренца переходят в преобразования Галилея. Таким образом, различие в течение времени в разных инерциальных системах отсчета обусловлено существованием предельной скорости распространения взаимодействий. При скоростях много меньших скорости света (т. е. при β << 1) преобразования Лоренца практически не отличаются от преобразований Галилея. Следовательно, преобразования Галилея сохраняют значение для скоростей, малых по сравнению со скоростью света. При V > c выражения для x, t, x' и t' в формулах (1.112) и (1.113) становятся мнимыми. В этом проявляется то обстоятельство, что движение со скоростями, большими с, невозможно. Невозможна даже система отсчета, движущаяся со скоростью с, потому что при V = c знаменатели формул для x и t обращаются в нуль. Преобразованиям Лоренца можно придать симметричный вид, если написать их для x и ct, т. е. для величин одинаковой размерности. В этом случае формулы преобразований выглядят следующим образом:
Формулы для x и ct, а также для x' и ct' отличаются друг от друга только перестановкой соответствующих переменных. 1.11.2 Следствия из преобразований Лоренца Из преобразований Лоренца можно получить следствия, казалось бы, противоречащие нашему повседневному опыту. Это противоречие обусловлено тем, что наш опыт относится к процессам, протекающим со скоростями, весьма малыми по сравнению со скоростью света, и поэтому явления, которые мы сейчас рассмотрим, нами не ощущаются. Однако они с несомненностью присущи миру элементарных частиц, в котором движение со скоростями, близкими к c, представляет собой заурядное явление.
|
||||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 261; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.149.255.239 (0.006 с.) |


 .
. .
. (1.100)
(1.100) .
. . (1.101)
. (1.101) . (1.202)
. (1.202) (1.103)
(1.103)
 , (1.108)
, (1.108) ,
,  . (1.110)
. (1.110)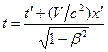 ,
,  (1.111)
(1.111)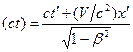 , (1.114)
, (1.114) .(1.115)
.(1.115)


