
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Основные представления кинетической теорииСодержание книги
Поиск на нашем сайте Теплота как форма энергии. Температура. Беспорядочное движение микроскопических частиц связано с содержанием в веществе теплоты — особой формы энергии. Эта связь достаточно очевидна на примере зависимости броуновского движения от количества сообщенного телу тепла. Макроскопическая характеристика теплового движения — температура. Температура есть мера содержащегося в теле тепла. Она же определяет направление перехода тепла — от более нагретого тела к менее нагретому. Если температуры тел одинаковы, то передачи тепла от одного тела к другому не происходит. Рассматривая теплоту как форму энергии, необходимо связать ее с кинетической энергией частиц. Чем больше нагрето тело, тем больше и кинетическая энергия его частиц. Таким образом, кинетическую энергию движения частиц так же, как и температуру, можно рассматривать как меру теплового движения. Естественно предположить, что обе эти величины связаны между собой. На существование такой связи указывает, например, аналогия между переходом теплоты от одного тела к другому и передачей кинетической энергии при столкновении упругих тел. Следует помнить, что температура — это макроскопическая характеристика тела, т. е. термодинамическая переменная, в то время как кинетическая энергия характеризует отдельную частицу. Поэтому температура должна быть связана со средней кинетической энергией, приходящейся на одну частицу в системе большого числа частиц. Среднюю кинетическую энергию частиц в системе, состоящей из N частиц, обозначим через < Ek > и определим ее следующим образом:
Если все частицы одинаковы, массу частицы можно вынести из-под знака суммы:
Будем считать что температура T ~ 2< Ek >/3 = m < v2 >/3. Для того чтобы выразить температуру в градусах, нужно ввести коэффициент пропорциональности, показывающий, сколько джоулей соответствует одному градусу. Он называется постоянной Больцмана и, как показывают измерения, равен 1,38·10‑23 Дж/К, где К означает градус Кельвина — единицу измерения температуры, используемую в физической шкале. Тогда соотношение между температурой в градусах и энергией в джоулях запишется в виде:
Принятая в физике шкала температур называется абсолютной шкалой, или шкалой Кельвина. В этой шкале температура замерзания воды, то есть 0°С, соответствует 273,15 градусов Кельвина, что обозначается 273,15 К. Согласно выражению (2.3) при T = 0 всякое тепловое движение частиц в веществе прекращается. Эта температура имеет название абсолютного нуля. Подчеркнем статистический характер определения температуры, поскольку она связана со средней энергией частиц. Поэтому можно говорить лишь о температуре системы достаточно большого числа частиц — макроскопической системы, и нельзя говорить о температуре одной или, допустим, десяти частиц. В процессе измерения температуры происходит обмен теплом между системой частиц — объектом измерения и измерительным прибором — термометром. Понятие температуры тела приобретает смысл в том случае, если обмен теплом между телом и прибором в процессе измерения температуры мало изменяет состояние тела. Для характеристики средней скорости движения частиц в системе обычно используется величина, называемая среднеквадратичной, или тепловой скоростью частиц. Средние тепловые скорости частиц существенно зависят от массы частицы
Для молекулы водорода H2 mH2 = 2· mH, а для молекулы кислорода mO2 = 32· mH, и отношение тепловых скоростей есть
Следовательно, молекулы кислорода движутся в 4 раза медленней. Порядок величины тепловой скорости атомов при T = 300 К, что соответствует комнатной температуре, составляет 103 м/с. Тепловые скорости броуновских частиц составляют по сравнению с ней ничтожные величины. Давление идеального газа Самой простой моделью макроскопического вещества является газ частиц. Газ представляет собой достаточно разреженную систему частиц. Частицы в газе находятся на значительном удалении друг от друга, совершая свободное движение и время от времени сталкиваясь друг с другом. Поэтому в первом приближении при рассмотрении газа можно не учитывать размеры и форму молекул, т. е. считать частицы материальными точками. По этой же причине можно пренебречь взаимодействием частиц на расстоянии, и к столкновениям частиц между собой и со стенками сосуда применять законы соударений упругих шаров. Такой газ называется идеальным. Модель идеального газа позволяет описать существенные черты поведения реального вещества.
Пусть в прямоугольном сосуде находится N молекул идеального газ». Стенки сосуда будем считать «идеально, отражающими». Примем,что при отражении от стенки скорость молекулы не меняется по величине, но меняется лишь по направлению. Если молекула, компонента скорости которой в направлении оси x равна vx, ударяется о стенку, то после отражения компонента ее скорости в этом направлении будет ‑ vx. Для изменения импульса в этом же направлении имеем D px = 2· m · vx. Долетев до противоположной стенки, молекула отразится от нее и снова ударится о первую стенку. Время между ударами составит Δ t = 2·l/ vx, а число ударов за 1 с будет
Но импульс, передаваемый за единицу времени стенке, равен силе, с которой данная молекула действует на стенку. Таким образом, i -я молекула действует на стенку с силой, компонента которой в направлении оси x Fix = mv2ix /l. Компонента силы, действующей вдоль оси x со стороны всех частиц, находящихся в сосуде, составит Перепишем это соотношение в виде Величина
Но l· S есть объем сосуда V. Значит: Таким образом, давление газа на стенку оказалось связанным со средним квадратом скорости смещения частиц в направлении нормали к стенке. Воспользуемся теперь соотношением v2i = v2ix + v2iy + v2iz. Усредняя его по всем частицам, получим < v2 > = < v2x >+ < v2y >+ < v2z >. Но все направления в пространстве равноправны, поэтому < v2x >= < v2y >= < v2z > и, следовательно, < v2x >= < v2 >/3. Выражение для давления принимает вид
Учтем, что величина m < v2 >/2 равна средней кинетической энергии поступательного движения молекул < Ek >. Окончательно получим:
Это соотношение одно из основных в кинетической теории газов.
|
|||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 260; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.138.67.56 (0.005 с.) |

 . (2.1)
. (2.1) . (2.2)
. (2.2)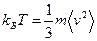 или
или 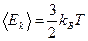 . (2.3)
. (2.3) . (2.4)
. (2.4)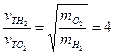
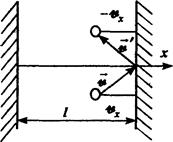
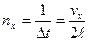 . За 1 с молекула сообщит стенке импульс с компонентой вдоль оси x
. За 1 с молекула сообщит стенке импульс с компонентой вдоль оси x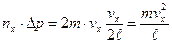 .
. .
. .
. есть средний квадрат компоненты скорости молекулы в направлении оси x. Поэтому
есть средний квадрат компоненты скорости молекулы в направлении оси x. Поэтому 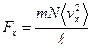 . Если эту силу разделить на площадь стенки S, то получим величину давления на стенку:
. Если эту силу разделить на площадь стенки S, то получим величину давления на стенку: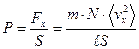 . (2.5)
. (2.5) .
. .
. . (2.6)
. (2.6)


