
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Упругое и неупругое взаимодействияСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
При взаимодействии тел друг с другом изменяются их энергия и импульс. Это изменение, однако, может происходить по-разному. Когда речь идет о взаимодействии массивных тел, которые состоят из большого числа частиц, атомов или молекул, имеет смысл наряду с кинетической и потенциальной энергией говорить о внутренней энергии тела. Внутренняя энергия — это энергия всех частиц, составляющих тело, при заданных его температуре и объеме. В результате взаимодействия тела с другими телами может измениться его температура, а также (необратимым образом) его объем. Ясно, что эти изменения связаны с расходом энергии, т. е. в результате взаимодействия тела с внешними объектами меняется его внутренняя энергия. Такое взаимодействие является неупругим. Оно, очевидно, не сохраняет полной механической энергии тела —суммы кинетической и потенциальной. Напротив, если в результате взаимодействия внутреннее состояние тела не меняется, взаимодействие является упругим. В процессе упругого взаимодействия выполняется закон сохранения механической энергии. Рассмотрим в связи с этими соображениями столкновения двух тел. Столкновение тел заключается в их кратковременном взаимодействии, происходящем при соприкосновении тел. Поскольку вне этого момента времени тела не взаимодействуют, их потенциальная энергия относительно друг друга равна нулю. Взаимодействие при столкновении состоит, таким образом, в передаче от одного тела другому импульса и кинетической энергии. Рассмотрим удар двух шаров, центры которых движутся вдоль одной прямой, т. е. центральный удар. Пусть массы шаров m1 и m2, скорости до удара v1, и v2, после удара u1 и u2. Для определенности возьмем случай движения шаров, изображенный на рис..
Центральный удар шаров Сначала рассмотрим упругий удар шаров. В применении к данной задаче закон сохранения импульса системы шаров имеет вид: m1v1 + m2v2 = m1u1 + m2u2, 1.50) т.е. импульс системы до столкновения равен импульсу системы после столкновения. Закон сохранения энергии дает
Перенося члены, относящиеся к первому шару влево, а ко второму шару вправо, и разделив одно из полученных уравнений на другое, находим:
Решая полученную систему уравнений совместно, получаем:
Исследуем полученный результат в частных случаях. 1. Соударение одинаковых шаров. Тогда m1 = m2 и u 1 = v 2, u 2 = v 1. (1.54) т. е. при упругом центральном ударе двух тел одинаковой массы они просто обмениваются скоростями. Если, в частности, до удара второй шар покоился (v2 = 0), то после удара остановится первый шар (u1 = 0), а второй будет двигаться с той же скоростью и в том же направлении, в котором двигался до удара первый шар (u2 = v1,). 2. Удар шара о массивную стенку. В этом случае m2 >> m1 и приближенно будем иметь:
Как видно отсюда, скорость массивного тела после удара меняется незначительно. В результате удара стенке передается значительный импульс, но передача энергии при ударе сравнительно мала:
Если стенка была первоначально неподвижна (v2 = 0), то упруго ударившийся о нее шарик малой массы отскочит обратно практически с теми же скоростью (u1 = ‑ v1) и энергией. При ударе о движущуюся стенку происходит обмен энергией между стенкой и шариком тем больший, чем больше скорость стенки. В зависимости от направления движения стенки (v2 больше или меньше 0) шарик отскакивает от стенки с большими или меньшими, чем до столкновения, кинетической энергией и импульсом. Рассмотрим теперь абсолютно неупругий удар шаров. При таком ударе энергия налетающего шара полностью расходуется на изменение внутренней энергии другого шара и на сообщение ему некоторой скорости. Закон сохранения механической энергии не выполняется, и для определения скорости после удара достаточно закона сохранения импульса. m1v1 + m2v2 =(m1 + m2) u1, (1.56) откуда
Потеря механической энергии, перешедшей во внутреннюю энергию шаров, равна разности энергий до и после удара:
Подставляя сюда (1.57), находим
Если ударяемое тело было первоначально неподвижно (v2 = 0), то
Когда неподвижное тело имеет большую массу (m2 > m1), то почти вся кинетическая энергия переходит при ударе во внутреннюю анергию. Напротив, при m1 >> m2 изменение внутренней энергии мало и большая часть кинетической энергии идет на сообщение движения ударяемому телу. Сила упругости В законе Ньютона сила есть физическая величина, характеризующая действие одного тела на другое и сообщающая последнему ускорение. Сила может также приводить к изменению формы и объема тела. В этом случае происходит деформация тела. Что происходит в действительности при приложении силы — ускорение тела или его деформация — определяется самими свойствами тела. Более того, свойства тела определяют и характер деформации, которая может быть упругой и неупругой. Неупругая деформация характеризуется тем, что она не исчезает после снятия нагрузки. С неупругой деформацией связано изменение внутренней энергии тела. Напротив, если после снятия нагрузки деформация исчезает и тело возвращается к своей прежней форме, то деформация является упругой. Сила, возвращающая тело к своей прежней форме, — упругая сила. Как показывает опыт, упругая сила пропорциональна созданной в теле деформации. Соответствующий закон называется законом Гука:
F =- k x, (1.62) где k — коэффициент пропорциональности, а x — величина деформации тела (рис.): x > 0 при растяжении тела, x < 0 — при сжатии. Вычислим работу, совершаемую против упругой силы, при деформации одномерного стержня на dx:
Эта работа идет на изменение взаимного расположения отдельных частей тела, т. е. на изменение его потенциальной энергии. Следовательно, зависимость потенциальной энергии стержня имеет вид:
График зависимости U от x показан на рис.
Сила трения Наряду с силами тяготения и упругими силами существуют силы, обусловленные молекулярными взаимодействиями между соприкасающимися поверхностями тел и зависящие от их скоростей. Опыт показывает, что сила трения, действующая на тело, направлена в сторону, противоположную его скорости. Поэтому работа сил трения всегда отрицательна: dA = F TP · dr = F TP · v · dt = ‑ FTP · v · dt = ‑ FTP · dr. (1.65) Следовательно, при наличии в системе сил трения полная механическая энергия системы уменьшается, переходя в другие формы энергии, а силы, приводящие к потере (диссипации) энергии, называются диссипативными. Таким образом, силы трения являются диссипативными силами. При наличии силы трения закон Ньютона приобретает вид:
откуда
Если сила трения уравновешивает внешнюю силу, то тело будет двигаться равномерно и прямолинейно. Примером является свободное падение тела с учетом сопротивления воздуха, которое происходит с постоянной скоростью, зависящей от формы и размеров тела.
Рассмотрим трение скольжения (рис.). Силу тяжести P можно разложить на две составляющие F и N, соответственно параллельно и перпендикулярно направлению скольжения. Сила N, прижимающая тело к поверхности, увеличивает взаимодействие между трущимися поверхностями. Сила трения скольжения противоположна направлению силы, заставляющей тело скользить. В то время как сила F = P sin a, сила трения FTP = μ· N = μ· P · cosα. (1.68) где μ — коэффициент трения, зависящий от формы и состояния соприкасающихся поверхностей, а также от скорости движения. Центр инерции
Импульс замкнутой механической системы имеет различные значения по отношению к различным инерциальным системам отсчета. Если система отсчета K' движется относительно системы K со скоростью V, то скорости частиц v'α и vα в этих системах связаны соотношением vα = v'α + V. Поэтому связь между значениями P и P' импульса в этих системах дается формулой:
или
Всегда можно подобрать такую систему отсчета K', в которой полный импульс обращается в нуль. Положив P' =0, находим, что скорость этой системы отсчета
Если полный импульс механической системы равен нулю, то говорят, что она покоится относительно соответствующей системы координат. Скорость V имеет смысл скорости движения механической системы как целого с отличным от нуля импульсом. Связь между импульсом P и скоростью V системы как целого такая же, какая была бы между импульсом и скоростью одной материальной точки с массой, равной сумме масс в системе, Правая сторона формулы (1.71) может быть представлена как полная производная по времени от выражения:
Можно сказать, что скорость V системыкак целого есть скорость перемещения в пространстве точки, радиус-вектор которой дается формулой (1.72). Такая точка является центром инерции системы. Закон сохранения импульса замкнутой системы можно сформулировать как утверждение о том, что ее центр инерции движется прямолинейно и равномерно. Это есть обобщение закона инерции для свободной материальной точки. Энергию покоящейся как целое механической системы обычно называют ее внутренней энергией Eвн. Она состоит из кинетической энергии движения частиц относительно друг друга и потенциальной энергии их взаимодействия. Полная же энергия системы, движущейся как целое со скоростью V,
|
|||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 1839; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.41 (0.01 с.) |


 . (1.51)
. (1.51) ,
,  .
. , (1.52)
, (1.52) . (1.53)
. (1.53) (1.55)
(1.55) .
. .
. . (1.57)
. (1.57) . (1.58)
. (1.58) . (1.59)
. (1.59) (1.60)
(1.60) 1.61)
1.61)
 (1.63)
(1.63) . (1.64)
. (1.64)
 (1.66),
(1.66), (1.67)
(1.67)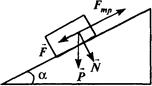
 (1.69)
(1.69) (1.70)
(1.70) . (1.71)
. (1.71) .
. (1.72)
(1.72) (1.73)
(1.73)


