
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Изучение упругого и неупругого столкновения телСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
САНКТ-ПЕТЕРБУРГ 2012 г. РАБОТА 2. ИЗУЧЕНИЕ УПРУГОГО И НЕУПРУГОГО СТОЛКНОВЕНИЯ ТЕЛ
Цель работы – исследовать упругое и неупругое столкновение двух тел; изучить законы сохранения импульса и энергии; выполнить сравнительную оценку экспериментальных и теоретических данных.
Теоретические основы лабораторной работы Удар (столкновение, соударение) – взаимодействие тел, при котором происходит их деформация, то есть изменение их формы или размера. Длительность взаимодействия при этом равна нулю (мгновенное событие). Применяется в качестве модели для описания реальных взаимодействий, длительностью которых можно пренебречь в условиях данной задачи. Предельные виды:абсолютно упругий и абсолютно неупругий удар. Абсолютно упругий - удар, после которого форма и размеры тел восстанавливаются полностью до состояния, предшествующего столкновению. При этом ударе механическая энергия тел не переходит в другие, немеханические виды энергии. При таком ударе кинетическая энергия движения соударяющихся тел переходит в потенциальную энергию упругой деформации, а затем потенциальная энергия упругой деформации снова переходит в кинетическую энергию. Тела разлетаются со скоростями, величина и направление которых определяется законом сохранения полной механической энергии и законом сохранения импульса. Абсолютно неупругий удар – столкновение двух тел, после которого форма и размеры тел не восстанавливаются.При этом ударе кинетическая энергия полностью или частично превращается во внутреннюю энергию, приводя к повышению температуры тел. После удара столкнувшиеся тела либо движутся вместе с одинаковой скоростью, либо покоятся. При абсолютно неупругом ударе выполняется только закон сохранения импульса. Основные характеристики центрального удара двух шаров. Удар называется центральным, если шары до удара движутся вдоль прямой, проходящей через их центры масс. Законы сохранения справедливы для замкнутых механических систем (внешние силы отсутствуют) или для незамкнутых, в которых внешние силы, приложенные к телам системы, уравновешивают друг друга. Будем предполагать, что шары образуют замкнутую механическую систему. Абсолютно неупругий удар В соответствии с законом сохранения импульса
Вектор скорости
Величина скорости
Здесь знак (+) соответствует движению тел в одном направлении, а знак (-) – движению тел навстречу друг другу. Количество механической энергии перешедшей во внутреннюю энергию (в тепло) равно разности энергий до удара (W10 + W20) и после удара W:
здесь: m1, m2 – массы шаров; Частные случаи. 1. Ударяемое тело (m2) неподвижно (u20=0). Из формулы (2.3) следует:
Из формул (2.4) и (2.5) можно получить следующую зависимость количества тепла QT от отношения масс (m2 / m1)
2. Масса ударяемого тела велика по сравнению с налетающим телом, (m2 >>m1). Из (2.4) следует:
То есть, в этом случае почти вся кинетическая энергия переходит в тепло. 3. Масса ударяемого тела мала по сравнению с налетающим телом, (m2<< m1) Из формулы (2.5) получаем:
Соответственно из формулы (2.4) получаем, что Q»0, то есть, кинетическая энергия движущегося шара переходит в кинетическую энергию системы Абсолютно упругий удар. Используя закон сохранения импульса и закон сохранения энергии можно записать систему уравнений
Решение системы этих двух уравнений позволяет получить следующие формулы для скоростей шаров после удара
Частные случаи. 1. Массы шаров одинаковы, (m1=m2). Из формул (2.11) и (2.12) в этом случае получим:
То есть, шары при соударении обмениваются скоростями. 2. Один из шаров, например, второй неподвижен (u20=0). После удара он будет двигаться со скоростью равной скорости первого шара (и в том же направлении), а первый шар остановится. 3. Удар шара о массивную стенку массой m2, (m2>>m1). Из формул (2.11) и (2.12) получим:
4. Скорость стенки v20 остаётся неизменной (стена неподвижна, u20=0). Ударившийся о стену шарик отскочит обратно практически с той же скоростью, то есть В данной лабораторной работе объектами взаимодействия являются лабораторные тележки.
|
||
|
Последнее изменение этой страницы: 2016-04-08; просмотров: 1041; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.156 (0.01 с.) |


 (2.1)
(2.1) (2.2)
(2.2) (2.3)
(2.3) (2.4)
(2.4)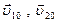 , W10 , W20 - скорости и энергии шаров до удара;
, W10 , W20 - скорости и энергии шаров до удара;  , W - скорость и энергия обоих шаров после удара.
, W - скорость и энергия обоих шаров после удара. (2.5)
(2.5) (2.6)
(2.6) (2.7)
(2.7) (2.8)
(2.8)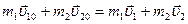 (2.9)
(2.9)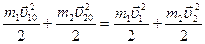 (2.10)
(2.10) (2.11)
(2.11) (2.12)
(2.12) - скорости шаров после удара.
- скорости шаров после удара.
 ,
, 
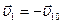 .
.


