
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Теория активных столкновенийСодержание книги
Поиск на нашем сайте В теории активных столкновений считается, что акт превращения начальных веществ в конечные продукты совершается в момент столкновения активных молекул и протекает мгновенно. При этом молекулы рассматриваются как бесструктурные частицы, хотя в действительности химические реакции происходят путем постепенной перестройки молекул и перераспределения энергии между химическими связями. Чтобы произошла реакция, частицы в момент столкновения должны: – обладать некоторым минимальным избытком энергии, называемым энергией активации (Е); – должны быть правильно ориентированы в пространстве относительно друг друга. Рассмотрим кинетику бимолекулярной реакции в газовой фазе. Согласно молекулярно-кинетической теории газов полное число столкновений Z 12 за 1 сек в 1м3, если в системе реагируют молекулы двух разных видов, рассчитывается по уравнению:
где n 1, n 2 – число молекул в 1 единице объема (см3); R 1=8,314∙107 эрг/(моль·К); размерность выражения: Если между молекулами газа нет взаимодействия и молекулы считаются сферами, то сечение столкновения можно рассчитать через радиусы молекул:
Притяжение между молекулами увеличивает сечение столкновения: Оценка эффективного диаметра стокновения возможна по вязкости газов или плотности жидкостей и твердых тел. 1. По вязкости газов:
где 2. По значениям мольных объемов жидкостей или твердых веществ:
3. В некоторых случаях эффективный диаметр столкновения можно оценить приближенно, используя соотношение:
Число двойных столкновений между молекулами одного сорта равно:
Число столкновений при n A= n B =1 называют частотой столкновений z 0:
Так как Эта величина равна вероятности столкновения двух частиц в единицу времени в единице объема. Число столкновений активных молекул Zа, рассчитанное на основе закона распределения Максвелла-Больцмана, определяется соотношением:
где Z 12 - полное число столкновений, Е * - истинная энергия активации реакции. Отношение
представляет собой долю активных столкновений из общего числа столкновений молекул. Так как для бимолекулярной реакции с участием молекул двух разных видов каждое столкновения активных молекул должно приводить к исчезновению одной молекулы данного вида, то скорость реакции можно рассчитать исходя из числа активных столкновений:
Подстановка уравнений (4.199) и (4.202) в (4.203) позволяет получить выражения для скорости бимолекулярной реакции на основе модели активных столкновений: а) для молекул разного вида
б) для молекул одного вида
С другой стороны, согласно основному постулату химической кинетики, скорость реакции выражается уравнением:
где n 1, n 2 – концентрации газов выраженные через число частиц в 1 см3. Для взаимодействия одинаковых и неодинаковых молекул константа скорости равна:
Константа скорости по теории активных столкновений может иметь разную размерность. Формулы пересчета констант: k [ = k ∙6∙10-2 ∙NA [ С учетом выражения для частоты столкновения (4.200) вместо (4.207) можно записать формулы для расчета константы скорости: а) для молекул разного вида
б) для молекул одного вида
Уравнения (4.208) и (4.208а), где константа скорости рассчитана через число двойных соударений, называют уравнением Таутца – Льюиса. Оно применимо к бимолекулярным реакциям, как в растворе, так и в газовой фазе. Теория активных столкновений может быть применена для оценки величин констант скоростей мономолекулярных реакций. В этих реакциях, приобретение молекулами избыточной энергии также происходит через бимолекулярные столкновения. Поэтому выражение для скорости реакции будет иметь тот же вид, что и для скорости бимолекулярной реакции с участием одинаковых молекул:
Согласно основному постулату химической кинетики скорость мономолекулярной реакции равна:
В этих уравнениях NА = 6,022·1023 моль-1– число Авогадро; р – парциальное давление. Если давление выражено в атм, то R 3 = 82 см3∙атм /моль×К, если давление выражено в Па, то R 3 = 82·1,013×105 см3∙Па /моль×К. Сравнение скоростей реакций, рассчитанных по опытным данным, показывает, что в большинстве случаев Первоначально предполагали, что стерический фактор связан с необходимой ориентацией сталкивающихся молекул и характеризует вероятность определенной геометрической конфигурации частиц при столкновении. В дальнейшем было установлено, что существует еще ряд причин, по которым С учетом стерического фактора выражение для константы скорости на основе модели активных столкновений имеет вид:
Сравнивая уравнения (4.208) и (4.209) с уравнением Аррениуса (4.65) получим уравнение для расчета предэкспоненциального множителя по теории активных столкновений: а) для молекул разного вида
б) для молекул одного вида
в) для мономолекулярных реакций
Из сравнения уравнения Аррениуса (4.65) с уравнением Траутца-Льюиса следует, что в уравнении Аррениуса предэкспоненциальный множитель не зависит от температуры, а в уравнении Траутца-Льюиса - пропорционален
Теория активных столкновений, вводя понятие о стерическом факторе Р, не дает способов расчета этого параметра. Оценку значения Р обычно проводят путем сравнения значений констант скоростей реакций, рассчитанных по уравнению Аррениуса (4.65) -
Стерический фактор можно также рассчитать по уравнению
где
|
||
|
Последнее изменение этой страницы: 2016-12-10; просмотров: 519; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.01 с.) |

 (молекул/см3∙с), (4.194)
(молекул/см3∙с), (4.194) – эффективное сечение столкновения (
– эффективное сечение столкновения ( ); d 12 =1/2 (d 1 + d 2) – эффективный диаметр столкновений;
); d 12 =1/2 (d 1 + d 2) – эффективный диаметр столкновений;  ,
,  – молекулярные массы реагирующих молекул, г/моль;
– молекулярные массы реагирующих молекул, г/моль; =
=  .
. =
= 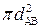 (4.195)
(4.195) , а отталкивание – уменьшает его:
, а отталкивание – уменьшает его:  .
. , (4.196)
, (4.196) – вязкость газа, г/см·с; М – молекулярная масса, г/моль; Т – абсолютная температура, К.
– вязкость газа, г/см·с; М – молекулярная масса, г/моль; Т – абсолютная температура, К. . (4.197)
. (4.197) (4.198)
(4.198) (молекул/см3∙с). (4.199)
(молекул/см3∙с). (4.199) [1]. (4.200)
[1]. (4.200) , то размерность частоты стокновений – см3/ (молекул ∙с).
, то размерность частоты стокновений – см3/ (молекул ∙с).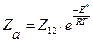 (молекул/см3∙с), (4.201)
(молекул/см3∙с), (4.201) (4.202)
(4.202) или
или  . (4.203)
. (4.203) ; (4.204)
; (4.204) . (4.205)
. (4.205) , (4.206)
, (4.206) см3/ молекул ∙с. (4.207)
см3/ молекул ∙с. (4.207) ] = k∙NA [
] = k∙NA [  ] = k∙ 10-3[
] = k∙ 10-3[  ] = k∙ 10-3 ∙NA [
] = k∙ 10-3 ∙NA [  ] =
] = ].
]. см3/моль×с; (4.208)
см3/моль×с; (4.208)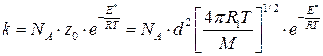 см3/моль×с, (4.208а)
см3/моль×с, (4.208а) молекул/см3×с. (4.209)
молекул/см3×с. (4.209) . Тогда, выражение для константы скорости мономолекулярной реакции, рассчитанное с использованием теории активных столкновений будет иметь вид:
. Тогда, выражение для константы скорости мономолекулярной реакции, рассчитанное с использованием теории активных столкновений будет иметь вид: с-1. (4.209а)
с-1. (4.209а)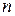 - число молекул в единице объема рассчитывается по формуле:
- число молекул в единице объема рассчитывается по формуле:  .
. . Для согласования опытных и расчетных данных Дж. Христиансен (1924 г.) ввел поправочный множитель, названный стерическим фактором Р.
. Для согласования опытных и расчетных данных Дж. Христиансен (1924 г.) ввел поправочный множитель, названный стерическим фактором Р. см3/ молекул ∙с. (4.210)
см3/ молекул ∙с. (4.210) см3/моль×с; (4.211)
см3/моль×с; (4.211)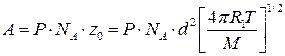 см3/моль×с, (4.212)
см3/моль×с, (4.212) с-1. (4.212а)
с-1. (4.212а) . Из этого следует, что величина истинной энергии активации Е * по физическому смыслу полностью аналогична аррениусовской энергии активации
. Из этого следует, что величина истинной энергии активации Е * по физическому смыслу полностью аналогична аррениусовской энергии активации 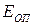 , но по численному значению отличается от неё. Сравнивая эти уравнения легко показать, что опытная энергия активации связана с теоретической (
, но по численному значению отличается от неё. Сравнивая эти уравнения легко показать, что опытная энергия активации связана с теоретической ( ) уравнением
) уравнением . (4.213)
. (4.213) и по уравнениям теории активных столкновений (4.208) и (4.209) -
и по уравнениям теории активных столкновений (4.208) и (4.209) - 
 . (4.214)
. (4.214) , (4.215)
, (4.215) – предэкспоненциальный множитель в уравнении Аррениуса.
– предэкспоненциальный множитель в уравнении Аррениуса.


