
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Экспериментальное определение ЭДССодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
ЭДС гальванического элемента определяется уравнением Нернста только в условиях обратимого протекания в нем процессов. Это соответствует протеканию через элемент бесконечно малого тока (бесконечно медленное проведение процессов). Поэтому измерение ЭДС электрохимических цепей стремятся проводить в условиях, когда ток через элемент не протекает или этот ток бесконечно мал. В условиях протекания через гальванический элемент значительных токов происходит существенное уменьшение ЭДС элемента, которое определяется многими факторами, в том числе, кинетикой электродных реакций и условиями диффузии веществ внутри элемента. Для измерения ЭДС электрохимических цепей пользуются компенсационной схемой или потенциометрами с достаточно большим входным сопротивлением (сотни МОм). Часто в лабораторных условиях для измерения ЭДС элементов вместо потенциометров используются высокоомные цифровые вольтметры.
Компенсационный метод заключается в том, что неизвестная ЭДС гальванического элемента компенсируется известной ЭДС какого-либо элемента (рис. 5). Моменту компенсации отвечает отсутствие тока в цепи. В качестве вспомогательного элемента, с хорошо известной и устойчивой ЭДС, наиболее часто применяется нормальный элемент Вестона.
Термодинамика обратимых электрохимических систем Изменение энергии Гиббса для реакции, обратимо протекающей в гальваническом элементе, можно записать Dr G = – zFЕ. (3.46) Запишем также уравнение Гиббса — Гельмгольца
Тогда
Учитывая, что для химической реакции справедливо
Получим
Таким образом, температурный коэффициент ЭДС связан с изменением энтропии химической реакции, протекающей в гальваническом элементе. На практике, измеряя ЭДС гальванического элемента при разных температурах и постоянном давлении, мы можем определить как изменение энтропии, так и изменение энтальпии соответствующей химической реакции.
Потенциометрия Потенциометрия — метод исследования, в основе которого лежат термодинамические соотношения между ЭДС электрохимических цепей, с одной стороны, и физико-химическими параметрами растворов и химических реакций с другой. Потенциометрию используют для определения
— pH растворов, — констант гидролиза солей, — констант диссоциации кислот и оснований, — произведений растворимости малорастворимых соединений, — констант устойчивости комплексов, — коэффициентов активности ионов в растворах, — термодинамических характеристик химических реакций — и т. д. Например, ионное равновесие в растворе характеризуется соответствующими термодинамическими константами. Например, для малорастворимого соединения, диссоциирующего по уравнению AB равновесие характеризуется произведением растворимости:
Для определения произведения растворимости можно составить гальванический элемент A | AB | DB || AC | A, где AC и DB — хорошо растворимые соли соответствующего катиона (A+) и аниона (B–), A+ | A — электрод первого рода, а B– | AB, A — электрод второго рода. На электродах будут протекать следующие реакции: (1) A+ + e– (2) AB + e– Запишем уравнения Нернста для этих электродов.
Электрод второго рода можно представить как электрод первого рода, только с очень малой концентрацией иона металла, которая будет зависеть от концентрации аниона, образующего с ним малорастворимое соединение. Тогда, учитывая выражение для произведения растворимости, получим
Выражение для ЭДС этого элемента будет
Таким образом, произведение растворимости малорастворимого соединения связано с ЭДС рассмотренного элемента, и для его определения необходимо измерить ЭДС элемента при известных активностях иона металла (A+) в растворе первого электрода и аниона B– в растворе второго. Для определения других термодинамических констант необходимо составлять соответствующие электрохимические цепи и измеряя их ЭДС при известных активностях потенциалопределяющих веществ вычислять значение констант. Рассмотрим, например, как методом потенциометрии можно оценить термодинамические функции химических реакций
1) изменение энергии Гиббса:
DG = - zFE; (3.56)
2) изменение энергии Гельмгольца: DA = - zFE - Dn RT, (3.57) где Dn – изменение числа молей газообразных веществ, участвующих в реакции; 3) изменение энтропии можно оценить, зная зависимость ЭДС элемента от температуры: DS= zF где Например, зависимость ЭДС от температуры можно описать уравнением:
При изменении температуры ЭДС элемента может оставаться постоянной величиной, увеличиваться или уменьшаться в зависимости от величины и знака температурного коэффициента ЭДС. 4) изменение внутренней энергии системы: DU = Qv = - zF (E-T 5) тепловой эффект химической реакции: DH = Qp = - zF(E - T Если реакция в элементе протекает без выделения газов, то можно принять, что DH = DU, (Qp = Qv). (3.62) Приведённые выше выражения можно использовать и для вычисления стандартных величин (DG°, DA°, DS°, DH°, DU°). Если стандартные термодинамические потенциалы определяются по справочным данным, то возможно решение обратной задачи, то есть определение стандартной ЭДС. При этом используются соотношения:
Примеры решения задач Пример 1. Вычислить термодинамические параметры (DG°, DA°, DS°, DH°, DU°) химической реакции Cd + Hg2SO4= 2 Hg + CdSO4, осуществляемой при работе нормального элемента Вестона. Зависимость ЭДС этого элемента от температуры выражается уравнением:
Решение. Нормальный элемент Вестона представляет собой электрохимический элемент (-) Сd(Hg), CdSO4·8/3 H2O½CdSO4aq нас. ½Hg2SO4, Hg (+) Покажем, что итогом работы этого элемента является химическая реакция, записанная в условии задачи. Реакции, протекающие на электродах: а) на отрицательном Cd = Cd2+ + 2e; б) на положительном Hg2SO4 + 2e = 2Hg + SO42-. Cуммарная реакция, протекающая в гальваническом элементе: Сd + Hg2SO4 = Cd2+ + 2Hg + SO42-. Как видно, эта реакция идентична изучаемой. Значение DG° находим по формуле (3.56), учитывая, что z = 2 (число электронов, принимающих участие в реакциях) и Т=298 К: DG° = – 2×96485×(1,0183 – 3,8×10-5×5 – 6,5.10-7×52) = – 196497,5 Дж. DG° = – 196,5 кДж. Отрицательное значение энергии Гиббса указывает на то, что, при постоянном давлении и температуре, при работе нормального элемента Вестона процесс протекает самопроизвольно. Для вычисления энергии Гельмгольца DА° используем выражение (3.57). Поскольку в электрохимической реакции, протекающей в элементе, газообразные вещества не участвуют, то Dn=0. Следовательно, DA° = DG° = – 196,5 кДж. Чтобы оценить значения DS° и DH°, необходимо определить температурный коэффициент ЭДС электрохимического элемента. Для этого продифференцируем по температуре уравнение зависимости Е от Т:
Таким образом, значение температурного коэффициента ЭДС при 298 К равно:
Изменение энтропии в ходе реакции определяем по формуле (3.59)
Тепловой эффект данной химической реакции с учетом формулы (3.62) равен:
Полученный результат показывает, что реакция в электрохимическом элементе протекает с выделением тепла. Изменение внутренней энергии определяется по формуле (3.61). Поскольку среди компонентов электрохимической реакции, протекающей в элементе, нет газообразных веществ (Dn=0), следовательно
Пример 2. Гальванический элемент (–) Hg, Hg2Cl2 ½ KCl aq. ║ MnO использован для определения рН раствора. Если активность ионов MnO Решение. Запишемэлектродную реакцию и потенциал положительного электрода: MnO
ЭДС элемента равна разности потенциалов положительного и отрицательного электродов:
Откуда рН раствора равно:
Пример 3. ЭДС элемента при 298 К равна 0,72 В. Средний коэффициент активности KI в 1 М растворе равен 0,65, а средний коэффициент активности AgNO3 в 0,001 М растворе равен 0,98. Каково произведение растворимости соли AgI? Какова растворимость соли AgI в чистой воде? Решение. Составляем гальванический элемент (–) Ag, AgI½KI aq. ║ AgNO3 aq. ½ Ag (+) c' = 1 M; c"=0,001 M. Этот элемент можно рассматривать как концентрационный по отношению к ионам серебра в каждом из растворов. По ЭДС этого элемента можно вычислить произведение растворимости малорастворимой соли:
где
тогда:
Откуда Lp = 4,03.10-16. Растворимость соли AgI определяется концентрацией ионов серебра при растворении данной соли в дистиллированной воде и рассчитывается по соотношению:
Пример 4. Рассчитать средний коэффициент активности электролита ZnCl2, ели стандартная ЭДС элемента Znç ZnCl2aqçAgCl,Ag равна 0,982 В. ЭДС этого элемента при изменении концентрации электролита ZnCl2 изменялась следующим образом:
Решение. В рассматриваемом элементе отрицательный электрод (цинковый) обратим относительно катиона, а положительный (хлорсеребрянный) – обратим относительно аниона. ЭДС элемента, составленного из электрода первого рода и электрода второго рода, равна:
Используя понятие средней активности ионов электролита, объединим под один логарифм активности ионов ZnCl2:
Откуда:
Значение логарифма среднего коэффициента активности ионов ZnCl2 равно:
Значения средних коэффициентов активности ионов ZnCl2 при разных концентрациях электролита равны:
Как видно из полученных данных, с ростом концентрации электролита средний коэффициент активности уменьшается.
Вопросы для самоконтроля 1. Перечислите правила схематической записи электрохимических цепей. Приведите примеры. 2. Что представляет собой стандартный электродный потенциал электрохимического процесса? Как экспериментально можно определить его значение? 3. В чем заключается порядок выполнения работы? 4. Выразите значение произведения растворимости исследуемой соли от потенциала используемой электрохимической цепи и активностей потенциалопределяющих веществ. 5. Как определить произведение растворимости исследуемой соли графическим методом? В каких координатах должна наблюдаться линейная зависимость? 6.Как можно учесть неидеальность раствора при переходе от концентрации иона к его активности. Как определяется ионная сила раствора. Как необходимо изменить координаты графика, чтобы учесть изменение ионной силы растворов? 7. Предложите электрохимический элемент и порядок выполнения работы для определения константы устойчивости комплекса [Ag(S2O3)2]3–.
|
|||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-10; просмотров: 1762; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.146.255.211 (0.012 с.) |

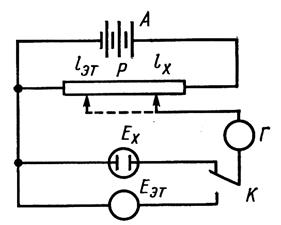 Рис. 5. Схема измерения ЭДС гальванического элемента компенсационным методом. А – аккумулятор; Р – потенциометр; К – переключатель; Е – эталонный гальванический элемент (элемент Вестона); Ех– элемент с неизвестной ЭДС.
Рис. 5. Схема измерения ЭДС гальванического элемента компенсационным методом. А – аккумулятор; Р – потенциометр; К – переключатель; Е – эталонный гальванический элемент (элемент Вестона); Ех– элемент с неизвестной ЭДС.
 . (3.47)
. (3.47) . (3.48)
. (3.48)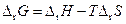 . (3.49)
. (3.49)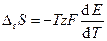 . (3.50)
. (3.50) A+ + B–
A+ + B–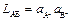 . (3.51)
. (3.51) , (3.52)
, (3.52) . (3.53)
. (3.53) . (3.54)
. (3.54) . (3.55)
. (3.55) (DG, DA, DS, DH и DU). Для этого необходимо составить электрохимический элемент, результатом работы которого была бы исследуемая химическая реакция. По ЭДС этого гальванического элемента можно рассчитать:
(DG, DA, DS, DH и DU). Для этого необходимо составить электрохимический элемент, результатом работы которого была бы исследуемая химическая реакция. По ЭДС этого гальванического элемента можно рассчитать: (3.58)
(3.58) – температурный коэффициент ЭДС. Величину температурного коэффициента ЭДС определяют экспериментально по графической или аналитической зависимости ЭДС элемента от температуры.
– температурный коэффициент ЭДС. Величину температурного коэффициента ЭДС определяют экспериментально по графической или аналитической зависимости ЭДС элемента от температуры. (3.59)
(3.59) ) - Dn ×RT. (3.60)
) - Dn ×RT. (3.60) ). (3.61)
). (3.61)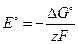 , (3.63)
, (3.63) , (3.64)
, (3.64) . (3.65)
. (3.65) .
.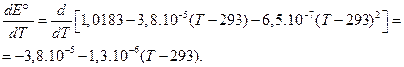
 В/К.
В/К. Дж/К.
Дж/К. Дж;
Дж;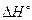 = –199,06 кДж.
= –199,06 кДж. кДж.
кДж. , Mn2+, H+ ½ Pt (+);
, Mn2+, H+ ½ Pt (+); ;
;
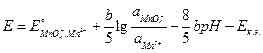
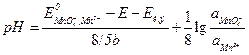 ;
;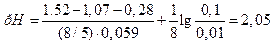 .
. ,
, ;
; ,
, .
. M.
M. .
. ;
;  .
. .
. .
.


