
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Электрохимический потенциал и равновесие на границе электрод/раствор. Условный электродный потенциал. Уравнение НернстаСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
В химической термодинамике для характеристики свойств систем, не содержащих заряженные частицы, и в которых изменение состава происходит в результате протекания химических реакций или фазовых превращений используют фундаментальное уравнение Гиббса, выраженное через характеристическую функцию
где При рассмотрении явлений в гетерогенных системах, необходимо учитывать к какой фазе относятся величины Если компонент
где - Внутренним потенциалом Термин «воображаемый» предполагает, что этот единичный заряд реагирует только на внешнее электрическое поле и не взаимодействует со средой. Так как
Все производные энергии Гиббса по обобщенным координатам имеют смысл обобщенных сил. Поэтому
При перемещении одного моля реальных заряженных частиц Фундаментальное уравнение Гиббса тогда запишется:
Рассмотрим равновесие на границе раздела фаз. Предположим, что на границе раздела фаз протекает электрохимическая реакция (электродная реакция)
где При протекании химической реакции количества отдельных реагентов изменяются пропорционально их стехиометрическим коэффициентам в уравнении реакции. Взаимную пропорциональность величин d ni можно выразить совокупностью уравнений:
Таким образом, перераспределение количеств всех веществ в системе можно выразить с помощью единственной переменной, которая обозначается x и называется химической переменной. Дифференциал химической переменной определяется с помощью любого из приведенных выше уравнений:
d ni = nI d x; Тогда с учетом этого выражения для d G получим d G = – S d T + V d p + При постоянной температуре и постоянном давлении условием равновесия в системе является минимум энергии Гиббса. Это означает, что для равновесной системы
В этом уравнении суммируются электрохимические потенциалы и стехиометрические коэффициенты всех участников электрохимической реакции, независимо от того, в какой фазе они находятся. Равновесие на электроде характеризуется равенством электрохимических потенциалов компонентов во всех фазах. В случае их неравенства происходит переход заряженных частиц через границу раздела фаз, что вызывается стремлением системы к термодинамическому равновесию. В результате этого нарушается баланс электрических зарядов в каждой фазе, металл и раствор приобретают электрический заряд и на границе их раздела возникает скачок потенциала. Другими словами между фазами электрода возникает определенная разность потенциалов, обусловленная природой составляющих электрод компонентов, их концентрациями и значениями внешних термодинамических параметров. Этот скачек потенциала называется гальвани-потенциалом (потенциалом электрода) и обозначается
Рис. Возникновение скачка потенциала (гальвани-потенциала Рассмотрим механизм возникновения скачка потенциала на примере наиболее часто встречающихся электродов с границей раздела фаз металл – раствор. Существуют такие металлы, что если их опустить в воду или в раствор, то ионы металла переходят в прилегающий к поверхности металла слой воды или раствора по реакции Этот переход происходит в том случае, если электрохимический потенциал иона металла в кристалле больше чем электрохимический потенциал сольватированного иона в растворе. Металл можно представить состоящим из положительно заряженных ионов металла и относительно свободных электронов. По мере перехода ионов в раствор, состояние системы постепенно изменяется. Металл приобретает отрицательный заряд, величина которого увеличивается по мере протекания электрохимической реакции. В связи с этим электрохимический потенциал ионов металла на поверхности уменьшается. Количество ионов в растворе возрастает, и их электрохимический потенциал увеличивается вследствие отталкивания одноименных ионов. В результате этого скорость перехода ионов в раствор уменьшается, а скорость обратного процесса – перехода ионов из раствора на металл возрастает. Наконец наступает такое состояние, при котором скорости обоих процессов становятся одинаковыми, то есть в системе наступает равновесие. При этом металл приобретает отрицательный заряд, которому соответствует определенный потенциал, а в растворе образуется избыток катионов, которые удерживаются у поверхности металлического электрода в результате действия электростатических сил и этому слою соответствует свой потенциал. Эти потенциалы называются внутренними потенциалами и обозначаются (например, Для определения величины гальвани-потенциала, возникающего на границе раздела фаз
Из уравнения следует, что измерение гальвани-потенциала между точками в разных фазах возможно лишь при условии равенства химических потенциалов веществ в разных фазах, то есть при
Отсюда следует, что на границе раздела двух фаз различного состава экспериментально определить гальвани-потенциал невозможно. Величина гальвани-потенциала зависит от свойств фаз, образующих границу раздела и от концентрации ионов в растворе. В общем случае, для электрохимической реакции
протекающей на границе раздела фаз, условие равновесия, в соответствие с (3.6) запишется:
где
В соответствии с балансом зарядов где
Так как стандартный химический потенциал компонента равен значению его стандартной энергии Гиббса, получим
Тогда,
Объединив все постоянные величины в одну величину — j °, которая называется стандартным электродным потенциалом, получим выражение для разности потенциалов между фазами, составляющими электрод:
где j ° - стандартный электродный потенциал; R – универсальная газовая постоянная; T –температура, К; F – постоянная Фарадея; Полученное уравнение называется уравнением Нернста. Стандартный электродный потенциал j ° — это величина, характерная для каждого электродного процесса, которая также зависит от температуры и природы растворителя. Стандартный электродный потенциал равен потенциалу электрода в котором отношение активностей всех участников электродной реакции равны единице. Уравнение Нернста связывает величину разности потенциалов между фазой раствора электролита и фазой проводника первого рода с активностями компонентов, участвующих в электродной реакции. В качестве примера установления электрохимического равновесия рассмотрим наиболее простой случай – равновесие на границе металла с раствором, содержащим ионы этого металла. На электроде будет протекать следующая электрохимическая реакция:
Равновесие устанавливается в результате перехода ионов металла из объема раствора на металл и обратно при условии выполнения равенства (3.6). Тогда условие равновесия для данной системы запишется:
Из уравнения следует, что равновесный гальвани-потенциал на границе металл–раствор равен:
Для нейтральных атомов металла электрохимический потенциал равен химическому потенциалу -
где С учетом вышесказанного уравнение (3.11) будет иметь следующий вид:
Объединив все постоянные величины в одну величину — j °, которая называется стандартным электродным потенциалом, получим выражение для разности потенциалов между фазами, составляющими электрод:
Комбинация констант R, F и температуры (RT / F) часто встречается в электрохимических уравнениях; она имеет размерность напряжения. Общепринято обозначать ее как b0. Часто уравнение Нернста записывается через десятичные логарифмы. Переход к десятичным логарифмам осуществляется путем умножения b0 на ln10 = 2,3 (это произведение обозначается как b). При 298 К значения b0 и b соответственно равны:
Значения постоянной b при других температурах могут быть легко рассчитаны. Следует отметить, что в общем случае при записи уравнения Нернста под логарифмом остаются только те величины, которые могут варьироваться. Таким образом, при записи уравнения Нернста для разных случаев необходимо соблюдать несколько правил, связанных с применением выражения (3.9) для различных типов электродов: 1. Активности чистых компонентов, образующих отдельную фазу постоянного состава, (как правило, это твердые вещества) принимаются равными единице. 2. Активность растворителя принимается равной единице. 3. Вместо активностей газообразных веществ в уравнение входят относительные парциальные давления этих газов над раствором
Использование парциальных давлений справедливо для случая не очень высоких давлений (порядка нескольких бар). В случае высоких давлений необходимо использовать фугитивности газов.
|
||||
|
Последнее изменение этой страницы: 2016-12-10; просмотров: 425; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.119.158.110 (0.007 с.) |

 :
: , (3.1)
, (3.1) - химический потенциал
- химический потенциал  -го реагента, а
-го реагента, а  - бесконечно малое изменение количества этого реагента.
- бесконечно малое изменение количества этого реагента. ,
,  ,
,  . Принадлежность к определенной фазе указывается верхним индексом, например -
. Принадлежность к определенной фазе указывается верхним индексом, например -  ,
, 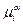 . Условием равновесия в гетерофазной системе при постоянных температуре и давлении (Т и Р – const) является равенство химических потенциалов
. Условием равновесия в гетерофазной системе при постоянных температуре и давлении (Т и Р – const) является равенство химических потенциалов  , где
, где 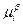 - химические потенциалы нейтрального вещества в двух сосуществующих фазах.
- химические потенциалы нейтрального вещества в двух сосуществующих фазах. . Фундаментальное уравнение Гиббса в этом случае должно иметь вид:
. Фундаментальное уравнение Гиббса в этом случае должно иметь вид: , (3.2)
, (3.2) - внутренний потенциал какой либо фазы, то есть внутренний потенциал той части системы, в которой находится данная частица.
- внутренний потенциал какой либо фазы, то есть внутренний потенциал той части системы, в которой находится данная частица. называется работа переноса единичного отрицательного воображаемого заряда из бесконечно удаленной точки А, находящейся в вакууме, в точку В, находящуюся внутри проводящей фазы
называется работа переноса единичного отрицательного воображаемого заряда из бесконечно удаленной точки А, находящейся в вакууме, в точку В, находящуюся внутри проводящей фазы 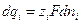 , где
, где 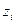 - заряд
- заряд  - постоянная Фарадея,
- постоянная Фарадея, 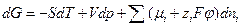 . (3.3)
. (3.3) - это обобщенная сила в явлениях переноса заряженных частиц в электрическом поле. По аналогии с химическим потенциалом, для электрохимических систем, величина
- это обобщенная сила в явлениях переноса заряженных частиц в электрическом поле. По аналогии с химическим потенциалом, для электрохимических систем, величина ) из бесконечности в вакууме вглубь проводящей фазы (например, фазы
) из бесконечности в вакууме вглубь проводящей фазы (например, фазы 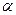 ), затраченная работа состоит из двух частей: электростатической равной
), затраченная работа состоит из двух частей: электростатической равной  и химической, обусловленной взаимодействием реальных частиц с данной фазой, то есть химическим потенциалом
и химической, обусловленной взаимодействием реальных частиц с данной фазой, то есть химическим потенциалом  . (3.4)
. (3.4) (1)
(1) и
и  — стехиометрический коэффициент i -го вещества или иона (для исходных веществ стехиометрические коэффициенты принимают отрицательные значения, а для продуктов реакции — положительные), z — общее число электронов участвующих в электродной реакции (полуреакции).
— стехиометрический коэффициент i -го вещества или иона (для исходных веществ стехиометрические коэффициенты принимают отрицательные значения, а для продуктов реакции — положительные), z — общее число электронов участвующих в электродной реакции (полуреакции).
 ;
;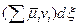 . (3.5)
. (3.5) ;
;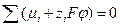 . (3.6)
. (3.6) . Гальвани-потенциал определяется разностью внутренних потенциалов обеих фаз:
. Гальвани-потенциал определяется разностью внутренних потенциалов обеих фаз:  .
.
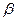 .
. .
. ).
). , то
, то . (3.7)
. (3.7) . (3.8)
. (3.8) ,
, и
и  - заряды частиц окисленной и восстановленной форм,
- заряды частиц окисленной и восстановленной форм,  и
и 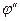 - потенциалы фаз, содержащих окисленную и восстановленную формы вещества. После преобразования уравнения получим:
- потенциалы фаз, содержащих окисленную и восстановленную формы вещества. После преобразования уравнения получим: .
. ,
, - суммарный заряд ионов, участвующих в реакции в фазе, содержащей восстановленную форму вещества, а
- суммарный заряд ионов, участвующих в реакции в фазе, содержащей восстановленную форму вещества, а  - суммарный заряд ионов, участвующих в реакции в фазе, содержащей окисленную форму вещества. Для произвольных жидких и твердых растворов химический потенциал i -го компонента выражается через его активность уравнением
- суммарный заряд ионов, участвующих в реакции в фазе, содержащей окисленную форму вещества. Для произвольных жидких и твердых растворов химический потенциал i -го компонента выражается через его активность уравнением  . Учитывая, что
. Учитывая, что  - гальвани-потенциал, получаем:
- гальвани-потенциал, получаем: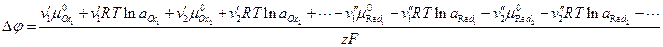
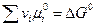 .
. .
. . (3.9)
. (3.9) - число электронов, участвующих в электродном процессе;
- число электронов, участвующих в электродном процессе;  и
и  - активность окисленной и восстановленной форм.
- активность окисленной и восстановленной форм. .
. , или
, или  . (3.10)
. (3.10) . (3.11)
. (3.11) , а химический потенциал ионов выражается через активность ионов в растворе (ai) уравнением
, а химический потенциал ионов выражается через активность ионов в растворе (ai) уравнением - стандартный химический потенциал i –го реагента, R — универсальная газовая постоянная, равная 8,314 Дж/(моль К), T — температура, К.
- стандартный химический потенциал i –го реагента, R — универсальная газовая постоянная, равная 8,314 Дж/(моль К), T — температура, К. . (3.13)
. (3.13) . (3.14)
. (3.14) ;
;  . (3.15)
. (3.15)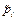 . Давление приводится относительно стандартного (1 бар = 105 Па), т. о. эта величина является безразмерной, хотя численно она совпадает с парциальным давлением газа, выраженным в барах.
. Давление приводится относительно стандартного (1 бар = 105 Па), т. о. эта величина является безразмерной, хотя численно она совпадает с парциальным давлением газа, выраженным в барах. . (3.16)
. (3.16)


