
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Зависимость константы скорости реакции от температурыСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Скорость большинства химических реакций возрастает при повышении температуры. Так как концентрация реагирующих веществ, практически не зависит от температуры, то в соответствии с кинетическим уравнением реакции Зависимость скорости реакции от температуры можно характеризовать величиной температурного коэффициента Экспериментальные данные по влиянию температуры на скорость многих химических реакций при обычных температурах (273–373 К), в небольшом интервале температур показали, что повышение температуры на 10 градусов увеличивает скорость реакции в 2-4 раза (правило Вант-Гоффа). По Вант-Гоффу- температурный коэффициент константы скорости (коэффициент Вант-Гоффа) – это возрастание скорости реакции при увеличении температуры на 10 градусов.
где При повышении температуры на n десятков градусов отношение констант скоростей будет равно
где n может быть как целым, так и дробным числом. Правило Вант-Гоффа это приближенное правило. Оно применимо в узком интервале температур, так как температурный коэффициент изменяется с температурой. Более точная зависимость константы скорости реакции от температуры выражается полуэмпирическим уравнением Аррениуса
где А - предэкспоненциальный множитель который не зависит от температуры, а определяется только видом реакции; Е – энергия активации химической реакции. Энергию активации можно представить как некоторую пороговую энергию, характеризующую высоту энергетического барьера на пути реакции. Энергия активации также не зависит от температуры. Эта зависимость установлена в конце XIX в. голландским ученым Аррениусом для элементарных химических реакций. Энергия активации прямой (Е 1) и обратной (Е 2) реакции связана с тепловым эффектом реакции D Н соотношением (см. рис 1): Е 1 – Е 2 = D Н. Если реакция эндотермическая и D Н> 0, то Е 1 > Е 2 и энергия активации прямой реакции больше обратной. Если реакция экзотермическая, то Е 1 < Е 2. Уравнение Аррениуса (101) в дифференциальной форме можно записать:
Из уравнения следует, что чем больше энергия активации Е, тем быстрее растет скорость реакции с температурой. Разделив переменные k и T и, считая E постоянной величиной, после интегрирования уравнения (4.66) получим:
Рис. 5. График ln k – 1/T.
где А – предэкспоненциальный множитель, имеющий размерность константы скорости. Если это уравнение справедливо, то на графике в координатах Энергию активации химической реакции можно вычислить по значениям констант скоростей при двух различных температурах по уравнению
Теоретический вывод уравнения Аррениуса сделан для элементарных реакций. Но опыт показывает, что подавляющее большинство сложных реакций также подчиняются этому уравнению. Однако для сложных реакций энергия активации и предэкспоненциальный множитель в уравнении Аррениуса не имеют определенного физического смысла. Уравнение Аррениуса (4.67) позволяет дать удовлетворительное описание большого круга реакций в узком температурном интервале. Для описания зависимости скорости реакции от температуры применяют также модифицированное уравнение Аррениуса
в которое входят уже три параметра: А, Е и n. Уравнение (4.69) широко используется для реакций, протекающих в растворах. Для некоторых реакций зависимость константы скорости реакции от температуры отличается от приведенных выше зависимостей. Так, например, в реакциях третьего порядка константа скорости убывает с увеличением температуры. В цепных экзотермических реакциях константа скорости реакции резко возрастает при температуре выше некоторого предела (тепловой взрыв). 4.5.1. Примеры решения задач Пример 1. Константа скорости некоторой реакции с увеличением температуры изменялась следующим образом: t 1 = 20°С; k 1 = 2,76 10-4 мин.-1; t 2 = 50 0С; k 2= 137,4 10-4 мин.-1 Определить температурный коэффициент константы скорости химической реакции. Решение. Правило Вант –Гоффа позволяет рассчитать температурный коэффициент константы скорости по соотношению g n = g3 = Пример 2. С помощью правила Вант-Гоффа вычислить, при какой температуре реакция закончится за 15 мин., если при температуре 20 0С потребовалось 120 мин. Температурный коэффициент скорости реакции равен 3. Решение. Очевидно, чем меньше время протекания реакции (t), тем больше константа скорости реакции:
3 n = 8, n ln3 = ln8, n= Температура, при которой реакция закончится за 15 минут, равна: 20 + 1,9×10 = 39 0С. Пример 3. Константа скорости реакции омыления уксусно-этилового эфира раствором щелочи при температуре 282,4 К равна2,37л2/моль2мин., а при температуре 287,40 К равна 3,2л2/моль2мин. Найти, при какой температуре константа скорости данной реакции равна 4? Решение. 1. Зная значения констант скоростей при двух температурах, можно найти энергию активации реакции:
2. Зная значение энергии активации, из уравнения Аррениуса
можно рассчитать Т 3 – температуру, при которой k 3 = 4.
Вопросы и задания для самоконтроля. 1.Какие величины называются «аррениусовскими» параметрами? 2.Какой минимум опытных данных необходим для расчета энергии активации химической реакции? 3. Покажите, что температурный коэффициент константы скорости зависит от температуры. 4. Существуют ли отклонения от уравнения Аррениуса? Как можно описать зависимость константы скорости от температуры в этом случае?
Кинетика сложных реакций Реакции, как правило, не протекают путем непосредственного взаимодействия всех исходных частиц с прямым переходом их в продукты реакции, а состоят из нескольких элементарных стадий. Это, прежде всего, относится к реакциям, в которых, согласно их стехиометрическому уравнению, принимает участие более трех частиц. Однако, даже реакции двух или одной частицы часто идут не по простому би- или мономолекулярному механизму, а более сложным путем, то есть через ряд элементарных стадий. Реакции называются сложными, если расходование исходных веществ и образование продуктов реакции происходит через ряд элементарных стадий, которые могут протекать одновременно или последовательно. При этом некоторые стадии проходят с участием веществ, не являющихся ни исходными веществами, ни продуктами реакции (промежуточные вещества). В качестве примера сложной реакции можно рассмотреть реакцию хлорирования этилена с образованием дихлорэтана. Прямое взаимодействие В результате этих двух стадий одна молекула
При всем многообразии, сложные реакции можно свести к комбинации нескольких типов сложных реакций, а именно параллельных, последовательных и последовательно-параллельных реакций. Две стадии называются последовательными, если частица, образующаяся в одной стадии, является исходной частицей в другой стадии. Например, в приведенной схеме последовательными являются первая и вторая стадии:
Две стадии называются параллельными, если в обеих в качестве исходной принимают участие одни и те же частицы. Например, в схеме реакции параллельными являются четвертая и пятая стадии:
Две стадии называются последовательно-параллельными, если они являются параллельными по отношению к одной и последовательными по отношению к другой из участвующих в этих стадиях частиц. Примером последовательно-параллельных стадий являются вторая и четвертая стадии данной схемы реакции. К характерным признакам того, что реакция протекает по сложному механизму, относятся следующие признаки: - несовпадение порядка реакции и стехиометрических коэффициентов; - изменение состава продуктов в зависимости от температуры, начальных концентраций и других условий; - ускорение или замедление процесса при добавлении в реакционную смесь небольших количеств веществ; - влияние материала и размеров сосуда на скорость реакции и др. При кинетическом анализе сложных реакций применяют принцип независимости: «Если в системе протекают одновременно несколько простых реакций, то основной постулат химической кинетики применяется к каждой из них, как если бы данная реакция была единственной». Этот принцип можно сформулировать и следующим образом: «Величина константы скорости элементарной реакции не зависит от того, протекают ли в данной системе одновременно другие элементарные реакции». Принцип независимости справедлив для большинства реакций, протекающих по сложному механизму, но не является всеобщим, та как существуют реакции, в которых одни простые реакции влияют на протекание других (например, сопряженные реакции.) Важное значение при изучении сложных химических реакций имеет принцип микрообратимости или детального равновесия: если в сложном процессе устанавливается химическое равновесие, то скорости прямой и обратной реакции должны быть равны для каждой из элементарных стадий. Наиболее распространенным случаем протекания сложной реакции будет случай, когда реакция идет через несколько простых стадий, протекающих с разными скоростями. Различие в скоростях приводит к тому, что кинетика получения продукта реакции может определяться закономерностями только одной реакции. Например, для параллельных реакций скорость всего процесса определяется скоростью наиболее быстрой стадии, а для последовательных – наиболее медленной. Следовательно, при анализе кинетики параллельных реакций при значительной разнице в константах можно пренебречь скоростью медленной стадии, а при анализе последовательных реакций – не обязательно определять скорость быстрой реакции. В последовательных реакциях наиболее медленная реакция называется лимитирующей. У лимитирующей стадии самая маленькая константа скорости. Если значения констант скоростей отдельных стадий сложной реакции близки, то необходим полный анализ всей кинетической схемы. Введение понятия стадии, определяющей скорость, во многих случаях упрощает математическую сторону рассмотрения подобных систем и объясняет тот факт, что иногда кинетика сложных, многостадийных реакций хорошо описывается простыми уравнениями, например первого порядка.
|
||||
|
Последнее изменение этой страницы: 2016-12-10; просмотров: 914; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.22.68.228 (0.007 с.) |

 основное влияние температуры на скорость реакции осуществляется через изменение константы скорости реакции. При увеличении температуры возрастает энергия сталкивающихся частиц и повышается вероятность того, что при столкновении произойдет химическое превращение.
основное влияние температуры на скорость реакции осуществляется через изменение константы скорости реакции. При увеличении температуры возрастает энергия сталкивающихся частиц и повышается вероятность того, что при столкновении произойдет химическое превращение. .
. (4.63)
(4.63) и
и  — константы скорости при температурах
— константы скорости при температурах  и
и 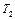 ;
; 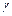 — температурный коэффициент скорости реакции.
— температурный коэффициент скорости реакции. , (4.64)
, (4.64) (4.65)
(4.65) . (4.66)
. (4.66)
 , (4.67)
, (4.67) опытные точки располагаются на прямой линии под углом a к оси абсцисс и угловой коэффициент (
опытные точки располагаются на прямой линии под углом a к оси абсцисс и угловой коэффициент ( ) равен
) равен  , что позволяет рассчитать энергию активации химической реакции по зависимости константы скорости от температуры по уравнению
, что позволяет рассчитать энергию активации химической реакции по зависимости константы скорости от температуры по уравнению  .
.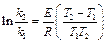 . (4.68)
. (4.68) , (4.69)
, (4.69) =2 ¸ 4, где n =
=2 ¸ 4, где n =  =
= 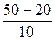 =3;
=3; =49,78 g = 3,68
=49,78 g = 3,68 =
=  =
=  =
=  ;
;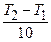 =
=  .
. =
=  = 40,8 кДж/моль.
= 40,8 кДж/моль. ,
,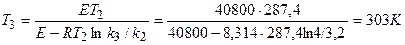 .
. и
и  должно идти через четырехчленный активированный комплекс, что сопряжено с преодолением высокого энергетического барьера. Скорость такого процесса мала. Если же в системе тем или иным путем (например, при действии света) образуются атомы
должно идти через четырехчленный активированный комплекс, что сопряжено с преодолением высокого энергетического барьера. Скорость такого процесса мала. Если же в системе тем или иным путем (например, при действии света) образуются атомы  , то процесс может пойти по цепному механизму. Атом
, то процесс может пойти по цепному механизму. Атом  . Этот свободный радикал может легко оторвать атом
. Этот свободный радикал может легко оторвать атом  от молекулы
от молекулы  с образованием конечного продукта -
с образованием конечного продукта -  , в результате чего регенерируется свободный атом
, в результате чего регенерируется свободный атом 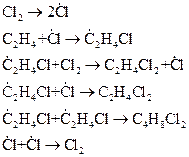

 .
. ;
;  .
.


