
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Кинетика параллельных химических реакцийСодержание книги
Поиск на нашем сайте
1. Рассмотрим две параллельные реакции, протекающие, например, при разложении вещества А с образованием веществ В и Д
Обе стадии процесса протекают как реакции первого порядка. Согласно основному постулату химической кинетики скорость реакции или скорость превращения вещества А равна сумме скоростей по обоим направлениям.
или
где Разделив переменные, получим:
Интегрируя это уравнение в пределах от 0 до t и от х =0 до х, получим:
Полученное уравнение имеет тот же вид, что и уравнение для необратимой реакции первого порядка. Из этого уравнения следует, что
Скорости образования веществ В и Д равны:
Подставляя в полученные уравнения выражение (4.90) для
Интегрирование этих уравнений в пределах от 0 до t и, соответственно, от 0 до
Выражение для Интегральной селективностью процесса при наличии параллельных реакций называется отношение концентрации основного продукта к сумме концентраций всех продуктов, полученных в результате реакции. Если считать вещество В основным (полезным) продуктом, а вещество Д побочным, то можно найти интегральную селективность реакции относительно вещества В (sВ) sВ
Из уравнений (4.96 и 4.97) видно, что экспериментальным критерием того, что реакция протекает по механизму параллельных процессов, является то, что отношение концентраций продуктов реакции есть величина постоянная в любой момент времени протекания процесса:
Отсюда значение интегральной селективности реакции равно: s =
Как видно из уравнения (4.100), селективность параллельно протекающих реакций остается постоянной в течение всего процесса. При решении обратной кинетической задачи, значение 2.Рассмотрим случай, когда параллельные реакции являются реакциями второго порядка. Такой процесс можно представить общей схемой:
Кинетическое уравнение в дифференциальной форме можно представить как:
Интегрирование этого уравнения позволяет оценить сумму констант скоростей:
Отношение концентраций продуктов, как и в первом случае, не зависит от времени и определяется отношением констант скоростей
Следует отметить, что часто встречаются параллельные реакции второго порядка и параллельные, двусторонние реакции, как первого, так и второго порядка. Для математического описания кинетики таких реакций, используя основные положения формальной кинетики, составляют систему дифференциальных уравнений, характеризующих скорости образования отдельных реагентов. Решение таких систем дифференциальных уравнений осуществляется численными методами с использованием ЭВМ.
|
||||
|
Последнее изменение этой страницы: 2016-12-10; просмотров: 345; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.129.42.59 (0.005 с.) |


 , (4.86)
, (4.86) (4.87)
(4.87)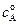 - начальная концентрация вещества А, х – изменение концентрации вещества А или общая концентрация продуктов реакции (при
- начальная концентрация вещества А, х – изменение концентрации вещества А или общая концентрация продуктов реакции (при  ).
). (4.88)
(4.88) . (4.89)
. (4.89) (4.90)
(4.90) . (4.91)
. (4.91) ; (4.92)
; (4.92) (4.93)
(4.93) и разделив переменные получим:
и разделив переменные получим: (4.94)
(4.94) (4.95)
(4.95) и
и  дает:
дает: ; (4.96)
; (4.96) . (4.97)
. (4.97) ):
):  . Отсюда
. Отсюда  . Подставляя в это уравнение выражение для
. Подставляя в это уравнение выражение для  и
и  . (4.98)
. (4.98) . (4.99)
. (4.99) . (4.100)
. (4.100)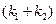 можно определить по тангенсу угла наклона графической зависимости
можно определить по тангенсу угла наклона графической зависимости  . Так как
. Так как  то, зная (
то, зная ( ) и концентрации
) и концентрации 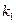 и
и  из уравнений (4.96) и (4.97).
из уравнений (4.96) и (4.97).
 . (4.101)
. (4.101) . (4.102)
. (4.102) . (4.103)
. (4.103)


