
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Кинетика двусторонних (обратимых) химических реакцийСодержание книги
Поиск на нашем сайте
1. Рассмотрим двустороннюю (обратимую) реакцию
протекающую в закрытой системе при постоянном объеме, когда обе стадии, прямая и обратная, являются реакциями первого порядка. Если скорости прямой и обратной реакций в изучаемом диапазоне условий соизмеримы, то, согласно закону действующих масс, выражение для суммарной скорости записывается в виде разности скоростей прямой и обратной реакций.
откуда
Пусть начальные концентрации веществ А и В равны соответственно
Преобразуя уравнение (4.71), получим:
В момент равновесия (
где Kс –константа равновесия реакции. Решив уравнение (4.73) относительно
Подставив (4.74) в (4.72) получим:
Разделяя переменные и интегрируя от
Уравнение (4.77) аналогично уравнению (4.24) для односторонней реакции первого порядка, с той лишь разницей, что вместо Количество вещества, вступившего в реакцию к моменту времени t можно рассчитать, по соотношению:
Изменение концентрации реагентов и продуктов реакции во времени можно изобразить на графике (рис 6).
Рис. 6 Зависимость концентрации реагентов от времени Для обратимой реакции первого порядка.1 – продукт реакции, 2 –исходное вещество. Выражение (4.78)можно также представить в виде уравнения прямой линии:
Таким образом, для обратимой реакции первого порядка должна соблюдаться линейная зависимость функции Для расчета значений каждой из констант, необходимо рассчитать константу равновесия реакции
Зная значения
2. Типичным примером обратимой химической реакции, в которой обе реакции протекают как реакции второго порядка, является реакция омыления сложного эфира
Схема такой реакции
Решение задачи рассмотрим для случая, когда продукты реакции до начала реакции в реакционной смеси отсутствуют: СА0= СВ0= а. Уравнение скорости химической реакции можно записать в виде:
При достижении состояния равновесия выполняется условие:
С учетом уравнения (4.81) уравнение (4.80) для скорости химической реакции запишется как:
Полином допускает наличие двух корней квадратного уравнения х 1= х ∞ и х 2=
Интегральная форма этого уравнения имеет вид
Константы скоростей k 1 и k 2можно определить из опытного значения кажущейся константы скорости:
|
||
|
Последнее изменение этой страницы: 2016-12-10; просмотров: 437; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.108 (0.007 с.) |

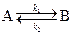 ,
,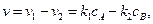 (4.69)
(4.69)
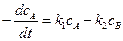 . (4.70)
. (4.70)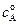 и
и  , а количество прореагировавшего вещества А в единице объема, то есть уменьшение концентрации вещества А к моменту времени t равно х. Из условия материального баланса можно записать
, а количество прореагировавшего вещества А в единице объема, то есть уменьшение концентрации вещества А к моменту времени t равно х. Из условия материального баланса можно записать  и
и  . После введения этих обозначений, уравнение (4.70) можно записать в следующем виде:
. После введения этих обозначений, уравнение (4.70) можно записать в следующем виде: (4.71)
(4.71) . (4.72)
. (4.72) ) скорость двусторонней реакции будет равна нулю, то есть
) скорость двусторонней реакции будет равна нулю, то есть 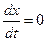 и
и 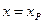 , где
, где  - количество вещества А в единице объема, прореагировавшего к моменту установления равновесия. Тогда
- количество вещества А в единице объема, прореагировавшего к моменту установления равновесия. Тогда  , откуда
, откуда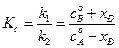 , (4.73)
, (4.73) получим соотношение:
получим соотношение: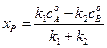 . (4.74)
. (4.74) (4.75)
(4.75) до
до  и от
и от  до
до  получим:
получим: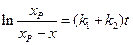 и (4.76)
и (4.76)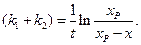 (4.77)
(4.77)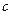 , в нем фигурируют соответственно
, в нем фигурируют соответственно 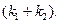
 . (4.78)
. (4.78)
 (4.78)
(4.78)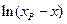 от времени. Из значения тангенса угла наклона прямой можно вычислить сумму констант скоростей прямой и обратной реакций –
от времени. Из значения тангенса угла наклона прямой можно вычислить сумму констант скоростей прямой и обратной реакций – 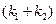 .
. из термодинамических (можно справочных) данных или по формуле (4.73):
из термодинамических (можно справочных) данных или по формуле (4.73): , нетрудно рассчитать каждую из констант отдельно:
, нетрудно рассчитать каждую из констант отдельно: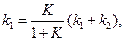
 . (4.79)
. (4.79)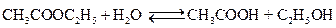

 . (4.80)
. (4.80) . (4.81)
. (4.81)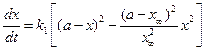 . (4.82)
. (4.82) , его записывают через произведение вида: m (х - х 1) (х - х 2). Уравнение скорости химической реакции запишется как:
, его записывают через произведение вида: m (х - х 1) (х - х 2). Уравнение скорости химической реакции запишется как: . (4.83)
. (4.83)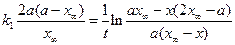 . (4.84)
. (4.84)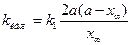 и
и  . (4.85)
. (4.85)


