
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Метод избыточных концентрацийСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Наиболее просто и точно задача определения порядка реакции решается в том случае, если скорость реакции может быть получена как функция концентрации только одного из реагентов. Для того, чтобы скорость реакции зависела только от концентрации одного из исходных веществ, обычно используют способ избыточных концентраций, называемый также методом понижения порядка реакций.. По этому методу, предложенному Оствальдом, проводят серию опытов, в каждом из которых изучается влияние концентрации только одного из исходных веществ на скорость реакции. Для этого все остальные исходные вещества берут в таком избытке по сравнению с исследуемым, чтобы их концентрации можно было считать практически постоянными. Определяют порядок реакции по каждому из исследуемых исходных веществ одним из перечисленных ниже способов. Затем определяют общий порядок реакции. Рассмотрим формально простую реакцию n 1-го порядка по веществу
Зависимость этой реакции от концентрации исходных веществ описывается выражением
Общий суммарный порядок реакции равен сумме порядков реакции по отдельным исходным веществам: Проведем реакцию сначала в условиях, когда концентрация исходного вещества
где Затем проводим реакцию при избытке вещества
где Если определить порядок реакции по данному исходному веществу, то можно определить общий порядок реакции, а затем и константу скорости реакции
Методы определения порядка реакции по данному веществу подразделяются на дифференциальные и интегральные в зависимости от того, используют они интегральные или дифференциальные кинетические уравнения для обработки экспериментальных данных зависимости концентрации реагирующих веществ от времени. 4.4.2.2. Дифференциальные методы определения порядка реакции При расчетах этим способом используются расчетные данные для зависимости скорости реакции от времени. На опыте получают зависимость концентрации от времени (кинетическую кривую). Скорость реакции определяется по графику этой зависимости при помощи графического дифференцирования. Тангенс угла наклона касательных, проведенных в разных точках к кинетической кривой, равен производной от концентрации по времени, т. е. равен скорости реакции по данному веществу в данный момент времени. Скорость реакции по данному веществу, например по веществу
Графический метод решения. Прологарифмировав уравнение (4.51), получим
На графике в координатах Если точки найденные по опытным данным, не располагаются на прямой, то это указывает на то, что уравнение не соответствует опытным данным, т. е. скорость реакции зависит от концентрации рассматриваемого вещества по более сложной зависимости. Если скорость реакции заменить на отношение конечных разностей
где Тогда, порядок реакции можно определить следующим образом.Проводим несколько опытов, где измеряем
|
||
|
Последнее изменение этой страницы: 2016-12-10; просмотров: 513; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.007 с.) |

 и n 2 — по
и n 2 — по 
 .
. . (4.47)
. (4.47) . Если реакция является элементарной или формально простой, но подчиняется кинетическому уравнению для элементарной реакции, то порядок по веществам
. Если реакция является элементарной или формально простой, но подчиняется кинетическому уравнению для элементарной реакции, то порядок по веществам  .
. (4.48)
(4.48) частный порядок реакции по первому компоненту.
частный порядок реакции по первому компоненту. (4.49)
(4.49) частный порядок реакции по второму компоненту.
частный порядок реакции по второму компоненту. . (4.50)
. (4.50)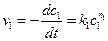 . (4.51)
. (4.51) (4.52)
(4.52) опытные точки для различных моментов времени, в случае справедливости уравнения (4.52), должны располагаться на прямой линии. Отрезок на оси ординат на этом графике дает значение
опытные точки для различных моментов времени, в случае справедливости уравнения (4.52), должны располагаться на прямой линии. Отрезок на оси ординат на этом графике дает значение  а тангенс угла наклона прямой равен порядку реакции
а тангенс угла наклона прямой равен порядку реакции  по веществу
по веществу  . Точно также можно определить
. Точно также можно определить  и
и  .
. , то получим соотношение:
, то получим соотношение: , (4.53)
, (4.53) – среднее изменение концентрации вещества А за период времени
– среднее изменение концентрации вещества А за период времени  ;
;  – средняя за данный промежуток времени концентрация реагирующего вещества.
– средняя за данный промежуток времени концентрация реагирующего вещества. через разные или равные интервалы времени (
через разные или равные интервалы времени ( )– ln
)– ln  , представляет собой прямую линию. Тангенс угла наклона этой прямой равен порядку химической реакции: tg α =
, представляет собой прямую линию. Тангенс угла наклона этой прямой равен порядку химической реакции: tg α = 


