
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Влияние ингибиторов на кинетику ферментативных реакцийСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Вещества, присутствие которых в системе понижает активность фермента, то есть уменьшает скорость реакции, называются ингибиторами. Эффект ингибирования может происходить по разным причинам. 1. Ингибитор I конкурирует с субстратом за активный центр, так как по строению близок к нему и является псевдосупстратом, образуя с ферментом неактивный комплекс: Е + I=ЕI. Константа диссоциации комплекса ЕI называется константой ингибирования:
Начальная скорость реакции в присутствии ингибитора всегда меньше, чем в его отсутствие. Если при увеличении концентрации субстрата в растворе активность фермента восстанавливается, такое ингибирование называется конкурентным. Предельное значение скорости не зависит от присутствия ингибитора:
Уравнение Михаэлиса – Ментена в присутствии ингибитора в этом случае имеет вид:
где
эффективная константа, зависящая от Если Выражение для константы ингибирования выразим из (5.52):
Таким образом, для определения К I, кроме 2. Ингибитор не конкурирует с субстратом за активный центр, так как присоединяется к другой части молекулы белка с образованием неактивных комплексов (EI и ESI), имеющих константы равновесия:
Наличие ингибитора в этом случае приводит к снижению активности фермента, но не изменяет его сродство к субстрату. Если достигается обратимость ингибирования, то есть восстановление активности фермента под действием отличных от субстрата веществ, такое ингибирование называется неконкурентным. Если оба комплекса (EI и ESI) неактивны, то есть не дают продукта, а константы их диссоциации близки между собой ( В этом случае константа Михаэлиса остается постоянной величиной, а изменяется максимальная скорость процесса:
Уравнение Михаэлиса – Ментена в этом случае запишется как
Если Выражение для константы ингибирования получим из (5.55):
Линеаризация уравнения (5.56) и обработка экспериментальных данных для неконкурентного ингибирования в координатах 3. При бесконкурентном ингибировании образуется один не активированный комплекс (ESI) с константой равновесия
Уравнение Михаэлиса – Ментена в этом случае запишется как
где
В этом случае эффективная константа отличается от значения для конкурентного ингибирования, но эффективная скорость выражается уравнением, аналогичным для не конкурентного ингибирования. Линеаризация уравнения (5.59) и обработка экспериментальных данных для неконкурентного ингибирования в координатах
Примеры решения задач. Пример 1. Рассчитайте значение константы Михаэлиса и значение максимальной скорости (
Решение. Для графического решения преобразуем уравнение Михаэлиса – Ментена в линейную форму. 1. Способ Лайнуивера – Берка. Уравнение приводится к виду:
Рассчитанные значения
Отрезок на оси ординат получается равным 1/ v max = 1,45∙106, поэтому v max = 1 / (1,45∙106) = 6,9∙10–7 моль/с. Тангенс угла наклона прямой равен tg α = 2000, следовательно KМ = tg α ∙ v max = 2000 ∙ 6,9∙10–7 = 1,38∙10–3 М.
2. Второй способ Лайнуивера – Берка Строят график по уравнению
в координатах
Из графика получается, что прямая отсекает на оси ординат отрезок, равный
3. Способ Эдди–Хофсти. Уравнение приводится к виду
Строится график в координатах v 0,
График даёт прямую линию, тангенс угла которой равен –1,36∙10–3, а отрезок, отсекаемый на оси ординат, равен 6,86∙10–3. Поэтому. КМ = 1,36∙10–3 М, v max = 6,86∙10–3 моль/с. Бензоат 1,2,5-триметилпиперидола-4 (β-изомер) ингибирует гидролиз бутирилхолина, катализируемый холинэстеразой. Определите тип ингибирования и рассчитайте константу диссоциации комплекса фермент–ингибитор. Экспериментальные данные:
Решение / Рассчитаем константу Михаэлиса и максимальную скорость реакции для различных концентраций ингибитора по способу Эдди–Хофсти. Так как неизвестен способ ингибирования, то используем эффективные значения константы Михаэлиса и максимальной скорости Уравнение Михаэлиса–Ментена приведём к виду (по способу Эдди–Хофсти)
Построим графики зависимостей в координатах (v, Для
Уравнение прямой имеет вид Для
Уравнение прямой v max эф. = 5,23 у.е., K M эф = 0,96∙10–4 М. Для
Уравнение прямой v max эф = 4,40 у.е., K M эф = 0,96∙10–4 М. Для
Уравнение прямой v max эф = 3,16 у.е., K M эф = 0,98∙10–4 М. Для
Уравнение прямой v max эф = 2,41 у.е., K M эф = 0,90∙10–4 М.
Как видно из полученных значений, константа Михаэлиса остаётся неизменной, а максимальная скорость меняется. На этом основании можно сделать вывод, что ингибирование неконкурентное. Рассчитываем константу ингибирования для
Вопросы для самоконтроля 1. Какие соединения получили название «ферменты»? Какова их природа? 2. Перечислите основные классы, на которые разделяются ферменты. Почему их классифицируют не по типу химического строения? 3. Какие вещества называются ингибиторами? Какие различают типы ингибиторов? 4. В каком случае ингибитор называется конкурентным? Укажите схематически механизм этого процесса. 5. Какие три графических способа существуют для определения постоянных 6. Покажите как на основании опытных данных в отсутствие и в присутствии ингибитора определить константы: Гетерогенный катализ Первой наблюдаемой гетерогенно – каталитической реакцией была реакция, осуществленная в 1778 г. Пристли дегидратация этилового спирта на активной глине:
Металлические катализаторы были впервые применены Ван – Марумом (1796 г.) в реакциях дегидрирования этилового спирта на меди, железе, никеле и серебре:
В первой половине XXI века гетерогенному катализу было посвящено большое количество работ. Были открыты окислительные реакции в газовой фазе на металлах (Дэви), разложение аммиака и перекиси водорода (Тенар), гидрирование этилена на платине (Кюльман) и многие другие каталитические процессы. Дальнейшее развитие учения о катализе шло как по пути накопления экспериментальных данных, разработки способов приготовления активных катализаторов, открытия новых каталитических процессов, внедрения их в химическую промышленность, так и по пути развития теории гетерогенного катализа. Но при этом теория развивалась значительно медленней практики, что объясняется отсутствием теории твердого тела. Так как процесс идет по поверхности твердого катализатора, знание строения поверхности катализатора и закономерностей адсорбционных явлений оказывается решающим для развития теории катализа. В настоящее время гетерогенно-каталитические процессы широко применяются в промышленном производстве важнейших химических веществ. В качестве катализаторов применяются переходные металлы, металлы I группы, оксиды, сульфиды, различные группы комплексных соединений и др. Гетерогенно-каталитические процессы более распространены в промышленности, чем процессы гомогенного катализа. Это объясняется тем, что гетерогенные катализаторы более удобны в производстве, их легче отделить от газовой или жидкой среды в непрерывно действующих реакторах.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-10; просмотров: 625; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.108 (0.012 с.) |

 .
. . (5.50)
. (5.50) , (5.51)
, (5.51)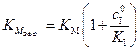 , (5.52)
, (5.52)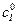 и
и  .
. и
и 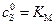 , то скорость реакции ингибирования будет равна
, то скорость реакции ингибирования будет равна  .
.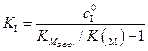 . (5.53)
. (5.53) ,необходимо знать эффективную константу реакции в присутствии ингибитора и константу Михаэлиса в его отсутствие.
,необходимо знать эффективную константу реакции в присутствии ингибитора и константу Михаэлиса в его отсутствие. 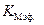 и
и  можно найти, решая задачу графическим методом, например в координатах Лайнуивера – Берга (
можно найти, решая задачу графическим методом, например в координатах Лайнуивера – Берга ( ) для случая процесса с ингибитором и без ингибитора. Константу ингибирования можно рассчитать по уравнению (5.53) или определить непосредственно из графика, так как отношение тангенсов угла наклона прямых в точке пересечения с осью ординат равно
) для случая процесса с ингибитором и без ингибитора. Константу ингибирования можно рассчитать по уравнению (5.53) или определить непосредственно из графика, так как отношение тангенсов угла наклона прямых в точке пересечения с осью ординат равно  .
. (5.54)
(5.54) ), то это равносильно дополнительному условию: ингибитор не мешает взаимодействию субстрата с ферментом, но уменьшает скорость реакции из-за неактивности образующихся комплексов на поверхности фермента.
), то это равносильно дополнительному условию: ингибитор не мешает взаимодействию субстрата с ферментом, но уменьшает скорость реакции из-за неактивности образующихся комплексов на поверхности фермента.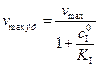 (5.55)
(5.55)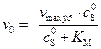 . (5.56)
. (5.56) .
. . (5.57)
. (5.57) позволяет определить
позволяет определить 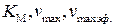 и
и 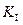 зная
зная  . (5.58)
. (5.58) , (5.59)
, (5.59) . (5.60)
. (5.60)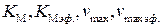 и
и  ) всеми возможными методами для реакции гидролиза метилового эфира N-бензоил-L-аминомасляной, катализируемого α-химотрипсином. Известны данные о зависимости начальной скорости от концентрации субстрата:
) всеми возможными методами для реакции гидролиза метилового эфира N-бензоил-L-аминомасляной, катализируемого α-химотрипсином. Известны данные о зависимости начальной скорости от концентрации субстрата: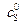 ·103, М
·103, М
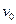 ·107, моль/с
·107, моль/с
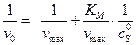
 ,
, 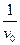 заносим в таблицу и строим график в соответствующих координатах.
заносим в таблицу и строим график в соответствующих координатах.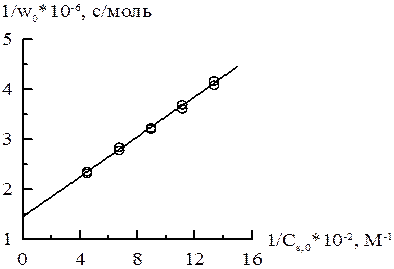
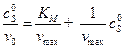
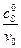 ,
, 

 = 2∙103, а на оси абсцисс отрезок, равный – КМ = – 1,38∙10–3. Поэтому КМ = 1,38∙10–3 М, wmax = 1,38∙10–3/(2∙103) = 6,9∙10–7 моль/с.
= 2∙103, а на оси абсцисс отрезок, равный – КМ = – 1,38∙10–3. Поэтому КМ = 1,38∙10–3 М, wmax = 1,38∙10–3/(2∙103) = 6,9∙10–7 моль/с.
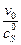 .
.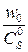 ∙104, л/с
∙104, л/с
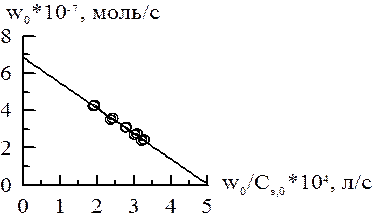
 ·105, М
·105, М
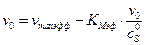
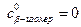 :
: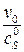 ∙10–4, усл.ед./М
∙10–4, усл.ед./М

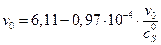 , поэтому получаем v max = 6.11 у.е., KM = 0,97∙10–4 М.
, поэтому получаем v max = 6.11 у.е., KM = 0,97∙10–4 М. М:
М:
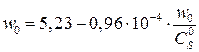 =>
=> М:
М:
 =>
=> М:
М:
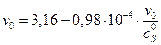 =>
=>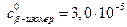 М:
М: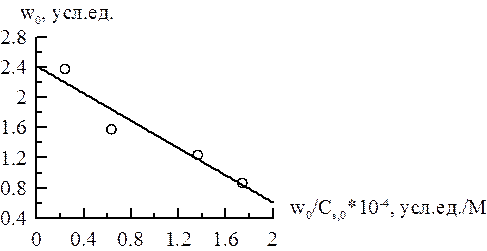
 =>
=>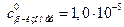 М по уравнению
М по уравнению
 М.
М.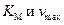 ?
? ?
? .
. C2H5OH ® CH3CHO + H2.
C2H5OH ® CH3CHO + H2.


