
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Кинетика ферментативных реакцийСодержание книги
Поиск на нашем сайте
Рассмотрим самую простую реакцию превращения субстрата (S) в продукт (Р) при участии фермента (Е). Уже в ранних работах было обнаружено, что начальная скорость ферментативной реакции при фиксированной концентрации фермента и малых концентрациях субстрата изменяется линейно с концентрацией субстрата, но для высоких концентраций субстрата скорость реакции уже не зависит от концентрации субстрата. Л. Анри (1903 г.) первым предложил идею, что фермент образует с субстратом промежуточный комплекс. Развил эту идею Л. Михаэлис. Согласно этой идеи, механизм процесса можно представить состоящим из двух стадий. Первая обратимая и быстрая, вторая – необратимая и медленная:
Для данного механизма скорость реакции определяется скоростью образования продукта реакции Р: v Скорость образования промежуточного продукта ES, равна: Уравнения материального баланса для фермента и субстрата имеют вид:
где Решение системы из трех уравнений(5.36 – 5.38) находим из следующих условий: 1) для 2) обычно 3) считают, что концентрация промежуточного соединения Подставляя значение
Поделим числитель и знаменатель этого уравнения на
Величину Подставляя уравнение (5.40) в (5.36), получим уравнение для скорости образования продукта в начальный момент времени:
Анализ уравнения (5.41) позволяет объяснить наблюдаемые на опыте закономерности: 1) если К М>>
то есть начальная скорость линейно зависит от концентрации субстрата. Этот факт полностью подтверждается экспериментальными данными; 2) если
то есть начальная скорость не зависит от концентрации субстрата, что так же соответствует опытным данным. Следовательно, порядок реакции по субстрату в этом случае будет нулевой, а скорость процесса достигает максимального значения. Поэтому уравнение (5.41) можно записать в виде:
Уравнение (6.44) в литературе известно как уравнение Михаэлиса – Ментена. К М называется константой Михаэлиса, физический смысл которой можно сформулировать, анализируя уравнение (5.44). Константа Михаэлиса численно равна концентрации субстрата ( Если для рассматриваемого механизма реакции выполняется условие: Только для ферментов разложения пероксида водорода, каталазы и пероксидазы, для которых Величину Для определения параметров 1. Первый способ (способ Лайнуивера – Берка). Уравнение (5.44) приводят к виду:
График прямой, построенной в координатах
откуда 2. Второй способ (вторая форма уравнения Лайнуивера – Берка). Уравнение (5.45) умножают на
График в координатах
3. Третий способ (способ Эдди - Хофсти). Если умножить обе части уравнения (5.45) на (
График, построенный в координатах ( Указанные способы лианиризации уравнения Михаэлиса – Ментена охватывают различные области концентрации субстрата, когда возможны отклонения от линейности. Поэтому полезно значения Нетрудно показать, что аналогичная (5.45) форма уравнения может быть получена и для более сложных механизмов реакции. Например, когда субстрат взаимодействует с ферментом по схеме:
Выражение для начальной скорости в этом случае имеет вид:
где Возможно протекание более сложных ферментативных реакций с участием двух субстратов.
|
||||||
|
Последнее изменение этой страницы: 2016-12-10; просмотров: 400; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 52.14.145.241 (0.01 с.) |


 . (5.36)
. (5.36) . (5.37)
. (5.37) и
и  , (5.38)
, (5.38) и
и  – начальные концентрации фермента и субстрата,
– начальные концентрации фермента и субстрата, 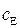 и
и  – их текущие концентрации,
– их текущие концентрации,  –концентрации промежуточного соединения и продукта реакции.
–концентрации промежуточного соединения и продукта реакции. ,
,  , следовательно,
, следовательно,  >>
>>  (или
(или  ), поэтому
), поэтому  ;
; .
. из (5.38) в (5.36) и решая его относительно
из (5.38) в (5.36) и решая его относительно 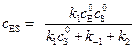 . (5.39)
. (5.39) , тогда имеем:
, тогда имеем: . (5.40)
. (5.40) принято называть константой Михаэлиса.
принято называть константой Михаэлиса. . (5.41)
. (5.41) , (5.42)
, (5.42) , (5.43)
, (5.43) . (5.44)
. (5.44) ), при которой активность фермента составляет половину максимальной, т.е.
), при которой активность фермента составляет половину максимальной, т.е.  . Константой Михаэлиса имеет размерность концентрации, моль/л. Численные значения К М обычно лежат в пределах 10-2 – 10-8 М, легко воспроизводятся и не зависят от концентрации фермента. В то же время К М является функцией температуры, рН среды, зависит от присутствия других веществ, играющих роль ингибитора или активатора.
. Константой Михаэлиса имеет размерность концентрации, моль/л. Численные значения К М обычно лежат в пределах 10-2 – 10-8 М, легко воспроизводятся и не зависят от концентрации фермента. В то же время К М является функцией температуры, рН среды, зависит от присутствия других веществ, играющих роль ингибитора или активатора. >>
>> 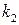 , тогда
, тогда  , где
, где  - субстратная константа, т.е. константа диссоциации фермент–субстратного комплекса на фермент и субстрат, характеризующая меру связывания фермента с субстратом. В общем случае
- субстратная константа, т.е. константа диссоциации фермент–субстратного комплекса на фермент и субстрат, характеризующая меру связывания фермента с субстратом. В общем случае  , причем экспериментальное значение
, причем экспериментальное значение  представляет собой максимальное значение
представляет собой максимальное значение  сильно отличается от субстратной константы
сильно отличается от субстратной константы  – каталитическую константу с той же размерностью.
– каталитическую константу с той же размерностью. используют несколько способов лионеризации уравнения Михаэлиса – Ментена.
используют несколько способов лионеризации уравнения Михаэлиса – Ментена. . (5.45)
. (5.45) , отсекает отрезок на оси ординат, равный
, отсекает отрезок на оси ординат, равный  . Тангенс угла наклона прямой равен
. Тангенс угла наклона прямой равен  . Как следует из уравнения (5.45), константу
. Как следует из уравнения (5.45), константу  имеем соотношение:
имеем соотношение: , (5.46)
, (5.46) .
. . (5.47)
. (5.47) ,
,  , а на оси абсцисс отрезок, равный –
, а на оси абсцисс отрезок, равный –  .
. ), то оно приводится к виду:
), то оно приводится к виду: . (5.48)
. (5.48) ), дает прямую линию, тангенс угла наклона которой равен
), дает прямую линию, тангенс угла наклона которой равен  . Кроме того, как видно из рис. 2, отрезок, отсекаемый на оси абсцисс равен
. Кроме того, как видно из рис. 2, отрезок, отсекаемый на оси абсцисс равен  , так как при
, так как при 
 или
или 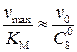 .
. , определенные различными способами, сравнивать между собой.
, определенные различными способами, сравнивать между собой. .
.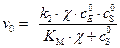 , (5.49)
, (5.49) . Это уравнение аналогично по форме уравнению Михаэлиса – Ментена и также легко линеаризуется.
. Это уравнение аналогично по форме уравнению Михаэлиса – Ментена и также легко линеаризуется.


