
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Кинетика кислотного катализа.Содержание книги
Поиск на нашем сайте
Решение кинетической задачи рассмотрим на примере реакций специфического кислотного[5] катализа. Пусть взаимодействие субстрата (S) и катализатора (H3O+) протекает по схеме:
Скорость лимитирующей стадии определяет скорость протекания процесса: v = k 2 c SH+, (5.23) где k 2 = k ’2·c Концентрация протонизированного субстрата (c SH+) составляет какую–то долю (α) от исходной концентрации субстрата (c S0): α = c SH+/ c S0 или c SH+ = α· c S0. (5.24)
Учитывая это, уравнение для скорости лимитирующей стадии будет равно: v = k 2 α· c S0. (5.25)
Степень протонизации субстрата (α) можно оценить из константы равновесия первой стадии процесса:
Откуда
где Преобразуем уравнение (5.27), используя свойство дробей:
Так как
Подставляя уравнение (5.29) в (5.25) получим выражение для скорости лимитирующей стадии процесса:
Как видно из уравнения (5.30), определяемая из опытных данных эффективная константа скорости зависит от кислотности среды:
Проведем анализ уравнения (5.31). 1. Если равновесие первой стадии устанавливается быстро, то константа равновесия К достаточно большая величина по сравнению с 1, тогда 2. Если равновесие первой стадии устанавливается медленно, то константа равновесия (К) маленькая величина и слагаемым К·h 0 в знаменателе можно пренебречь. В этом случае уравнение (5.31) имеет вид:
После логарифмирования имеем:
где Построив по экспериментальным данным график в координатах lg k эфф – рН, можно оценить значение произведения k 2· K. Если известна к онстанта равновесия первой стадии, то можно определить k 2.· 3. Если константа равновесия К – средняя величина, то уравнение (5.31) можно привести к виду прямой линии:
График, построенный по опытным данным в координатах Кинетика основного катализа Решение кинетической задачи рассмотрим на примере реакций специфического основного катализа. Пусть взаимодействие протонизированного субстрата (SН) и катализатора (ОH–, Н2O, Cl–) протекает следующим образом:
Каждая из этих стадий может лимитировать скорость протекания всего процесса. Заключительные стадии процесса являются равновесными, так как протекают значительно быстрее:
Таким образом, протонизированный субстрат (SH) взаимодействует с тремя разными катализаторами (параллельные химические реакции), поэтому скорость его расходования будет равна сумме скоростей на отдельных стадиях: v SH = v 1+ v 2+ v 3 или v SH= где
Кажущаяся константа скорости определяется из экспериментальных данных. Изучая, как эта константа меняется от Примеры решения задач Пример 1. Химическая реакция СН3СООСН3(aq) + Н2O = СН3СООН(aq) + СН3ОН(aq) катализируется ионами Н+. Полагают, что наблюдаемая константа скорости k ' c вязана с константой скорости некаталитической реакции k соотношением: k' = k (CH+) n. На основании опытных данных определите значения k и п.
Решение. После логарифмирования обеих частей уравнения k' = k (cH+) n, получим
Это соотношение представляет линейную функцию lgk' от п= 1,1» 1 и k · = 1,32·10–4 л·/моль·с. Пример 2 Установлено, что гидролиз очень разбавленного раствора эфира при 25 °С протекает по кислотно-основному механизму катализа, при этом обратная реакция (этерификации) практически не происходит, эфир растворим в воде и в отсутствие катализатора константа скорости реакции практически равна нулю. Процесс протекает по следующей схеме. В случае основного катализа: эфир + ОН– (эфирОН)– +Н2О В случае кислотного катализа: эфир + Н+ (эфир Н)+ + Н2О Экспериментально показано, что скорость гидролиза эфира практически одинакова для значений р Н =1 и р Н=9. Проведите следующие исследования: а) получите выражение для опытной константы скорости реакции и ответьте на вопрос, зависит ли эта константа от р Н раствора; б) определите, чему равна р Н при минимальном значении константы скорости реакции. Какой катализ (ионами Н+ или ОН–) более эффективен в этом случае? Решение. а) На основании предложенной схемы лимитирующими стадиями процесса гидролиза являются реакции (1) и (2), поэтому выражение для скорости реакции имеет вид: v Откуда кажущаяся константа скорости гидролиза эфира равна: где Соотношение (4) показывает, что кажущаяся константа скорости реакции или
б) используя опытные данные, а именно то, что скорость гидролиза эфира практически одинакова для значений р Н =1 и р Н=9, можно из формулы (4) получить отношение констант
откуда
Подставляя численное значение отношения легко вычисляем значение р Н раствора в точке минимума кажущейся константы скорости
Полученный результат объясняет, почему эфиры хранят, например, в парфюмерии при р Н = 5.
|
||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-10; просмотров: 589; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.16.212.203 (0.006 с.) |

 равновесная стадия процесса
равновесная стадия процесса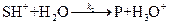 лимитирующая стадия
лимитирующая стадия
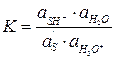 , или
, или  (5.26)
(5.26) или
или  (5.27)
(5.27)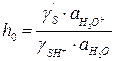 – кислотность среды.
– кислотность среды.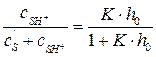 (5.28)
(5.28)
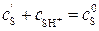 , то степень протонизации субстрата α равна:
, то степень протонизации субстрата α равна: (5.29)
(5.29)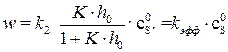 , (5.30)
, (5.30)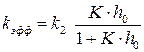 (5.31)
(5.31) .
. .
. , (5.32)
, (5.32)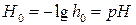 – функция кислотности.
– функция кислотности. (5.33)
(5.33) , в случае соответствия этой модели реальной кинетике процесса должен изображаться прямой линией. Зная угловой коэффициент прямой и отрезок на оси ординат, можно вычислить
, в случае соответствия этой модели реальной кинетике процесса должен изображаться прямой линией. Зная угловой коэффициент прямой и отрезок на оси ординат, можно вычислить 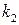 и К.
и К.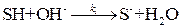 ,
, ,
, .
. ,
, ,
,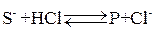 .
. , (5.34)
, (5.34)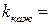
 (5.35)
(5.35) можно оценить каждую из каталитических констант:
можно оценить каждую из каталитических констант: 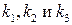 .
. .
. .Если построить график в координатах lg k' –
.Если построить график в координатах lg k' –  (эфирОН)– (1)
(эфирОН)– (1) кислота + спирт + ОН– . – быстрая стадия
кислота + спирт + ОН– . – быстрая стадия (эфир Н)+ (2)
(эфир Н)+ (2) , (3)
, (3)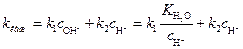 (4)
(4)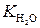 – константа диссоциации воды. При 298 К
– константа диссоциации воды. При 298 К  зависит от р Н раствора, причем
зависит от р Н раствора, причем 
 (5)
(5) (6)
(6) :
: (7)
(7) или
или  (8)
(8) в выражении (6),
в выражении (6), (9)
(9)


