
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Кинетика химических реакций в реакторе идеального вытесненияСодержание книги
Поиск на нашем сайте
Скорость химической реакции по I -му веществу в реакторе идеального вытеснения с постоянной площадью сечения
Это уравнение можно проинтегрировать относительно
Это уравнение позволяет определить изменение концентрации i -го компонента вдоль реактора для реакций любых порядков. Так, например, для реакции первого порядка, протекающей в жидкой фазе (
Потенцируя полученное уравнение, получим:
Для реакции второго порядка (
Концентрацию вещества А на выходе из реактора можно рассчитать по уравнению (4.146), если вместо
Здесь Тогда, например, для реакции первого порядка:
Учитывая, что степень превращения вещества А определяется соотношением:
получим
Для параллельной реакции ®
При протекании реакций в газовой фазе объем реакционной смеси и соответственно объемная скорость Рассмотрим, например, реакцию:
протекающую в газовой фазе. Так как объемная скорость в уравнении (4.145) является постоянной величиной, то введя ее под знак дифференциала получаем:
где
Если реакционная смесь является идеальным газом, то
где Тогда
Если в реактор в единицу времени поступает начальное количество
Для данного сечения реактора количество вещества
Преобразовав это уравнение, получим
где Подставив (4.158) и (4.160) в (4.157), имеем:
Так как
То, подставив (4.161) в (4.154), получим:
Так как температура и давление не изменяются вдоль реактора, то, разделив переменные в уравнении (4.163) и проинтегрировав в пределах от
Это уравнение выражает в неявном виде изменение степени превращения Если
Уравнение (4.165) позволяет рассчитать степень превращения Пример 1. В реакторе идеального смешения происходят следующие реакции
где Начальная концентрация исходного вещества А: Скорость подачи исходных веществ Определить производительность реактора по веществу В и по веществу D. Р е ш е н и е. Производительность реактора по веществу В равна Составим уравнение материального баланса для реактора идеального смешения. На основании стехиометрических соотношений реакций запишем:
где Комбинируя полученные уравнения, получим:
Определим
Производительность реактора по веществу D равна
Определим
Производительность реактора по веществу
Пример 2. Установка состоит из следующих последовательно соединенных реакторов: идеального смешения ( Определить концентрацию исходного вещества после каждого реактора и рассчитать производительность установки по продукту. Р е ш е н и е.
1. Составим материальный баланс для первого и третьего реакторов и решим кинетическое уравнение реакции для реактора идеального вытеснения, если известно время пребывания вещества в реакторе Составим материальный баланс по веществу Для стационарного процесса Отсюда 2. Время пребывания вещества в реакторе идеального смешения для реакции первого порядка равно:
Отсюда:
3. Для третьего реактора идеального смешения материальный баланс запишется:
Тогда 4. Производительность системы по продукту
Кинетика цепных реакций Большое число химических реакций проходит через ряд повторяющихся последовательных и параллельных стадий, образующих повторяющиеся циклы, с участием промежуточных частиц. Наиболее распространены такие процессы, называемые цепными, с участием образующихся в реакционной смеси атомов и радикалов, имеющих свободные валентности и обладающих вследствие этого повышенной реакционной способностью. В стадии образования новой активной частицы свободная валентность сохраняется (правило свободной валентности Семенова). Но возможны процессы, в которых превращение протекает через стадии взаимодействия с энергетически возбужденными, но валентно насыщенными молекулами – энергетические цепи. Возможны сочетания этих двух типов цепей. Радикалы активны и способны вступать во взаимодействие. При таких взаимодействиях, в силу неуничтожимости свободной валентности в системе образуется новый свободный радикал, который также вступает во взаимодействие с образованием свободного радикала. Последовательность таких превращений будет осуществляться до тех пор, пока образовавшийся в одной из стадий свободный радикал не встретится с другим свободным радикалом или не буде захвачен стенкой реакционного сосуда. Таким образом, в системе происходит последовательное превращение одних свободных радикалов в другие. Механизм такого процесса можно представить как регулярное чередование нескольких последовательных реакций, например: Реакции, в которых превращение исходных веществ в продукты реакции, осуществляется путем регулярного чередования реакций с участием свободных радикалов, идущих с сохранением свободной валентности (образованием новой активной частицы), называются цепными реакциями. Примерами цепных, радикальных реакций являются: окисление органических веществ молекулярным кислородом, взаимодействие водорода и углеводородов с хлором и бромом, термическое разложение озона и кислородных соединений хлора, крегинг нефтепродуктов, полимеризация и поликонденсация, некоторые фотохимические и радиационно-химические, ядерные реакции. Цепным процессам присущи некоторые общие особенности: - высокая чувствительность, особенно при малых значениях давления, к присутствию примесей, способных как замедлять, так и ускорять течение реакции; - влияние геометрии (отношение величины поверхности стенок к объему, S / V); - влияние свойств материала реактора, на скорость реакции, особенно при небольших значениях давления. Например, изменение давления или температуры может привести к резкому увеличению скорости превращения, приобретающий взрывной характер. Любая цепная реакция обязательно включает в себя три основные стадии: зарождение (инициирование), развитие цепи и обрыв цепи.
Зарождением (инициированием) называется стадия цепной реакции, в которой образуются свободные радикалы из валентно-ненасыщенных молекул исходных веществ. На этой стадии образуются активные частицы – переносчики цепи. Зарождение цепей может происходить различными путями. 1. Образование активных частиц может происходить при внутримолекулярных взаимодействиях. Так, цепная реакция крекинга этана начинается с мономолекулярного распада этана по связи 2. При бимолекулярном взаимодействии частиц. Цепная реакция окисления уксусного альдегида начинается с образования свободных радикалов при бимолекулярном взаимодействии уксусного альдегида с кислородом:
3. При взаимодействии со стенками реактора. В некоторых случаях процесс зарождения цепей оказывается гетерогенным и идет на стенках реакционного сосуда. Так, в цепных реакциях хлорирования в газовой фазе, например в реакциях
зарождение цепей осуществляется в результате гетерогенной реакции: С12 + стенка 4. За счет воздействия на систему извне. В этом случае процесс зарождения цепей называется инициированием. Например, освещение смеси Если исходные вещества не поглощают света, то инициирование может быть осуществлено путем применения фотосенсибилизатора. Так, добавление паров ртути к смеси пропана с кислородом приводит к фотосенсибилизированному цепному окислению пропана, зарождение цепей в котором происходит в результате реакций
Свободные радикалы могут быть получены при добавлении в систему специальных веществ – инициаторов, легко образующих свободные радикалы. В качестве инициаторов чаще всего используют перекиси, азосоединения, некоторые активные газы ( Инициатором может быть и молекула (частица), сама по себе не распадающаяся на радикалы, но способная реагировать с одним из участников превращения с образованием радикала. Например, при окислении углеводородов (RH) такую роль выполняют ионы кобальта: Отметим также, что образование радикала в первичной реакции не всегда дает частицу, определяющую продолжение цепи. Так, при крекинге этана Использование химических инициаторов особенно удобно в тех случаях, когда необходимо точно знать скорость инициирования. Скоростью инициирования называется число активных центров (радикалов), образующихся в единице объема, в единицу времени.
Скорость зарождения цепей можно описать уравнениями первого и второго порядков. Так, например, для процесса
скорость зарождения цепи описывается уравнением Для реакции
скорость зарождения цепи будет равна Реакциями развития (продолжения) цепей называются стадии цепной реакции, когда активные частицы взаимодействуют с молекулами исходных веществ с образованием новых активных частиц и продуктов реакции. К реакциям продолжения цепей относятся также реакции, в которых одна активная частица заменяется другой, но при этом не расходуются молекулы исходного вещества или (и) не образуются молекулы продукта. Возможны четыре типа реакций. 1. Взаимодействие свободного радикала R или атома с молекулой исходного вещества с образованием нового радикала, причем образование продукта не обязательно:
2. Взаимодействие свободного радикала R или атома с молекулой исходного вещества с образованием не только нового радикала или атома, но и молекулы продукта:
3. Изомеризация радикала с возможным образованием продукта:
4. Мономолекулярный распад радикала с образованием продукта превращения и нового радикала или атома: 5. Мономолекулярный распад радикала с образованием продукта превращения Молекулы исходных веществ расходуются в реакциях 1 и 2 типов, а продукты образуются в превращениях типа 3, 4. В любом цепном процессе должны присутствовать хотя бы по одной (могут быть и обе) из стадий расхода исходного вещества и образования продукта. Например, при термическом распаде (крекинге) этана, реакциями продолжения цепи являются:
Скорость этих элементарных реакций описывается уравнениями:
Здесь, в первой реакции радикал водорода взаимодействует с исходным веществом с образованием нового радикала Совокупность многократно повторяющихся стадий продолжения цепи, из которых складывается цепная реакция, называется звеном цепи. Звеном цепи, например, является приведенная выше совокупность стадий:
Если в результате химических реакций, составляющих звено цепной реакции, количество радикалов в системе не увеличивается, то такая реакция называется цепной реакцией с неразветвленными цепями. Если в результате элементарных актов, составляющих звено цепи, образуется две или более активные частицы, то такая реакция называется цепной реакцией с разветвленными цепями.
В результате первой реакции, вместо одной свободной валентности у атома водорода, образуются три свободные валентности – одна у свободного гидроксила Развитие цепи удобно характеризовать длиной цепи.
Число молекул данного исходного вещества, которые прореагировали в результате одного элементарного акта зарождения цепи (число циклов от зарождения цепи (образования активной частицы) до ее обрыва) называется длиной цепи. Введем в начале понятие средней длины цепи, как среднее число актов продолжения цепи от появления активной частицы на стадии зарождения до обрыва. Обозначим число актов продолжения цепи как
а вероятность обрыва цепи:
При стационарности процесса
Среднюю длину цепи –(s) тогда определяем как математическое ожидание случайной величины s с вероятностью
Если вероятность обрывамала, то
Т.к. значение Как отмечалось выше, в стадиях продолжения неразветвленных цепных реакциях количество радикалов не меняется. Если в каждом звене образуется одна молекула продукта, то цепь дает s молекул продукта. Обозначим число активных частиц, образующихся в единицу времени, как
и будет определяться характеристиками стадий зарождения и обрыва цепей. Анализ вышесказанного позволяет сделать ряд выводов. 1. Скорость реакции можно повысить за счет увеличения скорости зарождения цепей малыми добавками веществ, способных давать свободные радикалы. 2. Скорость реакции существенно возрастает при внешних воздействиях, способствующих образованию свободных радикалов (свет, ионизирующие облучения и т.п.). 3. Скорость реакции зависит от геометрии реактора, материала стенок и присутствия на них посторонних веществ, особенно это сказывается при малых давлениях в газовой фазе, поскольку при этом длина свободного пробега велика и молекулы легко достигают стенок, где может произойти обрыв цепи. 4. Скорость реакции резко уменьшается в присутствии добавок, способствующих гибели активных частиц; это свойство часто используют для доказательства протекания цепного механизма процесса. Обрывом цепи называются процессы, приводящие к исчезновению активных частиц. Обрыв цепей в основном происходит в результате: - захвата свободного радикала или атома стенкой реакционного сосуда; - взаимодействия с другой активной частицей при тройном столкновении; - взаимодействия с валентно-насыщенными молекулами. Различают линейный (первый порядок по концентрации активных частиц) и квадратичный (второй порядок) обрыв цепи. Линейный обрыв цепей на стенках сосуда имеет определяющее значение в цепных газовых реакциях, идущих при невысоких давлениях, когда длина свободного пробега соизмерима с размерами реактора. Механизм обрыва цепей по этому типу сводится к адсорбции активной частицы на стенке сосуда с последующей рекомбинацией двух активных частиц: адсорбированной и вновь поступающей из газовой фазы. Понятно, что скорость этого процесса будет пропорциональна частоте ударов о стенку, т.е. общему давлению в первой степени (реакция первого порядка). Реакция обрыва на стенке является гетерогенной стадией. Очевидно, что в таком процессе можно выделить две стадии: диффузию частиц к поверхности и превращение на поверхности. Соответственно, в зависимости от того, какая стадия будет протекать медленнее, различают диффузионную (более медленной стадией является диффузия) и кинетическую (более медленной является стадия взаимодействия радикала и стенки) области стадии обрыва цепей. Скорость обрыва по второму механизму должна зависеть от величины поверхности реактора. Более строгим критерием будет отношение величины площади поверхности стенок к объему реактора S / V. В кинетической области скорость обрыва прямо пропорциональна этому параметру. Поскольку гибель свободного радикала на поверхности является химическим процессом, то скорость может зависеть от свойств материала стенки, содержащихся на ней примесей, оказавшихся случайно (промывка реактора перед опытом) или нанесенных преднамеренно. Это свойство характеризуется величиной ε-вероятностью захвата свободных радикалов стенкой, значение которой может изменяться в широких пределах. При достаточно больших давлениях обрыв цепей происходит в объеме и сводится к взаимодействию активных частиц (рекомбинации) в присутствии третьей частицы, например:
где М – одна из молекул газовой системы. Скорость такого процесса пропорциональна квадрату концентрации активных частиц (квадратичный обрыв) Обрыв цепей может происходить при введении в реакционную систему валентно насыщенных молекул - ингибиторов. Вещества, введение которых в идущую цепную реакцию приводит к замене активных свободных радикалов, развивающих цепь, на малоактивные, не способные к продолжению цепей, называются ингибиторами цепных реакций. Примером цепной реакции может служить процесс образования хлористого водорода из водорода и хлора. Смесь этих газов при комнатной температуре и в темноте совершенно стабильна, но бурно реагирует при облучении или после введения в нее очень малого количества паров натрия: 1.
2. 3. 4. 5. При протекании стадии 1 происходит зарождение цепи. Затем идет развитие цепи [стадии (2-4)]. В стадии (5) происходит обрыв цепи. В реакции образования хлористого водорода бурному ее протеканию способствует довольно большая изотермичность, составляющая 92,3 кДж/моль, в результате чего процесс заканчивается взрывом. В данной схеме приведены не все возможные реакции. В приведенном механизме не учитывается первичная диссоциация водорода
|
|||||||||
|
Последнее изменение этой страницы: 2016-12-10; просмотров: 746; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.174.57 (0.015 с.) |

 равна:
равна: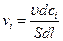 (4.145)
(4.145)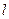 . Тогда
. Тогда . (4.146)
. (4.146) ;
;  ), получим:
), получим: . (4.147)
. (4.147) (4.148)
(4.148) ;
;  ), получим:
), получим: . (4.149)
. (4.149) . Тогда, с учетом того, что
. Тогда, с учетом того, что  , получим:
, получим: . (4.150)
. (4.150) рассчитывается для условий, соответствующих условиям на выходе из реактора. Приведенное уравнение может быть использовано для определения среднего времени пребывания реагента в реакторе и, соответственно, размеров реакционного пространства, а также для определения состава реакционной смеси на выходе из реактора.
рассчитывается для условий, соответствующих условиям на выходе из реактора. Приведенное уравнение может быть использовано для определения среднего времени пребывания реагента в реакторе и, соответственно, размеров реакционного пространства, а также для определения состава реакционной смеси на выходе из реактора. ,
, 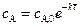 , (4.151)
, (4.151)
 ,
,  (4.152)
(4.152) :
: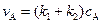 ),
),  ,
,  . (4.153)
. (4.153) может изменяться по мере ее движения в реакторе. Это изменение нужно учитывать при выводе кинетических уравнений.
может изменяться по мере ее движения в реакторе. Это изменение нужно учитывать при выводе кинетических уравнений.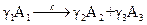 ,
, , (4.154)
, (4.154) - количество молей вещества
- количество молей вещества 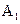 , проходящее через любое сечение реактора в единицу времени. Обозначив
, проходящее через любое сечение реактора в единицу времени. Обозначив  , выразим
, выразим  через
через  , тогда
, тогда . (4.155)
. (4.155) , (4.156)
, (4.156) - общее количество молей всех веществ, проходящих через сечение реактора в единицу времени.
- общее количество молей всех веществ, проходящих через сечение реактора в единицу времени.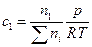 . (4.157)
. (4.157) молей вещества
молей вещества  , называемая степенью превращения вещества
, называемая степенью превращения вещества 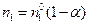 . (4.158)
. (4.158)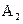 равно -
равно -  ; количество вещества
; количество вещества  равно
равно 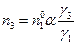 . Суммируя количества всех веществ, получим:
. Суммируя количества всех веществ, получим: . (4.159)
. (4.159)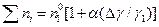 , (4.160)
, (4.160)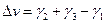 .
. . (4.161)
. (4.161)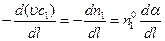 , (4.162)
, (4.162)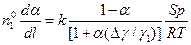 . (4.163)
. (4.163) до
до  до
до 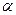 , получим:
, получим: . (4.164)
. (4.164) , а
, а  - степень превращения на выходе из реактора, то
- степень превращения на выходе из реактора, то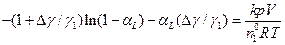 . (4.165)
. (4.165)
 целевой продукт реакции.
целевой продукт реакции.  .
. = 1 кмоль/ м3. Текущие концентрации веществ:
= 1 кмоль/ м3. Текущие концентрации веществ: 


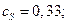
 кмоль/
кмоль/  .
.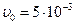
 .
.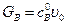 , а по веществу D –
, а по веществу D – 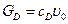 . Неизвестные концентрации
. Неизвестные концентрации  и
и  можно определить из уравнения материального баланса.
можно определить из уравнения материального баланса. ;
;  ;
;  ;
;  ;
;  ,
, - промежуточные концентрации веществ.
- промежуточные концентрации веществ. ;
;
 кмоль/м
кмоль/м  .
. кмоль/с.
кмоль/с.
 равна
равна кмоль/с.
кмоль/с. ), идеального вытеснения (
), идеального вытеснения ( ). Начальная концентрация вещества
). Начальная концентрация вещества 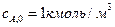 , скорость подачи
, скорость подачи 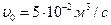 . В реакторах протекает реакция первого порядка
. В реакторах протекает реакция первого порядка  . Константа скорости реакции
. Константа скорости реакции  . В начальный момент времени продукт в системе отсутствует, плотность реакционной системы в ходе реакции не меняется.
. В начальный момент времени продукт в системе отсутствует, плотность реакционной системы в ходе реакции не меняется. .
.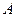 для первого реактора.
для первого реактора. .
. =
=  кмоль/м3.
кмоль/м3. .
.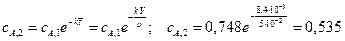
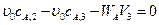 .
. .
. .
.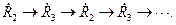
 .
. или
или  .
. +
+  —>2НС1
—>2НС1 CI +
CI +  адс
адс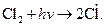
 ,
, 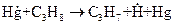
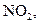
 ), металлы с переменной валентностью.
), металлы с переменной валентностью. .
.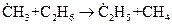 первичным радикалом является
первичным радикалом является  , а в продолжении участвуют радикалы, образующиеся в результате вторичных реакций.
, а в продолжении участвуют радикалы, образующиеся в результате вторичных реакций.  ,
, 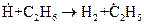 .
.
 .
.
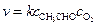 .
.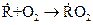 или
или  .
.
 .
.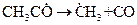 или
или 
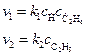 .
. . Во второй реакции, один радикал заменяется на другой и образуется молекула продукта.
. Во второй реакции, один радикал заменяется на другой и образуется молекула продукта.
 и две у атома кислорода
и две у атома кислорода  . Вторая реакция приводит к появлению двух одновалентных частиц. Реакции разветвления могут быть свойственны самой системе (горение водорода) или же вызываться посторонним воздействием.
. Вторая реакция приводит к появлению двух одновалентных частиц. Реакции разветвления могут быть свойственны самой системе (горение водорода) или же вызываться посторонним воздействием. , и число актов обрыва цепи как
, и число актов обрыва цепи как 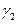 . Вероятность продолжения цепи равна:
. Вероятность продолжения цепи равна: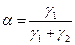 , (4.165)
, (4.165) . (4.166)
. (4.166) , и
, и  . Вероятность- (p), того, что цепь состоит из s звеньев продолжения и одной стадии обрыва, можно рассчитать по формуле:
. Вероятность- (p), того, что цепь состоит из s звеньев продолжения и одной стадии обрыва, можно рассчитать по формуле: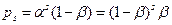 . (4.167)
. (4.167) :
:
 . (4.168)
. (4.168) . Прологарифмируем уравнение (4.167)и продифференцируем полученное выражение по s. Получим:
. Прологарифмируем уравнение (4.167)и продифференцируем полученное выражение по s. Получим: . (4.169)
. (4.169)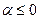 , то наиболее вероятны короткие цепи. Максимальная длина цепи равна
, то наиболее вероятны короткие цепи. Максимальная длина цепи равна  . Известны реакции, длина цепи в которых составляет
. Известны реакции, длина цепи в которых составляет  (например, взаимодействие хлора с водородом или с СО). Длина цепи зависит от различных факторов, в том числе и от концентрации исходного вещества (увеличение скорости квадратичного обрыва). Так при пиролизе этана при исходном давлении 57 мм.рт.ст. средняя длина цепи равна 9,8, а при давлении 454 мм.рт.ст. средняя длина цепи равна 4,1.
(например, взаимодействие хлора с водородом или с СО). Длина цепи зависит от различных факторов, в том числе и от концентрации исходного вещества (увеличение скорости квадратичного обрыва). Так при пиролизе этана при исходном давлении 57 мм.рт.ст. средняя длина цепи равна 9,8, а при давлении 454 мм.рт.ст. средняя длина цепи равна 4,1.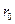 . Тогда при малой вероятности обрыва цепи скорость неразветвленной цепной реакции равна:
. Тогда при малой вероятности обрыва цепи скорость неразветвленной цепной реакции равна: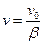 (4.170)
(4.170)
 или
или  .
. или
или
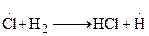

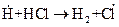

 и
и 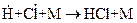 . Эти процессы вследствие малой концентрации атомов водорода, обусловленной их высокой активностью, не могут конкурировать с процессами 3 и 4.
. Эти процессы вследствие малой концентрации атомов водорода, обусловленной их высокой активностью, не могут конкурировать с процессами 3 и 4.


