
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Формальная кинетика элементарных и формально простых гомогенных односторонних реакций в закрытых системахСодержание книги
Поиск на нашем сайте
Для нахождения закона, который описывает кинетику изучаемой реакции, необходимо з аписать выражение для скорости реакции: а) согласно определению скорости реакции
б) исходя из основного постулата формальной кинетики: в) приравнять друг другу эти уравнения, разделить переменные и проинтегрировать полученное уравнение. 4.4.1.1. Кинетика односторонних реакций первого порядка Для элементарной, необратимой реакции первого порядка
скорость реакции связана со скоростью образования вещества
На основании постулата формальной кинетики скорость односторонней реакции первого порядка равна:
Приравнивая эти уравнения и опуская для простоты индекс А, получаем
Разделив переменные и проинтегрировав левую и правую части полученного уравнения в пределах от
или
где Потенцируя уравнение (1.12), получим кинетическое уравнение, описывающее зависимость концентрации исходного вещества от времени в явном виде:
Константа скорости реакции первого порядка имеет размерность При кинетическом исследовании реакций первого порядка вместо концентрации можно использовать любые другие величины, пропорциональные концентрации, т. к. в уравнения (1.12) входит отношение концентраций. Например, концентрации можно заменить количеством исходного вещества
где х – количество прореагировавшего вещества в молях,
Константу скорости можно выразить так же через долю вещества, распавшегося к моменту времени t:
Константа скорости в этом случае равна:
В ряде случаев оценить точное значение
где Для характеристики скорости реакции первого порядка наряду с константой скорости часто пользуются временем полупревращения (период полураспада) – t 1/2. Это время, в течение которого прореагирует половина начального количества вещества (С t = 0,5 С 0). Из уравнения (4.30) получаем:
Из уравнения (4.31) видно, что период полупревращения для реакций первого порядка не зависит от начальной концентрации исходного вещества. Уравнения (4.25, 4.27, 4.28) позволяют рассчитать концентрацию исходного вещества и продуктов реакции, скорость реакции в любой момент времени, если известна константа скорости реакции, то есть решить прямую задачу химической кинетики. Используя уравнения (4.24, 4.26-4.29) можно решить и обратную задачу – выяснить возможность описания зависимости
Полученное уравнение в координатах
Рис. 4. Рис. 5. Зависимость концентрации (рис. 4) и логарифма концентрации (рис. 5) исходного вещества от времени для реакции первого порядка.
|
||
|
Последнее изменение этой страницы: 2016-12-10; просмотров: 451; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.5 (0.008 с.) |

 ,
,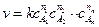 ,
,
 соотношением
соотношением . (4.20)
. (4.20) . (4.21)
. (4.21) . (4.22)
. (4.22) до
до  и от 0 до
и от 0 до  получаем
получаем ; (4.23)
; (4.23) , (4.24)
, (4.24) — концентрация исходного вещества к моменту времени t.
— концентрация исходного вещества к моменту времени t. . (4.25)
. (4.25) . При этом время реакции может измеряться как в часах, так и в долях секунды, в веках и др. Величина, обратная константе скорости реакции первого порядка, имеет размерность времени и называется средней продолжительностью жизни отдельной частицы.
. При этом время реакции может измеряться как в часах, так и в долях секунды, в веках и др. Величина, обратная константе скорости реакции первого порядка, имеет размерность времени и называется средней продолжительностью жизни отдельной частицы. , где V – объем системы. Тогда для константы скорости реакции получаем выражение
, где V – объем системы. Тогда для константы скорости реакции получаем выражение (4.26)
(4.26) - количество вещества в молях, которое осталось во всем объеме системы к моменту времени t. Из уравнения (1.14) легко получить выражение для зависимости количества прореагировавшего вещества от времени:
- количество вещества в молях, которое осталось во всем объеме системы к моменту времени t. Из уравнения (1.14) легко получить выражение для зависимости количества прореагировавшего вещества от времени: . (4.27)
. (4.27)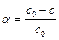 . (4.28)
. (4.28) . (4.29)
. (4.29) или с0 невозможно. В этих случаях используют выражение:
или с0 невозможно. В этих случаях используют выражение: (4.30)
(4.30) ,
,  и
и  ,
,  - количества и концентрации исходных веществ для времени t 1 и t 2 соответственно, причем выбор времени не имеет значения.
- количества и концентрации исходных веществ для времени t 1 и t 2 соответственно, причем выбор времени не имеет значения. , t 1/2 =
, t 1/2 =  . (4.31)
. (4.31) . Зная концентрацию реагента или скорость реакции можно определить константу скорости реакции, являющуюся кинетическим параметром этой зависимости. Для этого, уравнение (4.24) запишем как
. Зная концентрацию реагента или скорость реакции можно определить константу скорости реакции, являющуюся кинетическим параметром этой зависимости. Для этого, уравнение (4.24) запишем как . (4.32)
. (4.32) представляет собой уравнение прямой линии. Значения
представляет собой уравнение прямой линии. Значения  можно найти по тангенсу угла наклона прямой, построенной по опытным данным в координатах
можно найти по тангенсу угла наклона прямой, построенной по опытным данным в координатах 




