
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Термодинамический аспект теории активированного комплекса.Содержание книги
Поиск на нашем сайте
Если константа скорости имеет размерность см3/моль×с и все вещества находятся в стандартном состоянии (
где Множитель В справочнике физико-химических величин нет значений внутренних энергий активации образования молекул активированного комплекса. Поэтому вместо
а затем продифференцируем (4.220) по температуре и сравним с уравнением Аррениуса (4.65):
Из сравнения следует, что
Подставив (4.222) в (4.219), получим выражение для константы скорости на основе теории активированного комплекса для реакции, протекающей при постоянном объеме:
Множитель Р = Если реакция протекает в газовой фазе, то в качестве стандартного состояния используют р 0 = 1 атм. Тогда
Поэтому энтальпия активации связана с опытной энергией активации соотношением:
В этом случае для расчета констант из таблиц берут обычно значения энтропии веществ, стандартизованные по давлению, в связи с чем приходится переходить от величин
Если Подставив (4.225), (4.227) в уравнение (4.219), получим выражение для расчета константы скорости в случае реакции, протекающей в газовой фазе:
Из формулы (4.228) нетрудно получить формулу для расчета
Рассмотрим применение формулы (4.228) к описанию кинетики различных реакций. 1. Для мономолекулярной реакции, в которой образование активированного комплекса происходит без изменения числа частиц (n =1):
Значение опытной энергии активации (Е) связано с энтальпией активации (n =1) соотношением:
Для мономолекулярных реакций 2. В случае бимолекулярной реакции (n =2) из двух молекул газа образуется одна молекула активированного комплекса, поэтому константа скорости может быть вычислена по формуле:
Для бимолекулярной реакции энтальпия активации связана с опытной энергией активации соотношением (р 0 =1 атм):
3. Для реакций, протекающих в растворах, константу равновесия
Примеры решения задач. Пример 1. Триметилгидропероксид
Реакция протекает в водном растворе при рН =1. Константа скорости этой реакции при Т =298 К равна 16,4 л/(моль×с), опытная энергия активации 38,6 кДж/моль. Плотность гидропероксида 1,226 г/см3, M = 84 г/моль, плотность раствора, содержащего Fe2+, равна 1,2135, М= 56 г/моль. Рассчитать долю активных столкновений из общего числа столкновений, константу скорости данной реакции по теории активных столкновений при Т =298 К и оцените стерический множитель Р. Р е ш е н и е. 1. Эффективный диаметр столкновений рассчитаем по плотности гидропероксида и раствора железа (+2):
=5,099∙10-8 см. Откуда: 2. Опытная энергия активации связана с теоретической соотношением:
3. Доля активных столкновений из общего числа столкновений молекул равна:
4. Константу скорости по теории активных столкновений рассчитаем по формуле для случая столкновения двух разных молекул:
k = 6,022·1023·2,6·10-15 6,67 ×106 5. Стерический множитель Р рассчитаем по формуле: Значение предэкспоненциального множителя равно: Частота стокновений равна: =10-3·6,022·1023·2,6·10-15 Стерический множитель Р равен:
Вывод: Реакция взаимодействия триметилгидропероксида с двухвалентным железом относится к бимолекулярным реакциям с валентно-насыщенными молекулами, для которых характерно высокое значение энергии активации и малое значение стерического множителя Р. Пример 2. Для элементарной бимолекулярной реакции
получены опытные значения предэкспоненциального множителя А =1,56·1011(л/моль·с) и энергия активации Е =78,9 Кдж/моль при р 0= 1 атм. Рассчитайте с помощью теории активированного комплекса при 689 К: а) энтальпию активации Р е ш е н и е. Выскажем предположение, что 1. Рассчитаем значение константы скорости по формуле:
2. Энтальпия активации
где n – молекулярность реакции. В данном случае n =2. Тогда
3. Энтропия активации равна:
= -143,97 Дж/моль×К. 4. Если стандартное состояние С 0 = 1 моль/л, то R4 =0,082 л∙атм/ моль·К, тогда:
5. 6.
Вопросы и задания для самоконтроля. 1. В чем заключается основная идея теории активных столкновений? 2. Совпадают ли константа скорости, рассчитанная по теории активных столкновений с константой скорости, определенной из опыта? 3. Физический смысл стерического фактора Р. 4. В чем заключается основная идея теории переходного состояния? Есть ли различие в понятиях «переходное состояние» и «активированный комплекс»? 5. Приведите уравнение, связывающее константу скорости с энтропией активации и опытной энергией активации. 6. Гидролиз метана при температуре 1200 К отвечает кинетике реакции первого порядка. Используя опытные значения энергии активации Е = 335 кДж/моль и значение предэкспоненциального множителя Глава 5. Катализ Основные понятия и особенности катализа Катализ имеет огромное значение в природе и технике. Каталитическими являются процессы синтеза белков и обмен веществ в биологических системах; процессы глубокой переработки нефти с помощью крегинга, гидроочистки, гидрокрегинга и риформинга; синтез и окисление аммиака; производство серной кислоты и метанола; гидролиз сложных эфиров; гидрирование олефинов, и т. д. В настоящее время около 80 % всей химической продукции получается с помощью каталитических процессов. Каталитические реакции были известны в глубокой древности, однако систематически изучать их начали только в начале прошлого (XXI) века. Термин ²катализ² ввёл Берцелиус в 1836 г. Современное определение катализа сформулировано в работах Г.К. Борескова. Катализ –это явление возбуждения химической реакции или изменения их скорости под влиянием веществ – катализаторов, многократно вступающих в промежуточное химическое взаимодействие с участниками реакции и восстанавливающих свой химический состав после каждого цикла промежуточного взаимодействия. В данном определении подчеркивается, что каталитические процессы имеют химическую природу взаимодействия катализатора и реагента. Однако катализатор – это вещество, поэтому теплота и свет, хотя и влияют на скорость протекания реакции, не являются катализаторам. Катализатор не расходуется в результате химической реакции, Различные каталитические процессы имеют ряд общих характерных особенностей, связанных в основном с особой ролью катализатора и закономерностями его действия при протекании химических реакций. При каталитических процессах отсутствуют стехиометрические соотношения между количеством катализатора и реагирующими веществами, так как катализатор во время процесса не расходуется и остаётся химически неизменным. Однако свое физическое состояние катализатор может изменять, например, он может спекаться, отравляться и т. д. Важно отметить, что возможные изменения представляют собой побочные явления, не связанные с его каталитическим действием. 1. Катализатор не влияет на константу равновесия химической реакции, так как стандартное изменение энергии Гиббса процесса (D G) без катализатора и в его присутствии будет одинаковым. Причина каталитического действия (резкое увеличение константы скорости реакции) связано с изменением механизма реакции в присутствии катализатора по пути, характеризуемом минимальной высотой энергетического барьера. При этом взаимодействие реагента с катализатором переводит вещество в более активную частицу. Речь идет не о переведении реагента в возбужденное состояние, а об образовании нестойкого в условиях реакции нового химического соединения. Строго говоря, увеличение константы скорости можно объяснить либо уменьшением энергии активации процесса, либо увеличением энтропии активации. Согласно теории абсолютных скоростей реакций, константа скорости реакции (k) равна:
где E = ΔH* – энергия активации химической реакции или теплота образования активированного комплекса; А – предэкспоненциальный множитель, который определяется из уравнения: A = A 0 eDS*/R, (5.2) или в логарифмической форме
где Более существенно изменение механизма протекания реакции в присутствие катализатора, приводящее к снижению энергии активации реакции. Так, например, в реакции разложения H2O2 в присутствии катализатора (фермента каталазы) энергия активации понижается от 72 до (4¸8) кДж/моль. Это соответствует увеличению скорости реакции в 1023 раз при постоянстве предэкспоненциального множителя (А). В среднем, энергия активации некаталитических процессов равна 200¸300 кДж.; гетерогенно-каталитических 60¸80 кДж, а ферментативных реакций 30¸40 кДж. Таким образом, действие катализатора сводится к тому, что из всего многообразия различных путей протекания реакции, катализатор реализует путь с наименьшей высотой активационного барьера. Примеры решения задач. Пример 1. Установлено, что энергия активации разложения карбамида в присутствии катализатора уреазы уменьшается в четыре раза. Оценитьпри какой температуре необходимо проводить эту же реакцию разложения, чтобы она протекала с такой же скоростью, как и каталитическая реакция при температуре 298 К? Решение. Запишем для каталитической реакции в присутствии уреазы уравнение Аррениуса В отсутствие уреазы это уравнение примет вид[3]:
где Е2 – энергия активации, отличная, от Е 1; Т2 – температура, при которой k 2= k 1. Приравнивая левые части обоих уравнений, после логарифмирования получим:
Подставляя значение Пример 2. Для некоторой химической реакции присутствие катализатора позволяет уменьшить энергию активации химического процесса, реализуемого при температуре 500 °С, от 50 до 35 кДж. Покажем: а) во сколько раз увеличится скорость каталитической реакции по сравнению с некаталитической, полагая, что все другие факторы скорости реакции остаются неизменными; б) при какой температуре каталитическая реакция протекала бы с такой же скоростью, что и некаталитическая при 500 °С; в) какие преимущества дает использование катализатора? Решение. а) Пусть для некаталитической реакции уравнение Аррениуса имеет вид:
В присутствие катализатора это уравнение имеет вид:
Если поделим уравнение (1) на уравнение (2), то после логарифмирования получим:
Используем уравнение Аррениуса, связывающее кинетические параметры следующим б) найдем температуру, при которой k2будет иметь такое же значение, что и k 1при 500 °С (или 773 К). Это означает, что надо найти температуру Т 2,для которой То есть
или
в) использование катализатора позволяет понизить температуру, не уменьшая скорости процесса, что приведет к экономии энергии (особенно это важно для промышленных процессов). Пример 3. Экспериментально установлено, что реакция 2Се4+ + Тl = 2Се3+ + Т13+ (1) протекает в растворе очень медленно, но ускоряется в присутствии ионов Ag+, причем скорость становится пропорциональной концентрации ионов Ag+. На основании предложенного механизма для этой реакции Ag++ Се4+ Ag2+ + Tl+ Tl2+ + Се4+ Необходимо вывести кинетическое уравнение для образования продукта реакции (1), ионов Т13+. Решение. Скорость образования продукта Т13+ можно записать как
Ион Т12+образуется только по стадии (2) и вступает в реакцию лишь на стадии (3), поэтому скорости этих двух стадий выравниваются, т.е.
Концентрацию другого промежуточного соединения, Ag2+, находим, используя принцип квазистационарных концентраций:
Подставляя значение
Значение отношения констант
Полученное кинетическое уравнение подтверждает опытный факт прямо пропорциональной зависимости скорости образования продуктов от концентрации катализатора — ионов Ag+. Вопросы для самоконтроля 1. Дайте классические определения терминов «катализ» и «катализатор». Являются ли теплота и свет катализаторами? 2. Оказывает ли катализатор влияние на термодинамические условия процесса? Смещает ли он положение равновесия? Может ли он изменить выход продукта реакции? Ответ объясните. 3. В чем заключается причина увеличения скорости химической реакции в присутствии катализатора?
|
||||
|
Последнее изменение этой страницы: 2016-12-10; просмотров: 1576; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 52.15.71.146 (0.012 с.) |

 =1 моль/см3), то для реакции, протекающей при постоянном объеме:
=1 моль/см3), то для реакции, протекающей при постоянном объеме: . (4.219)
. (4.219) – стандартная энергия активации Гельмгольца;
– стандартная энергия активации Гельмгольца;  – энтропия активации при стандартном состоянии (
– энтропия активации при стандартном состоянии ( – внутренняя энергия активации;
– внутренняя энергия активации;  = (1- n) – изменение числа молекул при образовании активированного комплекса; n – число вступающих в реакцию молекул.
= (1- n) – изменение числа молекул при образовании активированного комплекса; n – число вступающих в реакцию молекул. в формуле (4.219) необходим, чтобы получить одинаковую размерность в правой и левой частях равенства.
в формуле (4.219) необходим, чтобы получить одинаковую размерность в правой и левой частях равенства. при расчетах констант скоростей приходится пользоваться опытными энергиями активации. Чтобы найти связь между этими величинами, прологарифмируем уравнение (4.218)
при расчетах констант скоростей приходится пользоваться опытными энергиями активации. Чтобы найти связь между этими величинами, прологарифмируем уравнение (4.218) , (4.220)
, (4.220) . (4.221)
. (4.221) (4.222)
(4.222) . (4.223)
. (4.223) равен предэкспоненциальному множителю уравнения Аррениуса, а энтропийный множитель это стерический фактор Р:
равен предэкспоненциальному множителю уравнения Аррениуса, а энтропийный множитель это стерический фактор Р: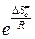 . (4.224)
. (4.224) . (4.225)
. (4.225) . (4.226)
. (4.226) . В применении к газовым реакциям будет иметь место соотношение:
. В применении к газовым реакциям будет иметь место соотношение: , (4.227)
, (4.227) , то
, то  , где R 3 = 82 см3∙атм/моль·К.
, где R 3 = 82 см3∙атм/моль·К. см3/моль·с. (4.228)
см3/моль·с. (4.228) Дж/моль×К. (5.36 4.229)
Дж/моль×К. (5.36 4.229) . (4.230)
. (4.230) . (4.231)
. (4.231) , а стерический фактор Р вычисляется по формуле (4.223).
, а стерический фактор Р вычисляется по формуле (4.223). . (4.232)
. (4.232) . (4.233)
. (4.233) . (4.234)
. (4.234) . (4.235)
. (4.235) выражают через энергию Гельмгольца образования активированного комплекса:
выражают через энергию Гельмгольца образования активированного комплекса: =
=  . (4.236)
. (4.236) реагирует с двухвалентным железом по реакции:
реагирует с двухвалентным железом по реакции: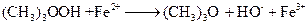 .
. =
=  =
= = 2,6·10-15см2.
= 2,6·10-15см2. . Откуда
. Откуда  = 38600 -0,5×8,314∙298= 37361,214 Дж/моль
= 38600 -0,5×8,314∙298= 37361,214 Дж/моль = 3,13∙10-7.
= 3,13∙10-7. [2] см3/(моль·с).
[2] см3/(моль·с). =
= =6,67 ×103
=6,67 ×103  .
. , где А оп – значение предэкспоненциального множителя в уравнении зависимости константы скорости от температуры
, где А оп – значение предэкспоненциального множителя в уравнении зависимости константы скорости от температуры  .
. л/(моль×с).
л/(моль×с). =
= = 2,046×1010 л/(моль×с).
= 2,046×1010 л/(моль×с). .
.
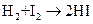
 ; б) энтропию активации
; б) энтропию активации  и
и  ; в) энергию Гиббса активации
; в) энергию Гиббса активации 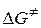 .
. =1.
=1. =1,79·105 л/моль·с
=1,79·105 л/моль·с ,
, =67443,308 Дж/моль.
=67443,308 Дж/моль. =
=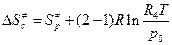 = -143,97 + 8,314
= -143,97 + 8,314  = - 110,43 Дж/моль.
= - 110,43 Дж/моль. = 67443,308 -689×(-110,43) = 143529,578 Дж/моль=143,53 кДж/моль.
= 67443,308 -689×(-110,43) = 143529,578 Дж/моль=143,53 кДж/моль. ;
;  = 1,55·10-11.
= 1,55·10-11. =12,2, вычислите при этой температуре энтальпию и энтропию активации реакции.
=12,2, вычислите при этой температуре энтальпию и энтропию активации реакции. , (5.1)
, (5.1) , (5.3)
, (5.3) – энтропия активации, т.е. энтропия образования активированного комплекса. Энтропия активации при образовании активированного комплекса из исходных веществ с участием катализатора, как правило, существенно уменьшается по сравнению с энтропией активации активированного комплекса в отсутствии катализатора, поскольку присутствие катализатора способствует большей упорядоченности в строении активированного комплекса. Имеются реакции, в которых катализатор почти не влияет на энергию активации, но сильно изменяет предэкспоненциальный множитель (А). Например, реакция гидролиза аденозинтрифосфорной кислоты (АТФ) в присутствии фермента (миозина) ускоряется по сравнению с действием ионов H3O+ в 1014 раз. Энергия активации процесса при этом практически не изменяется. Для реакции муторации глюкозы в присутствии различных катализаторов энергия активации так же практически не изменяется, предэкспоненциальный множитель(А) изменяется в 106 раз, а константа скорости от 106 до 107 раз. Но такого рода реакции всё-таки более редки.
– энтропия активации, т.е. энтропия образования активированного комплекса. Энтропия активации при образовании активированного комплекса из исходных веществ с участием катализатора, как правило, существенно уменьшается по сравнению с энтропией активации активированного комплекса в отсутствии катализатора, поскольку присутствие катализатора способствует большей упорядоченности в строении активированного комплекса. Имеются реакции, в которых катализатор почти не влияет на энергию активации, но сильно изменяет предэкспоненциальный множитель (А). Например, реакция гидролиза аденозинтрифосфорной кислоты (АТФ) в присутствии фермента (миозина) ускоряется по сравнению с действием ионов H3O+ в 1014 раз. Энергия активации процесса при этом практически не изменяется. Для реакции муторации глюкозы в присутствии различных катализаторов энергия активации так же практически не изменяется, предэкспоненциальный множитель(А) изменяется в 106 раз, а константа скорости от 106 до 107 раз. Но такого рода реакции всё-таки более редки. , где Т 1, = 298 К; Е 1 – энергия активации.
, где Т 1, = 298 К; Е 1 – энергия активации. ,
, , откуда
, откуда  .
. = 4 (дано по условию задачи), находим: Т 2= 4·298 = 1192 К (919 °С). Таким образом, для достижения одинаковой с каталитической реакцией скорости требуется значительное повышение температуры по сравнению с 298 К, т.е. существенные затраты энергии.[4]
= 4 (дано по условию задачи), находим: Т 2= 4·298 = 1192 К (919 °С). Таким образом, для достижения одинаковой с каталитической реакцией скорости требуется значительное повышение температуры по сравнению с 298 К, т.е. существенные затраты энергии.[4] , (1)
, (1)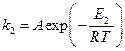 . (2)
. (2)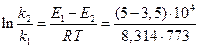 = 2,3; откуда
= 2,3; откуда  и
и  ;
; и
и  = 0.
= 0. , откуда
, откуда  =541,1 К(261,8) °С;
=541,1 К(261,8) °С; Ag2+ + Се3+, (1a)
Ag2+ + Се3+, (1a) Ag+ + Tl2+, (2)
Ag+ + Tl2+, (2)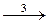 Tl3+ + Се3+, (3)
Tl3+ + Се3+, (3) (4)
(4) (5)
(5) (6)
(6) из выражения (6) в уравнение (4), получим
из выражения (6) в уравнение (4), получим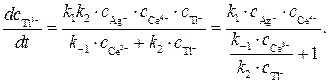 (7)
(7) в начальный период реакции таково, что в знаменателе никакой член не является доминирующим, это не позволяет провести аппроксимацию. Но на последних стадиях реакции первый член становится преобладающим, т.е. единицей можно пренебречь, и выражение для скорости аппроксимируется к виду
в начальный период реакции таково, что в знаменателе никакой член не является доминирующим, это не позволяет провести аппроксимацию. Но на последних стадиях реакции первый член становится преобладающим, т.е. единицей можно пренебречь, и выражение для скорости аппроксимируется к виду (8)
(8)


