Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Уравнение изотермы химической реакцииСодержание книги Поиск на нашем сайте
Уравнение изотермы химической реакции При протекании химической реакции через некоторое время устанавливается равновесное состояние, когда скорости прямой и обратной реакции равны. Пусть в смеси идеальных газов протекает химическая реакция: аА + вВ = eЕ + lL, где а, в, е и l – число моль газообразных веществ А, В, Е и L, принимающих участие в реакции или стехиометрические коэффициенты. Пусть в реакцию вступило бесконечно малое количество вещества А (dnA); с ним прореагировало бесконечно малое количество вещества В (dnB). В результате реакции образовалось dnE и dnL моль веществ С и D. Так как количество исходных веществ в ходе реакции убывает, а продуктов увеличивается, то величины dnA и dnB отрицательны, а dnE и dnL – положительны. Тогда изменение энергии Гиббса при протекании указанного процесса равно
Выразим количества моль прореагировавших веществ dnA, dnB, dnE, и dnL через стехиометрические коэффициенты уравнения реакции. Согласно уравнению реакции: с а моль вещества А реагирует в моль вещества В с dnA моль dnB, тогда
Аналогично можно выразить:
Подставим в уравнение для dG:
Умножим левую и правую часть уравнения на а и поделим на dnA:
Так как химический потенциал равен мольной энергии Гиббса
следовательно,
Химический потенциал компонента реакционной смеси равен
Подставим в уравнение
Обозначим сумму
Тогда
где Δ G0 – изменение энергии Гиббса в стандартных условиях; pE, pL, pA, pB – рабочие (неравновесные) парциальные давления компонентов в реакционной смеси. Уравнение (3.1) называется уравнением изотермы химической реакции, При постоянных давлении и температуре общим условием термодинамического равновесия является Δ G = 0. Тогда парциальные давления компонентов становятся равновесными
Введем обозначение:
где Кр – термодинамическая константа равновесия – величина постоянная для данной реакции при данной температуре. Термодинамическая константа равновесия является безразмерной величиной. Полученное уравнение (3.2) выражает известный закон действия масс: отношение произведения равновесных парциальных давлений продуктов реакции, взятых в степенях, равных стехиометрическим коэффициентам к аналогичному произведению для исходных веществ при данной температуре есть величина постоянная.
С учетом Кр получим
тогда константу равновесия реакции можно рассчитать по уравнению:
Кр не зависит от давления, так как связана с изменением энергии Гиббса в стандартных условиях, т.е. при р = 1 атм. Закон действия масс можно выразить не только через парциальные давления реагирующих веществ, но и через молярные концентрации (Кс) и мольные доли (Кх). Парциальное давление компонента системы связано с его молярной концентрацией и мольной долей уравнениями:
где xi – мольная доля i -го участника реакции; pобщ – общее давление реакционной смеси; сi – молярная концентрация i -го участника реакции. Тогда
Константы Кх связаны Кр соотношением
где Аналогично
Константа Kx зависит от общего давления реакционной смеси. Если реакция протекает в реальной системе, то вместо концентраций следует применять активности реагентов ai, а вместо парциальных давлений – фугитивности:
где γi – коэффициент активности;
γfi – коэффициент летучести. Если химическая реакция протекает с участием конденсированных веществ (твердых или жидких), то химический потенциал таких веществ зависит только от температуры и при Т = const является постоянной величиной. Поэтому парциальные давления конденсированных веществ постоянны и входят в значение Кр, а закон действия масс записывается только для газообразных участников реакции. Например, для реакции СаСО3(тв) = СаО(тв) + СО2(г) закон действия масс имеет вид
Значения констант равновесия многих химических реакций при 298 К приведены в справочной литературе. Основы формальной кинетики кинетика необратимых реакций Реакция нулевого порядка Это реакции, скорость которых не зависит от концентрации реагирующих веществ. Основной закон химической кинетики для реакции нулевого порядка записывается:
Разделим переменные и проинтегрируем в
где i – константа интегрирования. Если τ = 0, то
С учетом этого решим уравнение относительно k:
Зная константу скорости реакции, можно рассчитать концентрацию реагирующих веществ в любой момент времени:
Для характеристики скорости реакции применяется понятие времени полупревращения или полураспада τ1/2. Это есть время, за которое прореагирует половина взятого количества вещества. С учетом того, что
Время полупревращения реакции нулевого порядка прямо пропорционально концентрации исходного вещества. Реакция 1 порядка: А ® В. Пусть объем реакционной смеси равен V. Пусть в начальный момент времени τ = 0 в реакционной смеси содержится а моль вещества А и 0 моль вещества В. В момент времени τ в реакционной смеси а – х моль вещества А и х моль вещества В. Уравнение скорости химической реакции 1 порядка имеет вид
Концентрация вещества А равна
тогда
Подставим в уравнение и разделим переменные:
Из последнего уравнения следует, что скорость реакции 1 порядка не зависит от объема реакционной смеси. Проинтегрировав, получим
где i – константа интегрирования. При τ = 0 – х = 0, тогда
С учетом этого решим уравнение относительно k:
Разделив числитель и знаменатель на V, получим
Решим уравнение относительно
Время полупревращения реакции 1 порядка равно
Как видно, время полупревращения реакции 1 порядка не зависит от концентрации исходного вещества и обратно пропорционально константе скорости реакции. Реакция 2 порядка: A + B ® C + D. Пусть в объеме реакционной смеси V в начальный момент времени Запишем уравнение для скорости реакции
Текущие концентрации реагирующих веществ:
Производная от
тогда
Скорость реакции 2 порядка обратно пропорциональна объему реакционной смеси. Преобразуем уравнение:
Проинтегрируем в неопределенных пределах
При τ = 0 – х = 0, тогда
Подставим значение константы интегрирования и решим уравнение относительно k:
Поделим на V числитель и знаменатель правой части уравнения, а дробь, стоящую под знаком логарифма на V2, получим
где Полученное уравнение неприменимо для случая, когда
После интегрирования получим
При τ = 0 – х = 0, тогда
Подставим и решим уравнение относительно k:
Поделим на V2:
Текущую концентрацию вещества А можно рассчитать по формуле:
Время полупревращения вещества для реакции 2 порядка при a = b рассчитывается по уравнению:
5.3 Методы определения порядка реакции Из предыдущего раздела следует, что для создания математической модели химической реакции необходимо знать ее порядок. Существует несколько методов определения порядка реакции. 1. Метод подстановки. Сущность метода заключается в эмпирическом подборе такого кинетического уравнения, которое лучшим образом описывает результаты эксперимента. Существует два варианта реализации метода подстановки. 1) Аналитический метод, заключающийся в том, что для описания экспериментальных данных используются уравнения для реакций различных порядков и выбирается то уравнение, которое наилучшим образом описывает результаты эксперимента. Для этого по опытным значениям концентраций в различные моменты времени рассчитывают константу скорости реакции первого, второго и т.д. порядка. Уравнение удовлетворительно описывает процесс, если рассчитанные по нему значения констант колеблются около какой-либо средней величины и отклонения от среднего лежат в пределах погрешности определения.
2) Графический метод. Зависимость концентрации во времени для реакций различных порядков может быть выражена прямой линией, если подобрать соответствующую систему координат. Так для реакции нулевого порядка зависимость концентрации реагирующего вещества от времени имеет линейный вид:
Для реакции 1-го порядка прямая получается в системе координат lnС = f(t):
Для реакции 2-го порядка при
Подбирается случай, когда зависимость в соответствующих координатах прямолинейная. По тангенсу угла наклона можно определить значение константы скорости. Недостаток метода подстановки заключается в его трудоемкости. 2. Графический метод. Запишем кинетическое уравнение в виде:
прологарифмируем
Полученное уравнение является линейным, поэтому порядок реакции n будет равен тангенсу угла наклона прямой. Недостаток метода заключается в необходимости определения абсолютной скорости реакции, что может привести к ошибкам. 3. Метод Вант-Гоффа.
где ω 0² - скорость реакции при исходной концентрации реагирующего вещества с2; ω 0¢ - скорость реакции при исходной концентрации реагирующего вещества с1. Логарифмируя уравнения, почленно вычитая их друг из друга и решая относительно n, получим:
Метод Вант-Гоффа достаточно точен. 5. Метод избыточных концентраций (Оствальда). Основан на исследовании зависимости скорости реакции от начальной концентрации какого-либо одного реагента. Для этого в опытах меняется начальная концентрация одного реагента, а другие исходные вещества берутся в большом избытке – тогда концентрации этих веществ можно принять постоянными. Порядок по первому реагенту определяется по одному из вышеуказанных методов. Затем проводят аналогичные опыты с переменной начальной концентрацией другого исходного вещества в избытке остальных. Общий порядок реакции равен сумме порядков по отдельным компонентам.
Основные понятия катализа Катализ – явление ускорения реакций в присутствии веществ – катализаторов, которые присутствуют в реакционной смеси и увеличивают скорость реакции, но сами не претерпевают никаких изменений в результате ее протекания. Вещества, уменьшающие скорость реакции называются ингибиторами. Катализаторы не оказывают влияния на изменение энергии Гиббса и константу равновесия химической реакции, но могут сильно влиять на константу скорости реакции. Катализатор целесообразно применять для ускорения экзотермических реакций, так как повышение температуры при протекании таких реакций способствует смещению равновесия в сторону исходных веществ и уменьшению выхода продуктов реакции. Действие каждого катализатора специфично, то есть определенные катализаторы оказывают влияние лишь на некоторые реакции. Например, серебро ускоряет реакции окисления. Для ускорения реакции достаточно очень малого количества катализатора. Смесь катализаторов часто действует значительно сильнее по сравнению с действием отдельных катализаторов. При формальном подходе к каталитическим явлениям можно сказать, что механизм воздействия положительного катализатора заключается в снижении энергии активации реакции, а отрицательного – в увеличении. Различают гомогенный, гетерогенный и ферментативный катализ. При гомогенном катализе катализатор и реакционная смесь составляют одну фазу, а при гетерогенном – разные фазы. При ферментативном катализе катализаторами служат вещества белковой природы (ферменты). В основу гомогенного катализа положена теория промежуточного соединения, согласно которой катализатор образует с реагирующими веществами нестойкие промежуточные соединения, которые распадаются с образованием продуктов реакции и выделением катализатора в неизменном виде. Указанные процессы протекают быстрее, чем химическая реакция в отсутствии катализатора. На скорость гетерогенно-каталитического процесса сильно влияет площадь поверхности катализатора. Чем больше площадь поверхности, тем выше скорость процесса. Кроме того, на скорость гетерогенного катализа влияет состояние поверхности катализатора, а именно наличие активных центров – различного рода неоднородностей, обусловленных химическим составом, кристаллической структурой и т.д. Для создания активных центров на поверхности катализатора ее обрабатывают специальными веществами, который называются промоторами. При использовании катализатора его активность постепенно снижается. Вещества, снижающие активность катализатора называют каталитическими ядами.
Уравнение изотермы химической реакции При протекании химической реакции через некоторое время устанавливается равновесное состояние, когда скорости прямой и обратной реакции равны. Пусть в смеси идеальных газов протекает химическая реакция: аА + вВ = eЕ + lL, где а, в, е и l – число моль газообразных веществ А, В, Е и L, принимающих участие в реакции или стехиометрические коэффициенты.
Пусть в реакцию вступило бесконечно малое количество вещества А (dnA); с ним прореагировало бесконечно малое количество вещества В (dnB). В результате реакции образовалось dnE и dnL моль веществ С и D. Так как количество исходных веществ в ходе реакции убывает, а продуктов увеличивается, то величины dnA и dnB отрицательны, а dnE и dnL – положительны. Тогда изменение энергии Гиббса при протекании указанного процесса равно
Выразим количества моль прореагировавших веществ dnA, dnB, dnE, и dnL через стехиометрические коэффициенты уравнения реакции. Согласно уравнению реакции: с а моль вещества А реагирует в моль вещества В с dnA моль dnB, тогда
Аналогично можно выразить:
Подставим в уравнение для dG:
Умножим левую и правую часть уравнения на а и поделим на dnA:
Так как химический потенциал равен мольной энергии Гиббса
следовательно,
Химический потенциал компонента реакционной смеси равен
Подставим в уравнение
Обозначим сумму
Тогда
где Δ G0 – изменение энергии Гиббса в стандартных условиях; pE, pL, pA, pB – рабочие (неравновесные) парциальные давления компонентов в реакционной смеси. Уравнение (3.1) называется уравнением изотермы химической реакции, При постоянных давлении и температуре общим условием термодинамического равновесия является Δ G = 0. Тогда парциальные давления компонентов становятся равновесными
Введем обозначение:
где Кр – термодинамическая константа равновесия – величина постоянная для данной реакции при данной температуре. Термодинамическая константа равновесия является безразмерной величиной. Полученное уравнение (3.2) выражает известный закон действия масс: отношение произведения равновесных парциальных давлений продуктов реакции, взятых в степенях, равных стехиометрическим коэффициентам к аналогичному произведению для исходных веществ при данной температуре есть величина постоянная. С учетом Кр получим
тогда константу равновесия реакции можно рассчитать по уравнению:
Кр не зависит от давления, так как связана с изменением энергии Гиббса в стандартных условиях, т.е. при р = 1 атм. Закон действия масс можно выразить не только через парциальные давления реагирующих веществ, но и через молярные концентрации (Кс) и мольные доли (Кх). Парциальное давление компонента системы связано с его молярной концентрацией и мольной долей уравнениями:
где xi – мольная доля i -го участника реакции; pобщ – общее давление реакционной смеси; сi – молярная концентрация i -го участника реакции. Тогда
Константы Кх связаны Кр соотношением
где Аналогично
Константа Kx зависит от общего давления реакционной смеси. Если реакция протекает в реальной системе, то вместо концентраций следует применять активности реагентов ai, а вместо парциальных давлений – фугитивности:
где γi – коэффициент активности;
γfi – коэффициент летучести. Если химическая реакция протекает с участием конденсированных веществ (твердых или жидких), то химический потенциал таких веществ зависит только от температуры и при Т = const является постоянной величиной. Поэтому парциальные давления конденсированных веществ постоянны и входят в значение Кр, а закон действия масс записывается только для газообразных участников реакции. Например, для реакции СаСО3(тв) = СаО(тв) + СО2(г) закон действия масс имеет вид
Значения констант равновесия многих химических реакций при 298 К приведены в справочной литературе.
|
|||||||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 203; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.105.199 (0.017 с.) |

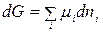
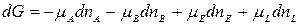
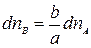 .
.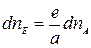 ;
;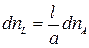
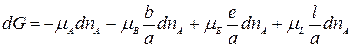 .
.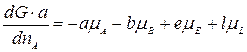
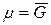 , то
, то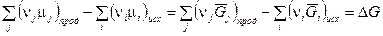 ,
,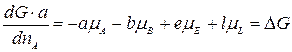
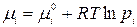 .
.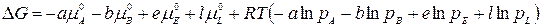
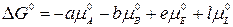 ,
,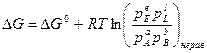 . (3.1)
. (3.1)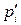 и из уравнения (3.1) следует, что
и из уравнения (3.1) следует, что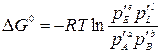 .
.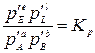 , (3.2)
, (3.2)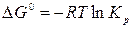 ,
,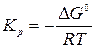 .
.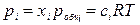 ,
,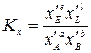 ;
;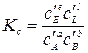
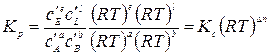 ,
,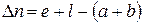
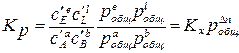
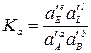 ;
;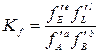 ,
,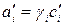 - активность i-го участника реакции;
- активность i-го участника реакции;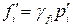 - фугитивность (летучесть) i-го участника реакции;
- фугитивность (летучесть) i-го участника реакции;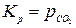 .
.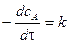
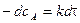 ,
,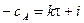 ,
,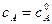 – начальная концентрация вещества А в момент времени
– начальная концентрация вещества А в момент времени 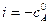
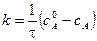 .
.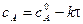
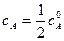 получим
получим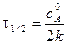
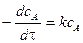 .
.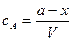 ,
,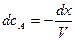 .
.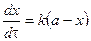 ,
,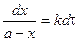 .
.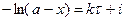 ,
,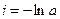
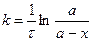 .
.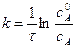 ,
,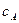 :
: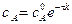 .
.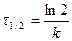 .
.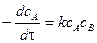
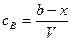 .
.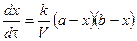 .
.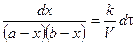 (*);
(*);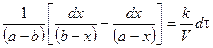
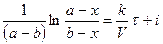 .
.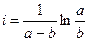
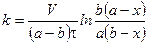
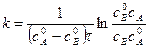 ,
,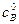 – исходная концентрация вещества В.
– исходная концентрация вещества В.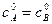 . Рассмотрим этот случай. Если a = b, то уравнение (*) запишется в виде:
. Рассмотрим этот случай. Если a = b, то уравнение (*) запишется в виде: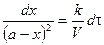
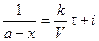
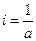 .
.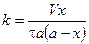 .
.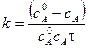 .
.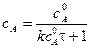 .
.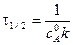 .
.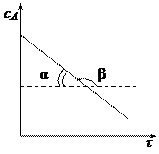
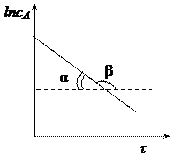
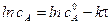
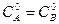 линейная зависимость в координатах
линейная зависимость в координатах 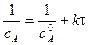

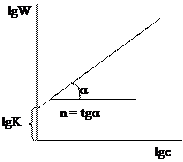
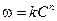 ,
,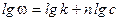 .
.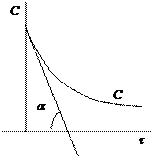 Основан на определении абсолютной скорости реакции в начальный момент времени при двух различных концентрациях реагирующего вещества:
Основан на определении абсолютной скорости реакции в начальный момент времени при двух различных концентрациях реагирующего вещества: 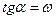 . Тогда:
. Тогда: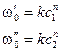 ,
,