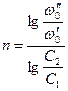Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Основной закон химической кинетики.Содержание книги Поиск на нашем сайте
Порядок и молекулярность реакции Реакция, протекающая в результате прямого превращения молекул исходных веществ в молекулы продуктов реакции, называется элементарной. Элементарная реакция состоит из большого числа однотипных элементарных актов химического превращения. Число молекул, участвующих в элементарном акте химического превращения, называется молекулярностью реакции. Молекулярность реакции – всегда целое положительное число: 1, 2 и реже 3. Элементарных химических актов с одновременным участием четырех молекул не бывает, так как вероятность одновременного столкновения четырех молекул ничтожно мала. Для мономолекулярной реакции скорость пропорциональна числу реагирующих молекул в единице объема, то есть концентрации вещества. Для би- и тримолекулярных реакций скорость пропорциональна произведению концентраций реагирующих веществ. На основе приведенных рассуждений сформулирован основной закон химической кинетики или закон действия масс: Скорость элементарной химической реакции прямо пропорциональна произведению концентраций молекул реагирующих веществ в степенях, равных стехиометрическим коэффициентам в уравнении реакции. Если реакция (*) выражает элементарный акт химического взаимодействия, то скорость реакции можно выразить:
где k – константа скорости реакции. Константа скорости имеет смысл удельной скорости химической реакции, то есть скорости при концентрациях реагирующих веществ, равных 1. Константа скорости химической реакции не зависит от концентрации реагирующих веществ, а определяется только природой этих веществ, характером химического превращения и температурой процесса. Сумма стехиометрических коэффициентов Большинство химических реакций являются сложными и включают несколько элементарных стадий химического превращения, каждая из которых может быть моно-, би- или тримолекулярной. Стадии могут сильно различаться по своим скоростям. Самая медленная стадия химической реакции определяет скорость процесса и называется лимитирующей. Лимитирующая стадия может быть одна, а в некоторых случаях таких стадий может быть несколько, когда две или более стадий протекают с одинаковыми скоростями. Если механизм реакции не изучен и лимитирующая стадия не выявлена, то закон действия масс не может быть использован для описания химического превращения в целом. Однако часто закон действующих масс формально применяется для описания скорости сложных реакции. Если уравнение (*) отражает протекание сложной реакции, то ее скорость можно выразить:
где n1, n2 – эмпирические коэффициенты, которые называются частными порядками химической реакции. Сумма частных порядков Основы формальной кинетики кинетика необратимых реакций Реакция нулевого порядка Это реакции, скорость которых не зависит от концентрации реагирующих веществ. Основной закон химической кинетики для реакции нулевого порядка записывается:
Разделим переменные и проинтегрируем в
где i – константа интегрирования. Если τ = 0, то
С учетом этого решим уравнение относительно k:
Зная константу скорости реакции, можно рассчитать концентрацию реагирующих веществ в любой момент времени:
Для характеристики скорости реакции применяется понятие времени полупревращения или полураспада τ1/2. Это есть время, за которое прореагирует половина взятого количества вещества. С учетом того, что
Время полупревращения реакции нулевого порядка прямо пропорционально концентрации исходного вещества. Реакция 1 порядка: А ® В. Пусть объем реакционной смеси равен V. Пусть в начальный момент времени τ = 0 в реакционной смеси содержится а моль вещества А и 0 моль вещества В. В момент времени τ в реакционной смеси а – х моль вещества А и х моль вещества В. Уравнение скорости химической реакции 1 порядка имеет вид
Концентрация вещества А равна
тогда
Подставим в уравнение и разделим переменные:
Из последнего уравнения следует, что скорость реакции 1 порядка не зависит от объема реакционной смеси. Проинтегрировав, получим
где i – константа интегрирования. При τ = 0 – х = 0, тогда
С учетом этого решим уравнение относительно k:
Разделив числитель и знаменатель на V, получим
Решим уравнение относительно
Время полупревращения реакции 1 порядка равно
Как видно, время полупревращения реакции 1 порядка не зависит от концентрации исходного вещества и обратно пропорционально константе скорости реакции. Реакция 2 порядка: A + B ® C + D. Пусть в объеме реакционной смеси V в начальный момент времени Запишем уравнение для скорости реакции
Текущие концентрации реагирующих веществ:
Производная от
тогда
Скорость реакции 2 порядка обратно пропорциональна объему реакционной смеси. Преобразуем уравнение:
Проинтегрируем в неопределенных пределах
При τ = 0 – х = 0, тогда
Подставим значение константы интегрирования и решим уравнение относительно k:
Поделим на V числитель и знаменатель правой части уравнения, а дробь, стоящую под знаком логарифма на V2, получим
где Полученное уравнение неприменимо для случая, когда
После интегрирования получим
При τ = 0 – х = 0, тогда
Подставим и решим уравнение относительно k:
Поделим на V2:
Текущую концентрацию вещества А можно рассчитать по формуле:
Время полупревращения вещества для реакции 2 порядка при a = b рассчитывается по уравнению:
5.3 Методы определения порядка реакции Из предыдущего раздела следует, что для создания математической модели химической реакции необходимо знать ее порядок. Существует несколько методов определения порядка реакции. 1. Метод подстановки. Сущность метода заключается в эмпирическом подборе такого кинетического уравнения, которое лучшим образом описывает результаты эксперимента. Существует два варианта реализации метода подстановки. 1) Аналитический метод, заключающийся в том, что для описания экспериментальных данных используются уравнения для реакций различных порядков и выбирается то уравнение, которое наилучшим образом описывает результаты эксперимента. Для этого по опытным значениям концентраций в различные моменты времени рассчитывают константу скорости реакции первого, второго и т.д. порядка. Уравнение удовлетворительно описывает процесс, если рассчитанные по нему значения констант колеблются около какой-либо средней величины и отклонения от среднего лежат в пределах погрешности определения. 2) Графический метод. Зависимость концентрации во времени для реакций различных порядков может быть выражена прямой линией, если подобрать соответствующую систему координат. Так для реакции нулевого порядка зависимость концентрации реагирующего вещества от времени имеет линейный вид:
Для реакции 1-го порядка прямая получается в системе координат lnС = f(t):
Для реакции 2-го порядка при
Подбирается случай, когда зависимость в соответствующих координатах прямолинейная. По тангенсу угла наклона можно определить значение константы скорости. Недостаток метода подстановки заключается в его трудоемкости. 2. Графический метод. Запишем кинетическое уравнение в виде:
прологарифмируем
Полученное уравнение является линейным, поэтому порядок реакции n будет равен тангенсу угла наклона прямой. Недостаток метода заключается в необходимости определения абсолютной скорости реакции, что может привести к ошибкам. 3. Метод Вант-Гоффа.
где ω 0² - скорость реакции при исходной концентрации реагирующего вещества с2; ω 0¢ - скорость реакции при исходной концентрации реагирующего вещества с1. Логарифмируя уравнения, почленно вычитая их друг из друга и решая относительно n, получим:
Метод Вант-Гоффа достаточно точен. 5. Метод избыточных концентраций (Оствальда). Основан на исследовании зависимости скорости реакции от начальной концентрации какого-либо одного реагента. Для этого в опытах меняется начальная концентрация одного реагента, а другие исходные вещества берутся в большом избытке – тогда концентрации этих веществ можно принять постоянными. Порядок по первому реагенту определяется по одному из вышеуказанных методов. Затем проводят аналогичные опыты с переменной начальной концентрацией другого исходного вещества в избытке остальных. Общий порядок реакции равен сумме порядков по отдельным компонентам.
|
||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 604; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.41 (0.006 с.) |

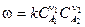 ,
,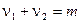 – молекулярность химической реакции.
– молекулярность химической реакции.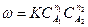
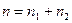 – называется порядком химической реакции. Частные порядки реакции в общем случае не равны стехиометрическим коэффициентам и могут совпадать с ними лишь для элементарных реакций. Частные порядки и общий порядок реакции определяются только экспериментально. Порядок реакции может принимать значения целые дробные, даже отрицательные и может быть равен нулю.
– называется порядком химической реакции. Частные порядки реакции в общем случае не равны стехиометрическим коэффициентам и могут совпадать с ними лишь для элементарных реакций. Частные порядки и общий порядок реакции определяются только экспериментально. Порядок реакции может принимать значения целые дробные, даже отрицательные и может быть равен нулю.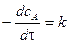
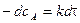 ,
,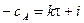 ,
,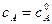 – начальная концентрация вещества А в момент времени
– начальная концентрация вещества А в момент времени 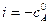
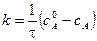 .
.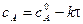
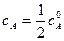 получим
получим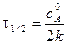
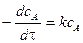 .
.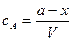 ,
,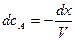 .
.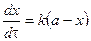 ,
,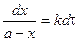 .
.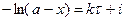 ,
,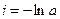
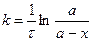 .
.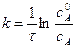 ,
,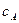 :
: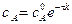 .
.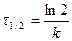 .
.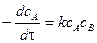
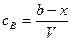 .
.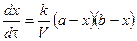 .
.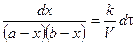 (*);
(*);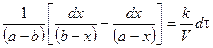
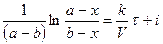 .
.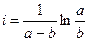
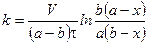
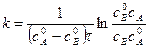 ,
,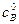 – исходная концентрация вещества В.
– исходная концентрация вещества В.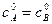 . Рассмотрим этот случай. Если a = b, то уравнение (*) запишется в виде:
. Рассмотрим этот случай. Если a = b, то уравнение (*) запишется в виде: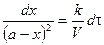
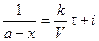
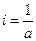 .
.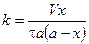 .
.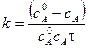 .
.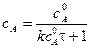 .
.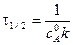 .
.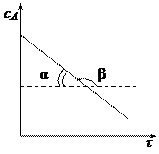
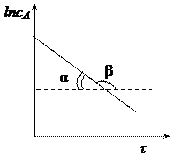
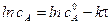
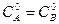 линейная зависимость в координатах
линейная зависимость в координатах 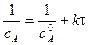

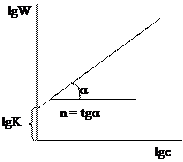
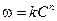 ,
,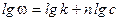 .
.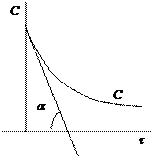 Основан на определении абсолютной скорости реакции в начальный момент времени при двух различных концентрациях реагирующего вещества:
Основан на определении абсолютной скорости реакции в начальный момент времени при двух различных концентрациях реагирующего вещества: 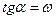 . Тогда:
. Тогда: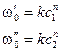 ,
,