
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Работа 4. Измерение скорости полета пули с помощью баллистического маятникаСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Цель работы - определить скорость полета пули с помощью крутильных колебаний баллистического маятника.
Теоретические основы лабораторной работы
Скорость полета пули может достигать значительной величины в зависимости от стреляющего устройства. Ее прямое измерение, то есть определение времени, за которое пуля проходит известное расстояние, в учебной лаборатории не представляется возможным. Для лабораторной работы разработана методика косвенного измерения скорости полета пули с помощью баллистического маятника. В основе эксперимента лежит явление неупругого соударения тел, в результате которого баллистический маятник совершает крутильные колебания. Если летящая пуля испытывает неупругий удар с неподвижным телом большей массы, то скорость тела после удара будет существенно меньше первоначальной скорости пули и ее можно будет измерить достаточно простыми методами.
При выводе расчётных формул использованы формулы для момента инерции и периода крутильных колебаний физического маятника, а также законы сохранения момента импульса и полной механической энергии. Принято допущение при этом о малости неконсервативных сил. На основании закона сохранения момента импульса можно написать
где m - масса пули; u - величина скорости пули; l - расстояние от оси вращения маятника до точки удара пули; w - величина угловой скорости маятника; J - момент инерции маятника. Согласно закону сохранения полной механической энергии при повороте маятника кинетическая энергия маятника переходит в потенциальную энергию закручивающейся проволоки
где Учитывая, что момент инерции пули
Модуль кручения проволоки D можно определить, измерив период крутильных колебаний маятника Т. При малых углах отклонения период крутильных колебаний маятника определяется по формуле
Модуль кручения проволоки
Подставив выражение (4.5) в уравнение (4.3), выразим величину скорости пули
Чтобы исключить измерения момента инерции J, запишем периоды колебаний маятника Т 1 и Т 2 при различных положениях грузов R 1 и R 2:
отсюда
В силу того, что момент инерции величина аддитивная, момент инерции баллистического маятника с грузами выразим в виде суммы
где М - масса двух неподвижных грузов; R - расстояние от центра масс груза до оси вращения; J 0 - момент инерции маятника без грузов. Для различных положений грузов на расстояниях R1 и R2: в первом положении
Разность моментов инерции
Решая уравнение (8) и (10) относительно J1 найдем
Подставив в формулу (4.6) период T1 и момент инерции J1 для положения грузов на расстоянии R1, получим окончательную формулу для расчета величины скорости пули
Описание установки
Порядок выполнения работы
Таблица 4.1.
Обработка результатов измерений
Контрольные вопросы 1. Что такое баллистический маятник? 2. От каких параметров установки зависит период колебаний баллистического маятника? 3. От чего зависит амплитуда колебаний баллистического маятника? 4. Что называется периодом колебаний? 5. Что характеризует вектор скорости? 6. Что характеризует модуль скорости? 7.При каких допущениях получена формула для величины скорости? 8. Какие законы и соотношения использованы при выводе расчётной формулы для вычисления величины скорости? 9. Какой удар называется неупругим? 10. Можно ли пользоваться формулой (4.12), если удар пули о мишень происходит под углом, отличным от прямого угла?
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-08; просмотров: 896; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.62 (0.008 с.) |

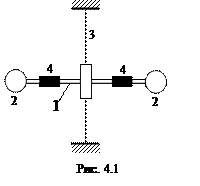 Баллистический маятник представляет собой два стержня 1, подвешенных на вертикально натянутой проволоке 3 (рис. 4.1). На стержнях закреплены мисочки с пластилином 2 и перемещаемые грузы 4. При попадании пули в мисочку с пластилином, маятник начинает поворачиваться вокруг своей вертикальной оси, совершая крутильные колебания.
Баллистический маятник представляет собой два стержня 1, подвешенных на вертикально натянутой проволоке 3 (рис. 4.1). На стержнях закреплены мисочки с пластилином 2 и перемещаемые грузы 4. При попадании пули в мисочку с пластилином, маятник начинает поворачиваться вокруг своей вертикальной оси, совершая крутильные колебания. , (4.1)
, (4.1) , (4.2)
, (4.2) - наибольший угол поворота маятника; D - модуль кручения проволоки.
- наибольший угол поворота маятника; D - модуль кручения проволоки. существенно меньше момента инерции маятника J, из уравнений (1) и (2) получим
существенно меньше момента инерции маятника J, из уравнений (1) и (2) получим . (4.3)
. (4.3) (4.4)
(4.4)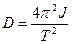 (4.5)
(4.5) =
=  (4.6)
(4.6)
 (4.7)
(4.7) (4.8)
(4.8) (4.9)
(4.9) ; во втором положении
; во втором положении
 (4.10)
(4.10) (4.11)
(4.11) . (12)
. (12) Общий вид установки показан на рис. 4.2. В основании 1, снабженном регулирующими ножками 2, позволяющими выравнивать прибор, закреплена колонка 3 с тремя кронштейнами: верхним 8, средним 4 и нижним 14. К кронштейну 4 прикреплено стреляющее устройство 9, прозрачный экран с нанесенной на него угловой шкалой 10 и фотоэлектрический датчик 12. Кронштейны 4 и 8 имеют зажимы, служащие для крепления стальной проволоки 13, на которой подвешен маятник, состоящий из двух мисочек 6, наполненных пластилином, двух перемещаемых грузов 7, двух стержней 5 и «водилки» 11. Фотоэлектрический датчик соединен разъёмом с привинченным к основанию секундомером.
Общий вид установки показан на рис. 4.2. В основании 1, снабженном регулирующими ножками 2, позволяющими выравнивать прибор, закреплена колонка 3 с тремя кронштейнами: верхним 8, средним 4 и нижним 14. К кронштейну 4 прикреплено стреляющее устройство 9, прозрачный экран с нанесенной на него угловой шкалой 10 и фотоэлектрический датчик 12. Кронштейны 4 и 8 имеют зажимы, служащие для крепления стальной проволоки 13, на которой подвешен маятник, состоящий из двух мисочек 6, наполненных пластилином, двух перемещаемых грузов 7, двух стержней 5 и «водилки» 11. Фотоэлектрический датчик соединен разъёмом с привинченным к основанию секундомером. по результатам измерения αmax.
по результатам измерения αmax. .
.


