
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Элементарная теория оценки ошибок измеренийСодержание книги
Поиск на нашем сайте Методическое пособие
для выполнения лабораторных работ по физике
часть I
Ф.И.О. студента___________________________________________
№ группы ________________________________________________
УКП ____________________________________________________
Ф.И.О. ведущего преподавателя _____________________________ _________________________________________________________
Лаб. работа №101 РАБОТА ЗАЧТЕНА
Лаб. работа №102 РАБОТА ЗАЧТЕНА
Лаб. работа №106 РАБОТА ЗАЧТЕНА
___________________________
Порядок выполнения работ 1. Лабораторные работы предназначены для проверки изучаемых физических законов на практике. 2. Номер работы, которую студент будет выполнять на следующем занятии, назначает преподаватель, проводящий лабораторные работы. 3. Экспериментальные и расчетные данные заносятся в журнал только с разрешения ведущего преподавателя. Все предварительные расчеты выполняются на черновике. Обработка результатов измерений проводится согласно разделу «Элементарная теория оценки ошибок измерения» (cм. ниже). 4. После выполнения работы преподаватель должен поставить отметку в журнале о том, что работа зачтена. 5. Студенты, не сдавшие в срок лабораторные работы, к экзамену не допускаются.
ЭЛЕМЕНТАРНАЯ ТЕОРИЯ ОЦЕНКИ ОШИБОК ИЗМЕРЕНИЙ Целью каждой лабораторной работы является определение некоторой величины y, для которой приводится функциональное соотношение (формула), выражающая ее через одну или несколько величин
Непосредственно в эксперименте измеряется не сама искомая величина у, а только величины x 1, х 2,..., хN, которые в дальнейшем называются измерениями. Для измерения величин Поэтому любую из измеряемых на практике физических величин можно представить в виде Будем считать, что все отклонения истинного значения чему соответствует форма записи результатов измерений в виде Величина 1) значение абсолютной ошибки 2) при записи численного значения величины хСР необходимо указывать столько же знаков после запятой, сколько использовано для записи 1) 2) Примеры неправильной записи результата измерений: 1) х = (1.11 ± 0.01) м – нарушено правило 1; 2) х = (1.11 ± 0.013) м – нарушено правило 2; 3) х = (1.11 ± 0.0134) м – нарушено правило 1; 4) х = (1.11 ± 0.023) м – нарушено правило 1. Класс точности измерений характеризуется как величиной абсолютных ошибок, так и относительных, которые вычисляются по формуле: Относительная ошибка во многом более наглядна. Например, измерения размеров дома и земного шара с точностью до одного метра совершенно несоизмеримы по величине относительных ошибок, отличающихся почти в миллион раз.
ЛАБОРАТОРНАЯ РАБОТА №101 Проведение эксперимента а) ускоренное движение 1. Включить тумблер «СЕТЬ». 2. Определить длину участка движения грузов h с помощью линейки 3 по уровню кронштейна 4. Записать h, а также массу цилиндра и перегрузка типа А D М 1 в табл. 1. 3. Сбросить показания индикатора 10 (нажать кнопку «СБРОС». При этом тормоз будет автоматически включен). 4. Поместить перегрузок типа А D М 1 на правый цилиндр 6. 5. Поднять правый груз до кронштейна 4 так, чтобы середина цилиндра была на уровне кронштейна. 6. Нажать клавишу "ПУСК". 7. С индикатора 10 снять показание времени t движения грузов на участке h. Занести значение t в табл. 1. 8. Сбросить показания индикатора 10 кнопкой «СБРОС». 9. Эксперимент повторять, начиная с п.2, по три раза каждым из перегрузков типа А (D М 1, D М 2 и D М 3). Таблица 1.
И ИМПУЛЬСА НА ПРИМЕРЕ ЦЕНТРАЛЬНОГО УДАРА ШАРОВ 1. Цель работы: Экспериментальная проверка законов сохранения механической энергии и импульса при центральном ударе шаров; определение коэффициента восстановления; определение величины потери энергии при центральном ударе шаров. 2. Теоретическая часть Удар называется центральным, если шары до удара движутся вдоль прямой, проходящей через их центры. Существуют два предельных вида ударов: абсолютно упругий удар и абсолютно неупругий удар, которые в чистом виде для макротел не реализуются. Абсолютно упругим ударом называется такой удар, при котором механическая энергия не переходит в другие виды энергии. При таком ударе кинетическая энергия полностью переходит в потенциальную энергию упругой деформации. Затем тела принимают первоначальную форму, отталкиваясь друг от друга. Потенциальная энергия упругой деформации вновь полностью переходит в кинетическую. При абсолютно упругом ударе выполняются закон сохранения импульса и закон сохранения механической энергии.
где При центральном ударе скорости шаров после удара будут направлены вдоль той же прямой, вдоль которой двигались центры до удара. Решая систему (1, 2), определяем скорости шаров после удара:
Для численных расчетов нужно спроецировать соотношение (3) на ось, вдоль которой движутся шары. Абсолютно неупругий удар характеризуется тем, что потенциальной энергии деформации не возникает, и кинетическая энергия полностью или частично превращается во внутреннюю энергию. После удара тела движутся с одинаковой скоростью либо покоятся. При абсолютно неупругом ударе не выполняется закон сохранения механической энергии, выполняется только закон сохранения импульса:
Отсюда получаем скорость шаров после удара При абсолютно неупругом ударе кинетическая энергия частично превращается в другие немеханические виды энергии (например, во внутреннюю энергию, что приводит к нагреванию соударяющихся тел). Следовательно, потеря кинетической энергии равна разности между начальным и конечным ее значениями. С учетом (5) получим
Потери энергии при неупругом ударе можно определить по формуле (
Мерой неупругости удара служит коэффициент восстановления К, численно равный отношению относительной скорости шаров после удара к относительной скорости до удара При абсолютно упругом ударе К = 1, при абсолютно неупругом К = 0. 3. Экспериментальная часть Порядок выполнения работы Определение углов отклонения: 1) установить шары массой m 1 и m 2 в положение равновесия; 2) нажать кнопку 7 «СЕТЬ». При этом включается электромагнит 2; 3) отклонить шар m 1 на угол j10 до касания с электромагнитом 2; при этом шар m 1 зафиксируется в неподвижном положении; 4) нажать кнопку 8 «ПУСК» и зафиксировать угол отклонения j2 шара m 2 и угол отклонения j1 шара m1 после удара; 5) для выбранного угла j10 провести измерения не менее 7 раз. Результаты измерений углов j1 и j2 занести в табл. 1. Таблица 1.
Порядок выполнения работы 1. Определение момента инерции и углового ускорения. 1) наматывая нить на шкив, поднять груз на определенную высоту h. Записать высоту поднятия груза h и радиус шкива R в табл. 1; 2) расположить грузы m 0 на одинаковом расстоянии от оси вращения крестовины (например, на концах осей маятника Обербека); 3) измерить три раза время падения груза с одной массой m. Занести данные в табл. 1; 4) опыт проделать три раза с различными массами груза т. Занести данные в табл. 1. Таблица 1
2. Исследование зависимости e и JZ от расположения масс на крестовине маятника. Проделать предыдущий опыт для различных положений грузов m 0 на осях крестовины (размещая грузы симметрично у основания крестовины, в середине и по краям). Массу груза m не изменять. Результаты занести в табл. 2. Таблица 2
Методическое пособие
для выполнения лабораторных работ по физике
часть I
Ф.И.О. студента___________________________________________
№ группы ________________________________________________
УКП ____________________________________________________
Ф.И.О. ведущего преподавателя _____________________________ _________________________________________________________
Лаб. работа №101 РАБОТА ЗАЧТЕНА
Лаб. работа №102 РАБОТА ЗАЧТЕНА
Лаб. работа №106 РАБОТА ЗАЧТЕНА
___________________________
Порядок выполнения работ 1. Лабораторные работы предназначены для проверки изучаемых физических законов на практике. 2. Номер работы, которую студент будет выполнять на следующем занятии, назначает преподаватель, проводящий лабораторные работы. 3. Экспериментальные и расчетные данные заносятся в журнал только с разрешения ведущего преподавателя. Все предварительные расчеты выполняются на черновике. Обработка результатов измерений проводится согласно разделу «Элементарная теория оценки ошибок измерения» (cм. ниже). 4. После выполнения работы преподаватель должен поставить отметку в журнале о том, что работа зачтена. 5. Студенты, не сдавшие в срок лабораторные работы, к экзамену не допускаются.
ЭЛЕМЕНТАРНАЯ ТЕОРИЯ ОЦЕНКИ ОШИБОК ИЗМЕРЕНИЙ Целью каждой лабораторной работы является определение некоторой величины y, для которой приводится функциональное соотношение (формула), выражающая ее через одну или несколько величин
Непосредственно в эксперименте измеряется не сама искомая величина у, а только величины x 1, х 2,..., хN, которые в дальнейшем называются измерениями. Для измерения величин Поэтому любую из измеряемых на практике физических величин можно представить в виде Будем считать, что все отклонения истинного значения чему соответствует форма записи результатов измерений в виде Величина 1) значение абсолютной ошибки 2) при записи численного значения величины хСР необходимо указывать столько же знаков после запятой, сколько использовано для записи 1) 2) Примеры неправильной записи результата измерений: 1) х = (1.11 ± 0.01) м – нарушено правило 1; 2) х = (1.11 ± 0.013) м – нарушено правило 2; 3) х = (1.11 ± 0.0134) м – нарушено правило 1; 4) х = (1.11 ± 0.023) м – нарушено правило 1. Класс точности измерений характеризуется как величиной абсолютных ошибок, так и относительных, которые вычисляются по формуле: Относительная ошибка во многом более наглядна. Например, измерения размеров дома и земного шара с точностью до одного метра совершенно несоизмеримы по величине относительных ошибок, отличающихся почти в миллион раз.
ЛАБОРАТОРНАЯ РАБОТА №101
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 275; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.62 (0.01 с.) |

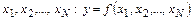 . (1)
. (1) используются приборы, реальные измерительные возможности которых ограничиваются рядом объективных причин, кроющихся в физической природе измеряемых физических величин. Так при измерении плотности с высокой точностью проявляются флуктуации числа частиц и массы в единице объема. При измерении тока – числа носителей заряда, при измерении интенсивности света – числа фотонов в световых потоках и многое другое.
используются приборы, реальные измерительные возможности которых ограничиваются рядом объективных причин, кроющихся в физической природе измеряемых физических величин. Так при измерении плотности с высокой точностью проявляются флуктуации числа частиц и массы в единице объема. При измерении тока – числа носителей заряда, при измерении интенсивности света – числа фотонов в световых потоках и многое другое. , где
, где  – некоторое истинное точное значение (которое полагается физически существующим) измеряемой величины, а D х – отклонение от истинного значения, обусловленное неточностями лабораторного эксперимента.
– некоторое истинное точное значение (которое полагается физически существующим) измеряемой величины, а D х – отклонение от истинного значения, обусловленное неточностями лабораторного эксперимента. ,
, , где xCP – среднее значение измеряемой величины х. Оно определяется, как среднее арифметическое по всем измерениям:
, где xCP – среднее значение измеряемой величины х. Оно определяется, как среднее арифметическое по всем измерениям:  , где хi – значение величины х в i -том измерении; n – полное количество измерений.
, где хi – значение величины х в i -том измерении; n – полное количество измерений. называется средней абсолютной ошибкой измеряемой величины х. Она определяется, как
называется средней абсолютной ошибкой измеряемой величины х. Она определяется, как  где вертикальными скобками обозначен модуль разности. При записи результата измерений необходимо соблюдать следующие правила:
где вертикальными скобками обозначен модуль разности. При записи результата измерений необходимо соблюдать следующие правила: , если
, если  , а
, а  ;
; , если
, если  , а
, а  .
. , (1)
, (1) , (2)
, (2)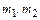 – массы шаров;
– массы шаров; 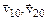 – скорости шаров до удара;
– скорости шаров до удара;  – скорости шаров после удара.
– скорости шаров после удара. ,
,  . (3)
. (3) . (4)
. (4) . (5)
. (5) . (6)
. (6) Неупругий удар представляет собой промежуточный случай между абсолютно упругим и абсолютно неупругим ударом.
Неупругий удар представляет собой промежуточный случай между абсолютно упругим и абсолютно неупругим ударом.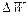 – величина потери энергии):
– величина потери энергии): . (7)
. (7) . (8)
. (8) рад/с2
рад/с2



