
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Изучение основного закона динамики вращательного движения твердого телаСодержание книги
Поиск на нашем сайте
1. Цель работы: проверка основного закона вращательного движения твердого тела. Экспериментальная проверка зависимости углового ускорения тела от величины момента внешних сил и зависимости момента инерции тела от распределения масс. 2. Теоретическая часть: при вращательном движении, кроме массы и сил, действующих на тело, вводятся физические величины, зависящие от точки приложения силы и от распределения массы тела. Такими величинами являются момент сил и момент инерции. Момент силы относительно точки О определяется по формуле:
Момент инерции – физическая величина, характеризующая распределение масс тела и являющаяся мерой инертности вращающегося тела. В общем случае момент инерции можно найти по формуле: где dm и dV – элементарные массы и объем, r – кратчайшее расстояние от оси вращения до выбранной элементарной массы, r = dm/dV – плотность тела в данной точке. Момент инерции маятника Обербека относительно оси вращения Z, перпендикулярной плоскости рисунка(рис. 1), равен сумме моментов инерции четырех грузов массы т 0и четырех стержней массы тст где r – расстояние от оси вращения до центра груза т 0. Момент силы
Для экспериментального определения MZ, JZ, e и проверки уравнения (4) удобно использовать крестообразный маятник (маятник Обербека) (рис. 1). Вращение маятника Обербека создается за счет груза массой m, движущегося поступательно вертикально вниз. По второму закону Ньютона где В проекциях на ось X На крестообразный маятник действует, согласно третьему закону Ньютона, сила где R – радиус шкива. Основное уравнение динамики вращательного движения для маятника будет иметь вид: где Решая совместно уравнения (6) и (8), определим
Выражая Т из (6) и подставляя в (8), получим:
Как следует из (6) движение груза m является равноускоренным (силы, приложенные к грузу постоянны), и поэтому, учтя, что v0 = 0, получим За время t груз проходит расстояние h, равное высоте поднятия груза над подставкой, измерив время падения груза и высоту h, получим a = 2 h/t 2. (11) Подставив последнее равенство в (8), получим
Ускорение груза а равно тангенциальному ускорению вращающегося маятника аt, т.е.
Момент инерции маятника найдем, решая совместно (4), (11) и (12): 3. Экспериментальная часть Описание экспериментальной установки Общая схема экспериментальной установки представлена на рис. 2. На шкиве 2 радиуса R закреплены четыре стержня одинаковой длины, вдоль которых могут свободно перемещаться грузы 3 массой m 0. К шкиву прикрепляется нить 8, перекинутая через неподвижный блок 4, на другой конец которой подвешивается груз 6 общей массой m. На основании с автоматическим таймером 10 установлена подставка 9 с фотоэлектрическим датчиком. К штативу 1 прикреплена линейка 7, показывающая высоту поднятия груза 6. Порядок выполнения работы 1. Определение момента инерции и углового ускорения. 1) наматывая нить на шкив, поднять груз на определенную высоту h. Записать высоту поднятия груза h и радиус шкива R в табл. 1; 2) расположить грузы m 0 на одинаковом расстоянии от оси вращения крестовины (например, на концах осей маятника Обербека); 3) измерить три раза время падения груза с одной массой m. Занести данные в табл. 1; 4) опыт проделать три раза с различными массами груза т. Занести данные в табл. 1. Таблица 1
2. Исследование зависимости e и JZ от расположения масс на крестовине маятника. Проделать предыдущий опыт для различных положений грузов m 0 на осях крестовины (размещая грузы симметрично у основания крестовины, в середине и по краям). Массу груза m не изменять. Результаты занести в табл. 2. Таблица 2
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 328; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.108 (0.005 с.) |

 , (1)
, (1) где
где  – вектор, проведенный из точки О в точку приложения силы
– вектор, проведенный из точки О в точку приложения силы  .
.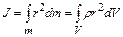 , (2)
, (2) , (3)
, (3) , действуя на тело с моментом инерции J, закрепленное на оси Z, вызывает угловое ускорение e
, действуя на тело с моментом инерции J, закрепленное на оси Z, вызывает угловое ускорение e  , (4)
, (4) где МZ - проекция вектора
где МZ - проекция вектора  , (5)
, (5)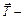 сила натяжения нити.
сила натяжения нити. . (6)
. (6) , причем
, причем  . Эта сила создает вращательный момент, проекция которого на ось вращения Z равна MZ = R T, (7)
. Эта сила создает вращательный момент, проекция которого на ось вращения Z равна MZ = R T, (7)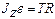 , (8)
, (8)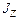 – момент инерции, рассчитываемый по формуле (3),
– момент инерции, рассчитываемый по формуле (3),  .
.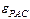 :
: (9)
(9) . (10)
. (10) .
. . (12)
. (12) , следовательно,
, следовательно, . (13)
. (13) . (14)
. (14) рад/с2
рад/с2



