
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Исследование упругого соударения шаровСодержание книги
Поиск на нашем сайте
Цель работы: экспериментальное определение импульсов двух упруго соударяющихся шаров до и после соударения. Проверка выполнения закона сохранения импульса для замкнутой системы тел.
Теоретическое введение В физике взаимодействие тел может быть рассмотрено на простейшей модели – центрального удара двух шаров. Удар называется центральным, если шары до удара движутся вдоль прямой, проходящей через их центры. Существуют два предельных вида удара: абсолютно упругий и неупругий удары. Эти взаимодействия шаров принципиально отличаются друг от друга. При абсолютно неупругом ударе кинетическая энергия движущихся шаров полностью или частично превращается в их внутреннюю энергию (тепло, энергию остаточных деформаций). После удара шары движутся с одинаковой скоростью, как единое целое, либо покоятся. При абсолютно неупругом ударе выполняется только закон сохранения импульса, закон же сохранения механической энергии не соблюдается. В случае абсолютно упругого удара кинетическая энергия обоих шаров сначала превращается в потенциальную энергию упругих деформаций тел. Затем тела возвращаются к первоначальной форме, отталкивая друг друга. В итоге потенциальная энергия упругих деформаций снова переходит в кинетическую энергию движущихся шаров. При центральном абсолютно упругом ударе выполняются закон сохранения механической энергии и закон сохранения импульса замкнутой системы тел (шаров). На основе этих законов сохранения можно получить выражение для расчета скоростей шаров после абсолютно упругого удара. Закон сохранения импульса имеет вид
а закон сохранения энергии
где Рассмотрим случай, когда один из шаров массой
Совместное решение системы уравнений (5.3) и (5.4) (с учетом того, что центры шаров движутся по одной прямой) позволяет определить скорости шаров после удара:
Методика измерений
Получим рабочие формулы для вычисления скоростей шаров
где
Следовательно,
Подставляя (5.9) в (5.7), получим:
Значение скоростей шаров в точке
Суммарный импульс системы шаров до первого удара
После первого удара левый шар получает импульс
а правый шар останавливается (см. (5.5), Суммарный импульс системы шаров после 1-го удара
После 2-го удара правый шар получает импульс
а левый шар останавливается ( Тогда суммарный импульс системы шаров после 2-го удара
Для проверки выполнения закона сохранения импульса необходимо сравнить суммарный импульс системы шаров до и после 1-го и 2-го ударов. После проведения прямых измерений углов
Экспериментальная часть
Приборы и оборудование: экспериментальная установка для изучения центрального удара шаров.
Изучаемый объект представляет собой два одинаковых шара, подвешенных на нитках равной длины. Центры масс шаров лежат в горизонтальной плоскости на расстоянии, равном расстоянию между точками подвеса нитей. Диаметры шаров составляют
Правый шар 5 отклоняют вправо на некоторый угол
|
||||
|
Последнее изменение этой страницы: 2016-06-06; просмотров: 203; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.225.92.116 (0.009 с.) |

 , (5.1)
, (5.1)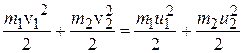 (5.2)
(5.2) ,
,  – массы шаров;
– массы шаров;  и
и  – скорости шаров до удара;
– скорости шаров до удара; 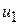 и
и  – скорости шаров после удара.
– скорости шаров после удара. . Тогда законы сохранения импульса и механической энергии запишутся в форме:
. Тогда законы сохранения импульса и механической энергии запишутся в форме: , (5.3)
, (5.3) . (5.4)
. (5.4)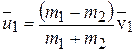 , (5.5)
, (5.5)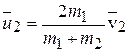 . (5.6)
. (5.6) В лабораторной работе исследуется центральный упругий удар шаров, когда до удара шары сближаются по линии, проходящей через их центры масс (рис.5.1). Такой удар реализуется в установке с двумя подвешенными на нитях равной длины шарами. Расстояние между точками подвеса равно сумме радиусов обоих шаров.
В лабораторной работе исследуется центральный упругий удар шаров, когда до удара шары сближаются по линии, проходящей через их центры масс (рис.5.1). Такой удар реализуется в установке с двумя подвешенными на нитях равной длины шарами. Расстояние между точками подвеса равно сумме радиусов обоих шаров. Пусть левый шар массой
Пусть левый шар массой 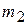 до удара покоится. Выведем из положения равновесия правый шар массой
до удара покоится. Выведем из положения равновесия правый шар массой  и отпустим. Скорости шаров после удара можно определить по углам отклонения
и отпустим. Скорости шаров после удара можно определить по углам отклонения  и
и  первого и второго шаров от положения равновесия.
первого и второго шаров от положения равновесия.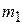 , отклоненного на угол
, отклоненного на угол  , полностью преобразуется в его кинетическую энергию, запишем
, полностью преобразуется в его кинетическую энергию, запишем (5.7)
(5.7) – высота подъема шара (рис. 5.2);
– высота подъема шара (рис. 5.2);  – ускорение свободного падения. Как видно из прямоугольного треугольника ABC на рис.5.2,
– ускорение свободного падения. Как видно из прямоугольного треугольника ABC на рис.5.2, . (5.8)
. (5.8) (5.9)
(5.9) , или
, или (5.10)
(5.10)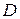 непосредственно после удара определяется аналогично по углам отклонения от положения равновесия 1-го (правого)
непосредственно после удара определяется аналогично по углам отклонения от положения равновесия 1-го (правого)  и 2-го (левого) шаров
и 2-го (левого) шаров  :
: (5.11)
(5.11) , (5.12)
, (5.12) (5.13)
(5.13) , (5.14)
, (5.14) ;
;  ).
). (5.15)
(5.15)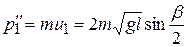 , (5.16)
, (5.16) ).
). (5.17)
(5.17) мм. Массы шаров
мм. Массы шаров  . Шары изготовлены из специального полимерного материала. Анализ физико-химических свойств этого полимера позволяет считать, что при соударении шаров условия (5.1) и (5.2) реализуются с хорошей точностью.
. Шары изготовлены из специального полимерного материала. Анализ физико-химических свойств этого полимера позволяет считать, что при соударении шаров условия (5.1) и (5.2) реализуются с хорошей точностью. Внешний вид установки представлен на рис 5.3. Основание 1 установлено строго горизонтально на лабораторном столе через регулируемые антивибрирующие ножки 2. На верхнем конце штанги 3, закрепленной перпендикулярно основанию, предусмотрен механизм подвеса 4. Он позволяет регулировать длину нитей подвеса шаров 5 и 6 и расстояние между точками подвеса. Для регистрации угловых положений шаров 5 и 6 на основании установлены две шкалы: шкала А – для правого шара 5 и шкала В – для левого шара 6. Таким образом, углы
Внешний вид установки представлен на рис 5.3. Основание 1 установлено строго горизонтально на лабораторном столе через регулируемые антивибрирующие ножки 2. На верхнем конце штанги 3, закрепленной перпендикулярно основанию, предусмотрен механизм подвеса 4. Он позволяет регулировать длину нитей подвеса шаров 5 и 6 и расстояние между точками подвеса. Для регистрации угловых положений шаров 5 и 6 на основании установлены две шкалы: шкала А – для правого шара 5 и шкала В – для левого шара 6. Таким образом, углы 


