
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Лабораторная установка и методика измеренийСодержание книги
Поиск на нашем сайте
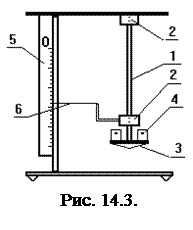
Установка для измерения схематически показана на рис. 14.3. Исследуемый образец (резиновый шнур) 1 имеет на концах металлические зажимы 2. Верхний зажим закреплен неподвижно к штативу, к нижнему зажиму подвешена платформа 3 для размещения гирь 4. Параллельно образцу закреплена линейка 5. На шкале линейки 5 находится стрелка 6, основание которой закреплено на нижнем зажиме. При растяжении образца стрелка перемещается на величину абсолютного удлинения.
Порядок выполнения работы
1. При свободной от гирь платформе штангенциркулем измерьте диаметр ненагруженного образца Таблица 14.1
2. По шкале линейки найдите длину ненагруженного образца 3. Найдите начальное положение стрелки 4. Ставьте на платформу грузы парами (симметрично подвесу во избежание перекоса). Каждый раз отмечайте показания стрелки 5. При максимальной нагрузке штангенциркулем измерьте диаметр образца 6. Для проверки применимости закона Гука постройте графики зависимости модуля Юнга 7. Рассчитайте ошибку определения модуля Юнга 8. Значения модуля Юнга, совпадающие с учетом ошибки 9. Определите значение коэффициента Пуассона. 10. Сделайте выводы. Замечание: относительная погрешность модуля Юнга может быть рассчитана по формуле:
Контрольные вопросы
1. Что такое модуль Юнга? От чего он зависит? 2. Как связаны жёсткость и модуль Юнга? 3. Что такое абсолютное и относительное удлинение образца? 4. Что такое механическое напряжение? 5. Что такое коэффициент Пуассона? 6. Что такое абсолютное и относительное поперечное сжатие? 7. Какие из перечисленных характеристик относятся к материалу? 8. Какие из перечисленных характеристик относятся к образцу? 9. Сформулируйте закон Гука. 10. Нарисуйте кривую зависимости 11. Что такое деформация сдвига? 12. Что такое пластическая деформация? Поясните рисунком на примере деформации сдвига. 13. В чем состоит суть данного метода измерения модуля Юнга 14. Какие размерности у 15. Каков порядок величин 16. Учитывается ли в опыте масса самого образца? 17. Почему в лабораторной работе используется резиновый образец, а, например, не стальной?
Используемая литература
[1] §14; [7] §21; [4] §48; [10] §29.
Лабораторная работа 1-15 Определение модуля Юнга методом прогиба
Цель работы: определение модуля Юнга материала путем измерения прогиба образца при нагрузке.
Теоретическое введение
Внимание! Перед выполнением работы 1-15 рекомендуется прочитать теоретическое введение к лабораторной работе 1-14.
Прочность, долговечность и надежность металлических изделий (твердых тел), работающих в различных условиях, во многом зависит от характеристик, определяющих упругие свойства материалов. Твердые тела при этом будем рассматривать как сплошную среду с определенной плотностью
В отличие от растяжения и сжатия деформация сдвига вызывается касательными напряжениями
где
где
Из (15.3) следует, что в твердых телах
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-06-06; просмотров: 197; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.6.9 (0.008 с.) |

 В нашем опыте роль внешней силы
В нашем опыте роль внешней силы  играет сила тяжести
играет сила тяжести  . Из определения напряжения
. Из определения напряжения  , закона Гука
, закона Гука  для цилиндрического образца диаметром
для цилиндрического образца диаметром  , искомое соотношение для модуля Юнга имеет вид:
, искомое соотношение для модуля Юнга имеет вид: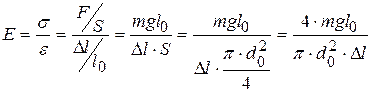 . (14.7)
. (14.7) ,
, 
 , мм
, мм

 , мм
, мм
 , мм
, мм

 , мм
, мм
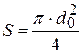 ,
, 

 ,
, 



 . За концы образца можно принимать внутренние концы зажимов. Оцените погрешность этой величины
. За концы образца можно принимать внутренние концы зажимов. Оцените погрешность этой величины  .
. . Положение стрелки отмечают с точностью 0.5 мм, то есть погрешность измерения удлинения равна
. Положение стрелки отмечают с точностью 0.5 мм, то есть погрешность измерения удлинения равна  .
. от напряжений
от напряжений  .
.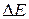 (достаточно рассчитать для одного опыта).
(достаточно рассчитать для одного опыта). , позволяют определить истинное (среднее) значение модуля Юнга. С учетом этого определите среднее значение модуля Юнга.
, позволяют определить истинное (среднее) значение модуля Юнга. С учетом этого определите среднее значение модуля Юнга. .
. и расскажите о ее характерных точках и участках.
и расскажите о ее характерных точках и участках. ?
? . Под воздействием внешних сил твердые тела в той или иной степени деформируются, то есть изменяют свою форму и объем. При всем разнообразии деформаций тел любую деформацию можно свести к двум основным (элементарным): растяжению (сжатию) и сдвигу.
. Под воздействием внешних сил твердые тела в той или иной степени деформируются, то есть изменяют свою форму и объем. При всем разнообразии деформаций тел любую деформацию можно свести к двум основным (элементарным): растяжению (сжатию) и сдвигу. Сдвигом называется такая деформация твердого тела, при которой все его плоские слои, параллельные некоторой неподвижной плоскости, называемой плоскостью сдвига, не искривляясь и не изменяясь в размерах, смещаются параллельно друг другу (рис.15.1). Деформация сдвига характеризуется величиной относительного сдвига. При малых деформациях сдвига относительный сдвиг есть просто измеренный в радианах угол
Сдвигом называется такая деформация твердого тела, при которой все его плоские слои, параллельные некоторой неподвижной плоскости, называемой плоскостью сдвига, не искривляясь и не изменяясь в размерах, смещаются параллельно друг другу (рис.15.1). Деформация сдвига характеризуется величиной относительного сдвига. При малых деформациях сдвига относительный сдвиг есть просто измеренный в радианах угол 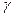 . При деформации однородного сдвига величина
. При деформации однородного сдвига величина  во всех точках тела одна и та же.
во всех точках тела одна и та же.
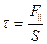 , (15.1)
, (15.1) – сила, параллельная поверхности твердого тела площадью
– сила, параллельная поверхности твердого тела площадью  и вызывающая сдвиг. При малых деформациях закон Гука в этом случае имеет вид, аналогичный (14.3):
и вызывающая сдвиг. При малых деформациях закон Гука в этом случае имеет вид, аналогичный (14.3): , (15.2)
, (15.2) – коэффициент пропорциональности между напряжением сдвига
– коэффициент пропорциональности между напряжением сдвига  . (15.3)
. (15.3) .
.


