
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Определение динамического коэффициента вязкостиСодержание книги
Поиск на нашем сайте
Цель работы: определение коэффициента вязкости воздуха.
Теоретическое введение
В практикуме три лабораторных работы посвящены определению коэффициента вязкости. В работе 1-18 изучается стационарное течение жидкости; в работе 1-17 и данной работе – в газе. Во всех трех работах используется формула Пуазейля для объема вещества, который протекает за единицу времени через поперечное сечение трубы. Жидкость и газ обладают общими чертами, отличающими их от твердых тел. Так, всякий объем жидкости или газа способен как угодно изменять свою форму под действием сколь угодно малых сил. Это их общее свойство. Общая черта жидкостей и газов состоит также в том, что только в отношении деформации всестороннего сжатия (изменения объема) они ведут себя как упругие тела. Напомним, что из двух элементарных деформаций – сжатия (растяжения) и сдвига только первая связана с изменением объема. Элементарная деформация сдвига, как было сказано, не сопровождается изменением объема. Все же при быстрых деформациях сдвига в жидкостях и газах могут возникать заметные силы; однако эти силы зависят не от величины деформации, а от скорости изменения деформации. И если скорость деформации стремится к нулю, то и силы стремятся к нулю. Поэтому эти силы следует рассматривать не как упругие силы, а как силы трения – это силы внутреннего трения, или силы вязкости. Поскольку в этой работе реализована только несколько другая методика измерения коэффициента вязкости, то теоретическое введение следует изучать по работе 1-17, там же представлен и вывод формулы Пуазейля.
Экспериментальная часть
Приборы и оборудование: стеклянный сосуд с краном, пробка с капилляром, штатив, секундомер, мерный стакан (колба), линейка, вода.
В предлагаемом методе определения динамического коэффициента вязкости используется истечение воздуха через капилляр. Известно, что скорости истечения бесконечно тонких цилиндрических слоев воздуха, расположенных на различных расстояниях от оси капилляра, различны и распределены по сечению капилляра по параболическому закону. Наибольшая скорость будет на осевой линии капилляра и, по мере приближения к стенкам, скорость уменьшается, а слой, прилегающий к стенке, неподвижен, т.е. "прилипает" к ней. Между слоями, движущимися с различными скоростями, возникает сила внутреннего трения (сила вязкости). При установившемся движении сила вязкости, действующая на элементарный объем и приложенная к боковой поверхности цилиндра, уравновешивает разность сил давлений, действующих на основание цилиндра. На концах капилляра при протекании по нему воздуха возникает разность давлений
отсюда
где Таким образом, для определения коэффициента вязкости достаточно измерить разность давлений, время истечения газа, его объем, радиус и длину капилляра.
Это давление уравновешивается атмосферным:
Учитывая, что давление у верхнего конца капилляра равно атмосферному, разность давлений на концах капилляра выразится:
Поскольку в процессе опыта давление столба воды уменьшается (за счет истечения), то берут среднее значение
и выражение для коэффициента динамической вязкости примет вид:
Порядок выполнения работы 1. Подготовьте установку к выполнению работы: a) залейте сосуд на 3/4 объема водой; b) закройте сверху плотно трубкой с капилляром; c) подставьте под кран сливную емкость; d) подготовьте к работе секундомер. 2. Откройте кран К. Когда вода начнет вытекать каплями: a) отметьте уровень воды h 1; b) подставьте мерный сосуд под трубку D; c) запустите секундомер. 3. Когда в мерном сосуде будет 50 мл воды: a) отметьте по шкале новый уровень воды h 2. При этом объем воды в мерном сосуде равен объему прошедшего через капилляр воздуха; b) одновременно с этим остановите секундомер. Результаты измерений занесите в таблицу 19.1. 4. Опыт повторите ещё 4 раза. При этом для очередного опыта значение h 1 будет равно значению h 2 для предыдущего. 5. В каждом опыте рассчитайте по формуле (19.2) коэффициент вязкости 6. Выведите формулу для вычисления погрешности D h. 7. Результаты вычислений занесите в таблицу 19.1. Таблица 19.1
Контрольные вопросы 1. Какими общими чертами обладают жидкости и газы? 2. Почему возможно в лабораторных работах 1-17, 1-18 использовать формулу Пуазейля для определения коэффициента вязкости, хотя в работе 1-18 измеряют свойства жидкостей, а в 1-17 – газа? 3. Каков физический смысл коэффициента динамической вязкости? 4. Запишите формулу Ньютона для силы вязкости. 5. От каких параметров и как зависит коэффициент вязкости воздуха? 6. Запишите формулу Пуазейля. 7. Выведите рабочую формулу для коэффициента вязкости.
Используемая литература [2] §128-130; [3] §10.6-10.8; [7] §48; [4] §2.27-2.29; [10] §16.2; [11] §25. Лабораторная работа 1-20
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-06-06; просмотров: 286; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.135.214.226 (0.009 с.) |

 . При установившемся движении воздуха она будет неизменной. При малых скоростях течения объем воздуха, протекающего через сечение капилляра, равен:
. При установившемся движении воздуха она будет неизменной. При малых скоростях течения объем воздуха, протекающего через сечение капилляра, равен:
 . (19.1)
. (19.1) – радиус капилляра;
– радиус капилляра; 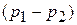 – разность давлений в начале и конце капилляра;
– разность давлений в начале и конце капилляра; 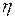 – динамический коэффициент вязкости;
– динамический коэффициент вязкости;  – длина капилляра;
– длина капилляра;  – объем газа, протекшего через сечение капилляра за время
– объем газа, протекшего через сечение капилляра за время 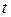 .
. Схема установки представлена на рис. 19.1. Установка состоит из стеклянного сосуда А со шкалой C. Верхняя часть сосуда закрыта пробкой с капилляром B, а в нижней имеется трубка с краном К. Перед началом работы кран закрыт, сосуд заполнен водой на 3/4 объема и плотно закрыт пробкой с капилляром. Если открыть кран К, то вода из сосуда А будет вытекать каплями. При этом объем воды, вытекающий из сосуда, равен объему воздуха, прошедшего через капилляр, а давление у открытого конца трубки D равно сумме давлений: давления
Схема установки представлена на рис. 19.1. Установка состоит из стеклянного сосуда А со шкалой C. Верхняя часть сосуда закрыта пробкой с капилляром B, а в нижней имеется трубка с краном К. Перед началом работы кран закрыт, сосуд заполнен водой на 3/4 объема и плотно закрыт пробкой с капилляром. Если открыть кран К, то вода из сосуда А будет вытекать каплями. При этом объем воды, вытекающий из сосуда, равен объему воздуха, прошедшего через капилляр, а давление у открытого конца трубки D равно сумме давлений: давления  воздуха, находящегося над поверхностью воды в сосуде А, и гидростатического давления
воздуха, находящегося над поверхностью воды в сосуде А, и гидростатического давления  :
: .
. .
.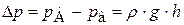 .
. ,
,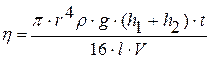 . (19.2)
. (19.2)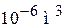
 ,
с
,
с

 , %
, %



