
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Относительность понятия одновременности.Содержание книги
Поиск на нашем сайте
Рассмотрим инерциальные системы отсчета KА и KВ.
а — Система KВ движется относительно системы KА вправо; следовательно, KА играет роль системы K, а KВ — роль системы K', б — Система Kв движется относительно системы KА влево; это равнозначно тому, что KА движется относительно KВ вправо; следовательно, KА играет роль системы K', а KВ — роль системы K.
Предположим, что в системе KА в точках с координатами x1А и x2А (x2А > x1А) происходят в момент времени tA два одновременных события. Найдем разность моментов времени t2B и t1B, в которые будут зарегистрированы эти события в системе KB. Если система KB движется относительно KА вправо (рис. a), то, применяя преобразования Лоренца, KA нужно считать системой K, а KB —системой K' и пользоваться для вычисления моментов времени t1B и t2B формулами (111). В этом случае
Соответственно
Если же система KB движется относительно КA влево (рис.б), то KА нужно считать системой K', а KB —системой K и пользоваться другой формулой. В этом случае
Таким образом, в любой системе, кроме KA, события оказываются неодновременными, причем в одних системах второе событие будет происходить позже первого (t2B > t1B), а в других системах второе событие будет происходить раньше первого (t2B < t1B). Нужно иметь в виду, что полученный нами результат относится лишь к событиям, причинно не связанным друг с другом (очевидно, что события, происходящие одновременно в разных точках пространства, не могут оказывать воздействия друг на друга). Иначе обстоит дело, если между событиями имеется причинная связь. В этом случае событие-причина во всех системах отсчета предшествует событию ‑ следствию. Рождение элементарной частицы во всех системах отсчета происходит раньше ее распада. Ни в одной из систем «сын не рождается раньше отца». Длина тел в разных системах отсчета. Сравним длину стержня в инерциальных системах отсчета K и K ' (рис.). Предположим, что стержень, расположенный вдоль совпадающих осей x и x' покоится всистеме K'. Тогда определение его длины в этой системе не доставляет хлопот. Нужно приложить к стержню масштабную линейку и определить координату x'1 одного конца стержня, а затем координату x'2 другого конца. Разность координат даст длину стержня l0 в системе K': l0 = x'2 ‑ x'1.
Стержень покоится в системе K'. Относительно системы K он движется со скоростью v, равной относительной скорости систем V. В системе K дело обстоит сложнее. Относительно этой системы стержень движется со скоростью v, равной скорости V, с которой система K' движется относительно системы K. (Обозначение V мы будем употреблять только применительно к относительной скорости систем отсчета.) Поскольку стержень движется, нужно произвести одновременный отсчет координат его концов x1 и x2 в некоторый момент времени t. Разность координат даст длину стержня l в системе K: l = x2 ‑ x1. Для сопоставления длин l и l0 нужно взять ту из формул преобразований Лоренца, которая связывает координаты x, x' и время t системы K, т. е. первую из формул (113). Подстановка в нее значений координат и времени приводит к выражениям
Отсюда
(мы подставили вместо β его значение). Заменив разности координат длинами стержня, а относительную скорость V систем K и K' равной ей скоростью стержня v, с которой он движется в системе K, придем к формуле
Таким образом, длина движущегося стержня оказывается меньше той, которой обладает стержень в состоянии покоя. Аналогичный эффект наблюдается для тел любой формы: в направлении движения линейные размеры тела сокращаются тем больше, чем больше скорость движения. Это явление называется лоренцевым (или фицджеральдовым) сокращением. Поперечные размеры тела не изменяются. В результате, например, шар принимает форму эллипсоида, сплющенного в направлении движения. Можно показать, что зрительно этот эллипсоид будет восприниматься в виде шара. Это объясняется искажением зрительного восприятия движущихся предметов, вызванным неодинаковостью времен, которые затрачивает свет на прохождение пути от различно удаленных точек предмета до глаза. Искажение зрительного восприятия приводит к тому, что движущийся шар воспринимается глазом как эллипсоид, вытянутый в направлении движения. Оказывается, что изменение формы, обусловленное лоренцевым сокращением, в точности компенсируется искажением зрительного восприятия. Промежуток времени между событиями. Пусть в системе K' в одной и той же точке с координатой x' происходят в моменты времени t'1 и t'2 два каких-то события. Это могут быть, например, рождение элементарной частицы и ее последующий распад. В системе K' эти события разделены промежутком времени D t ' = t '2 ‑ t '1. Найдем промежуток времени D t между событиями в системе K, относительно которой система K' движется со скоростью V. Для этого определим в системе K моменты времени t1 и t2, соответствующие моментам t'1 и t'2 и образуем их разность: D t = t 2 — t 1. Подстановка в нее значений координаты и моментов времени приводит к выражениям
Отсюда Если события происходят с одной и той же частицей, покоящейся в системе K', то D t' = t'2 — t'1 представляет собой промежуток времени, измеренный по часам, неподвижным относительно частицы и движущимся вместе с ней относительно системы K со скоростью v, равной V (напомним, что буквой V мы обозначаем только относительную скорость систем; скорости частиц и часов мы будем обозначать буквой v). Время, отсчитанное по часам, движущимся вместе с телом, называется собственным временем этого тела и обычно обозначается буквой τ. Следовательно, D t' = Dτ. Величина D t == t2 — t1 представляет собой промежуток времени между теми же событиями, измеренный по часам системы K, относительно которой частица (вместе со своими часами) движется со скоростью v. С учетом сказанного Из полученной формулы следует, что собственное время меньше времени, отсчитанного по часам, движущимся относительно тела (очевидно, что часы, неподвижные в системе K, движутся относительно частицы со скоростью — v). В какой бы системе отсчета не рассматривалось движение частицы, промежуток собственного времени измеряется по часам системы, в которой частица покоится. Отсюда следует, что промежуток собственного времени является инвариантом, т. е. величиной, имеющей одно и то же значение во всех инерциальных системах отсчета. С точки зрения наблюдателя, «живущего» в системе K, D t есть промежуток времени между событиями, измеренный по неподвижным часам, а Dτ— промежуток времени, измеренный по часам, движущимся со скоростью v. Поскольку Dτ < D t, можно сказать, что движущиеся часы идут медленнее, чем покоящиеся часы. Подтверждением этого служит следующее явление. В составе космического излучения имеются рождающиеся на высоте 20—30 км нестабильные частицы, называемые мюонами. Они распадаются на электрон (или позитрон) и два нейтрино. Собственное время жизни мюонов (т. е. время жизни, измеренное в системе, в которой они неподвижны) составляет в среднем примерно 2 мкс. Казалось бы, что даже двигаясь со скоростью, очень мало отличающейся от c, они могут пройти лишь путь, равный 3·108·2·10‑6 м. Однако, как показывают измерения, они успевают в значительном количестве достигнуть земной поверхности. Это объясняется тем, что мюоны движутся со скоростью, близкой к c. Поэтому их время жизни, отсчитанное по часам, неподвижным относительно Земли, оказывается значительно большим, чем собственное время жизни этих частиц. Следовательно, не удивительно, что экспериментатор наблюдает пробег мюонов, значительно превышающий 600 м. Для наблюдателя, движущегося вместе с мюонами, расстояние до поверхности Земли сокращается до 600 м, поэтому мюоны успевают пролететь это расстояние за 2 мкс. Интервал В обычном пространстве расстояние Dl между двумя точками с координатами xi, у1, z1 и x2, у2, z2. определяется выражением
где D x = x2 ‑ x1 и т. д. Это расстояние не зависит от выбора системы координат, т. е. является инвариантом. При переходе к другой координатной системе изменяются, вообще говоря, величины D x, D y и D z, однако эти изменения таковы, что расстояние Dl остается одним и тем же. Казалось бы, что расстояние (или, как принято говорить, интервал) между двумя мировыми точками в четырехмерном пространстве-времени должно определяться аналогичным выражением
где D t = t2 ‑ t1 и т. д. Однако это выражение непригодно в качестве интервала, поскольку оно не является инвариантом — при переходе к другой инерциальной системе отсчета числовое значение этого выражения изменяется. Инвариантным, как мы покажем, является выражение
которое называют интервалом между событиями. Величина D s является аналогом расстояния Dl между точками в обычном пространстве. Причина того, что интервал определяется не выражением а выражением заключается в том, что, как говорят, метрика пространства-времени отличается от метрики обычного трехмерного пространства. В обычном пространстве справедлива евклидова геометрия, вследствие чего его называют евклидовым. Качественное различие между временем и пространством приводит к тому, что в выражение для интервала квадрат временной координаты и квадраты пространственных координат входят с разными знаками. Пространство, в котором расстояние между точками определяется выражением вида
где Dl — расстояние между точками обычного пространства, в которых произошли данные события. Допустим, что рассматриваются события, происходящие с одной и той же частицей. Тогда отношение Dl/D t дает скорость частицы v. Поэтому, вынеся из-под корня c D t, получим, что
Мы получили выражение D s = c ·Dτ. Поскольку c — константа, а Dτ —инвариант, интервал D s также оказывается инвариантом. 1.11.4. Преобразование и сложение скоростей. Компоненты скорости частицы v в системе K определяются выражениями
В системе K' компоненты скорости v той же частицы равны
Найдем формулы, связывающие нештрихованные компоненты скорости со штрихованными.
Окончательно получим
Аналогично Релятивистский импульс. Выражение, обеспечивающее инвариантность закона сохранения импульса, может быть получено, если вместо времени t подставить собственное время τ. Тогда
|
|||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 525; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.147.82.108 (0.009 с.) |


 ,
, 
 .
. ;
;  .
. .
.

 .
. .
. .
.
 .
. .
. .
. ,
, ,
, ,
, ,
,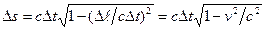 .
. . Оно равно Dτ — промежутку собственного времени частицы между событиями. Таким образом, мы приходим к соотношению
. Оно равно Dτ — промежутку собственного времени частицы между событиями. Таким образом, мы приходим к соотношению




 .
.


