
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Достаточное условие возрастания и убывания функцииСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Пусть f(x) – дифференцируемая функция на некотором промежутке. Если в каждой точке х данного промежутка ¦¢(х)>0, то функция f(x) возрастает на этом промежутке, если же в каждой точке х этого промежутка ¦¢(х)<0, то функция f(x) убывает. Интервалы, на которых функция возрастает (убывает), называются интервалами монотонности функции. Если производная f '(x) непрерывна, то разделять интервалы монотонности функции могут лишь точки, в которых f '(x) = 0. Такие точки называются стационарными точками функции f(x). Если не требовать непрерывности производной f '(x), то интервалы монотонности могут разделять точки, в которых f '(x) не существует. Точки, в которых f '(x) = 0 либо f '(x) не существует называются критическими точками функции f(x). Замечание. Не каждая критическая точка разделяет интервалы монотонности. Например, функции у = х2 и у = х3 имеют критическую точку х = 0. Эта точка для функции у = х2 разделяет, а для функции у = х3 не разделяет интервалы монотонности. · Правило Лопиталя Правило Бернулли[1]-Лопита́ля — метод нахождения пределов функций, раскрывающий неопределённости вида . Пусть для функций f(x), g(x) в окрестностях точки а выполняются условия Коши, причем, f(a) = g(a) = 0 и существует предел lim f‘(x)/g’(x), x тогда lim f(x) = {0/0} = lim f‘(x) (24) x Док – во. По теореме Коши существует такая точка c g’(c) g(x) - 0 В этом равенстве перейдем к пределу x lim f(x) = lim f’(c) = lim f’(c) = lim f’(x) x т.к. процесс x · Общая схема исследования функции и построения графика Найти точки пересечения графика функции с осями координат. 1. Провести исследование функции с помощью первой производной, то есть найти точки экстремума функции и интервалы возрастания и убывания. 2. Исследовать функцию с помощью производной второго порядка, то есть найти точки перегиба графика функции и интервалы его выпуклости и вогнутости. 3. Найти асимптоты графика функции: а) вертикальные, b) наклонные. 4. На основании проведенного исследования построить график функции. Заметим, что перед построением графика полезно установить, не является ли данная функция четной или нечетной. Вспомним, что функция называется четной, если при изменении знака аргумента значение функции не меняется: f(-x) = f(x) и функция называется нечетной, если f(-x) = -f(x). В этом случае достаточно исследовать функцию и построить её график при положительных значениях аргумента, принадлежащих ОДЗ. При отрицательных значениях аргумента график достраивается на том основании, что для четной функции он симметричен относительно оси Oy, а для нечетной относительно начала координат. · Функции нескольких переменных. Понятие предела функции 2-х переменных. Непрерывность функции 2-х переменных
· Определение. Если каждой паре (x, y) значений двух независимых переменных из области Wставится определенное значение z, то говорят, что z есть функция двух переменных (x, y).
Полное приращение функции
Частное приращение функции Вообще, полное приращение функции не равно сумме частных приращений. 1. Непрерывность функции нескольких переменных Предел функции. Пусть z = f (x, y) определена в некоторой окрестности A (x 0, y 0). Определение. Постоянное число b называют пределом z = f (x, y) при P (x, y) стремящемся к A, если для любого e > 0 можно указать такое значение d > 0, что для всех x, удовлетворяющих неравенству | AP | < d, имеет место неравенство | f (x, y)- b | < e. 2. Непрерывная функция 3. Частные производные Рассмотрим плоскость и систему Oxy декартовых прямоугольных координат на ней (можно рассматривать и другие системы координат). Из аналитической геометрии знаем, что каждой упорядоченной паре чисел (x, y) можно сопоставить единственную точку M плоскости и наоборот, каждой точке M плоскости соответствует единственная пара чисел. Поэтому в дальнейшем, говоря о точке, мы будем часто подразумевать соответствующую ей пару чисел (x, y) и наоборот. Определение 1.2 Множество пар чисел (x, y), удовлетворяющих неравенствам, называется прямоугольником (открытым). На плоскости он изобразится прямоугольником (рис. 1.2) со сторонами, параллельными осям координат, и с центром в точке M0(x0y0). Прямоугольник принято обозначать следующим символом: Введем важное для дальнейшего изложения понятие: окрестность точки. Определение 1.3 Прямоугольной δ -окрестностью (дельта-окрестностью) точки
с центром в точке M0 и с одинаковыми по длине сторонами 2δ. Определение 1.4 Круговой δ - окрестностью точки M0(x0y0) называется круг радиуса δ с центром в точке M0, т. е. множество точек M(xy), координаты которых удовлетворяют неравенству: Можно ввести понятия окрестностей и других видов, но для целей математического анализа технических задач, в основном, используются лишь прямоугольные и круговые окрестности. Введём следующее понятие предела функции двух переменных. Пусть функция z = f (x, y) определена в некоторой области ζ и M0(x0y0) - точка, лежащая внутри или на границе этой области. Определение 1.5 Конечное число A называется пределом функции f (x, y) при
если для любого положительного числа ε можно найти такое положительное число δ, что неравенство
выполняется для всех точек М(х,у) из области ζ, отличных от M0(x0y0), координаты которых удовлетворяют неравенствам:
Смысл этого определения состоит в том, что значения функции f (х, у) как угодно мало отличаются от числа А в точках достаточно малой окрестности точки М0. Здесь в основу определения положены прямоугольные окрестности М0. Можно было бы рассматривать круговые окрестности точки М0 и тогда нужно было бы требовать выполнения неравенства
во всех точках М(х,у) области ζ, отличных от М0 и удовлетворяющих условию:
- расстояние между точками М и М0. Употребительны следующие обозначения предела: Учитывая определение предела функции двух переменных, можно перенести основные теоремы о пределах для функций одной переменной на функции двух переменных. Например, теоремы о пределе суммы, произведения и частного двух функций. Пусть функция z = f (x,y) определена в точке M0(x0y0) и её окрестности. Определение 1.6 Функция называется непрерывной в точке M0(x0y0), если
25. Частные производные
Частной производной функции нескольких переменных по одной из этих переменных называется предел отношения соответствующего частного приращения функции к приращению рассматриваемо независимой переменной при стремлении последнего к нулю 26. Необходимое и достаточное условия существования функции 2-х переменных Рассмотрим условия существования экстремума функции. Зафиксируем одну из переменных. Положим, например, у=у0. Тогда получим функцию ƒ(х;у0)=φ(х) одной переменной, которая имеет экстремум при х = х0. Следовательно, согласно необходимому условию экстремума функции одной переменной (см. п. 25.4), φ'(х0) = 0, т. е. ƒ'x(х0;y0)=0. Аналогично можно показать, что ƒ'y(х0;у0) = 0. Геометрически равенства ƒ'x(х0;у0)=0 и ƒ'y(х0;у0)=0 означают, что в точке экстремума функции z=ƒ(х;у) касательная плоскость к поверхности, изображающей функцию ƒ(х;у), параллельна плоскости Оху, т. к. уравнение касательной плоскости есть z=z0 (см. формулу (45.2)). Замечание. Функция может иметь экстремум в точках, где хотя бы одна из частных производных не существует. Например, функция имеет максимум в точке О(0;0) (см. рис. 211), но не имеет в этой точке частных производных. Точка, в которой частные производные первого порядка функции z ≈ ƒ(х; у) равны нулю, т. е. f'x=0, f'y=0, называется стационарной точкой функ ции z. Стационарные точки и точки, в которых хотя бы одна частная производная не существует, называются критическими точками. В критических точках функция может иметь экстремум, а может и не иметь. Равенство нулю частных производных является необходимым, но не достаточным условием существования экстремума. Рассмотрим, например, функцию z = ху. Для нее точка О(0; 0) является критической (в ней z'x=у и z'y — х обращаются в ноль). Однако экстремума в ней функция z=ху не имеет, т. к. в достаточно малой окрестности точки О(0; 0) найдутся точки для которых z>0 (точки I и III четвертей) и z < 0 (точки II и IV четвертей). Таким образом, для нахождения экстремумов функции в данной области необходимо каждую критическую точку функции подвергнуть дополнительному исследованию. Тогда: 1. если Δ > 0, то функция ƒ(х;у) в точке (х0;у0) имеет экстремум: максимум, если А < 0; минимум, если А > 0; 2. если Δ < 0, то функция ƒ(х;у) в точке (х0;у0) экстремума не имеет. В случае Δ = 0 экстремум в точке (х0;у0) может быть, может не быть. Необходимы дополнительные исследования. Примем без доказательства.
|
||||||||
|
Последнее изменение этой страницы: 2016-04-21; просмотров: 728; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.96 (0.009 с.) |

 и
и  . Обосновывающая метод теорема утверждает, что при некоторых условиях предел отношения функций равен пределу отношения их производных.
. Обосновывающая метод теорема утверждает, что при некоторых условиях предел отношения функций равен пределу отношения их производных. a
a (a,x), что f‘(c) = f(x) – 0
(a,x), что f‘(c) = f(x) – 0
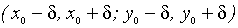

 и
и 


 где
где 

 Если функция f (x,y) непрерывна в точке M0(x0y0), то
Если функция f (x,y) непрерывна в точке M0(x0y0), то



