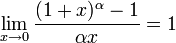Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Абсолютная величина. Понятие окрестности точки.Содержание книги Поиск на нашем сайте Абсолю́тная величина́ или мо́дуль числа Х — неотрицательное число, определение которого зависит от типа числа Х. Обозначается:
Обобщением этого понятия является модуль комплексного числа С геометрической точки зрения, модуль вещественного или комплексного числа есть расстояние между числом и началом координат. В математике широко используется тот факт, что геометрически величина Окре́стность точки — множество, содержащее данную точку, и близкие (в каком-либо смысле) к ней. В разных разделах математики это понятие определяется по-разному. 3. Функция. Способы задания функций. Обратная функция. Функция — математическое понятие, отражающее связь между элементами различных множеств. В самом общем виде, функция — это «закон», по которому каждому элементу одного множества (называемому областью определения) ставится в соответствие некоторый элемент другого множества (называемого областью значений).
Математическое понятие функции выражает интуитивное представление о том, как одна величина полностью определяет значение другой величины. Так значение переменной
Изучением функций занимаются обширные математические теории, такие как математический анализ и функциональный анализ. Обычно рассматриваются числовые функции, которые ставят одни числа в соответствие другим. Такие функции удобно представляются на рисунках в виде графиков.
Способы задания функций
Аналитический способ
Обычно функция задаётся с помощью формулы, в которую входят переменные, операции и элементарные функции. Возможно кусочное задание, то есть различное для различных значений аргумента.
Примеры:
Табличный способ
Функцию можно задать, перечислив все её возможные аргументы и значения для них. После этого, если это необходимо, функцию можно доопределить для аргументов, которых нет в таблице, путём интерполяции или экстраполяции. Примерами могут служить программа передач, расписание поездов или таблица значений булевой функции:
Графический способ
Осциллограмма задаёт значение некоторой функции графически.
Функцию можно задать графически, отобразив множество точек её графика на плоскости. Это может быть приблизительный набросок, как должна выглядеть функция, или показания, снятые с прибора, например, с осциллографа. Этот способ задания может страдать от недостатка точности, однако в некоторых случаях другие способы задания вообще не могут быть применены. Кроме того, такой способ задания один из самых презентативных, удобных для восприятия и качественного эвристического анализа функции.
Рекурсивный способ
Функция может быть задана рекурсивно, то есть через саму себя. В этом случае одни значения функции определяются через другие её значения.
Примеры: факториал; числа Фибоначчи; функция Аккермана.
Словесный способ
Функцию можно описать словами на естественном языке каким-либо однозначным способом, например, описав её входные и выходные значения, или алгоритм, с помощью которого функция задаёт соответствия между этими значениями. Наряду с графическим способом, иногда это единственный способ описать функцию, хотя естественные языки и не столь детерминированы, как формальные.
Примеры: функция, возвращающая цифру в записи числа пи по её номеру; функция, возвращающая число атомов во вселенной в определённый момент времени; функция, принимающая в качестве аргумента человека, и возвращающая число людей, которое родится на свет после его рождения.
Обра́тная фу́нкция — функция, обращающая зависимость, выражаемую данной функцией Функция 4. Основные свойства функций. 1) Область определения функции и область значений функции. Область определения функции - это множество всех допустимых действительных значений аргумента x (переменной x), при которых функция y = f(x) определена. В элементарной математике изучаются функции только на множестве действительных чисел. 2) Нули функции. Нуль функции – такое значение аргумента, при котором значение функции равно нулю. 3) Промежутки знакопостоянства функции. Промежутки знакопостоянства функции – такие множества значений аргумента, на которых значения функции только положительны или только отрицательны. 4) Монотонность функции. Возрастающая функция (в некотором промежутке) - функция, у которой большему значению аргумента из этого промежутка соответствует большее значение функции. Убывающая функция (в некотором промежутке) - функция, у которой большему значению аргумента из этого промежутка соответствует меньшее значение функции. 5) Четность (нечетность) функции. Четная функция - функция, у которой область определения симметрична относительно начала координат и для любого х из области определения выполняется равенство f(-x) = f(x). График четной функции симметричен относительно оси ординат. Нечетная функция - функция, у которой область определения симметрична относительно начала координат и для любого х из области определения справедливо равенство f(-x) = - f(x). График нечетной функции симметричен относительно начала координат. 6) Ограниченная и неограниченная функции. Функция называется ограниченной, если существует такое положительное число M, что |f(x)| ≤ M для всех значений x. Если такого числа не существует, то функция - неограниченная. 7) Периодическость функции. Функция f(x) - периодическая, если существует такое отличное от нуля число T, что для любого x из области определения функции имеет место: f(x+T) = f(x). Такое наименьшее число называется периодом функции. Все тригонометрические функции являются периодическими. (Тригонометрические формулы). Изучив данные свойства функции Вы без проблем сможете исследовать функцию и по свойствам функции сможете построить график функции. Также посмотрите материал про таблицу истинности, таблицу умножения, таблицу Менделеева, таблицу производных и таблицу интегралов.
свойства основных элементарных функций по схеме: · область определения функции; · поведение функции на границах области определения, вертикальные асимптоты (при необходимости смотрите статью классификация точек разрыва функции); · проверка на четность и нечетность; · область значений функции; · промежутки возрастания и убывания, точки экстремума; · промежутки выпуклости (выпуклости вверх) и вогнутости (выпуклости вниз), точки перегиба (при необходимости смотрите статью выпуклость функции, направление выпуклости, точки перегиба, условия выпуклости и перегиба); · наклонные и горизонтальные асимптоты; · особые точки функций; · особые свойства некоторых функций (например, наименьший положительный период у тригонометрических функций).
6. Предел числовой последовательности. Предел числовой последовательности — предел последовательности элементов числового пространства. Числовое пространство — это метрическое пространство, расстояние в котором определяется как модуль разности между элементами. Поэтому,предел числовой последовательности — это такое число, что для всякой сколь угодно малой величины существует номер, начиная с которого уклонение членов последовательности от данной точки становится меньше заранее заданной величины. Понятие предела последовательности вещественных чисел формулируется совсем просто, а в случае комплексных чисел существование предела последовательности равносильно существованию пределов соответствующих последовательностей вещественных и мнимых частей комплексных чисел. Предел (числовой последовательности) — одно из основных понятий математического анализа. Каждое вещественное число может быть представлено как предел последовательности приближений к нужному значению. Система счисления предоставляет такую последовательность уточнений. Целые и рациональные числа описываются периодическими последовательностями приближений, в то время как иррациональные числа описываются непериодическими последовательностями приближений. [1] В численных методах, где используется представление чисел с конечным числом знаков, особую роль играет выбор системы приближений. Критерием качества системы приближений является скорость сходимости. В этом отношении, оказываются эффективными представления чисел в виде цепных дробей. 7. Свойства пределов последовательности. Теорема Вейерштрасса. В математике пределом последовательности элементов пространства называют элемент того же пространства, который обладает свойством «притягивать», в некотором смысле, элементы данной последовательности. Свойство последовательности, иметь или не иметь предел, называют сходимостью: если у последовательности есть предел, то говорят, что данная последовательность сходится, в противном случае (если у последовательности нет предела) говорят, что последовательность расходится. Часто встречающимся является предел числовой последовательности. Пределом последовательности точек топологического пространства является такая точка, каждая окрестность которой содержит все элементы последовательности, начиная с некоторого номера. Все открытые, в смысле данной топологии, множества, содержащие данную точку, образуют систему окрестностей этой точки. В метрическом пространстве систему окрестностей образуют, например, все открытые шары с центром в данной точке. Поэтому свойство сходимости последовательности элементов метрического пространства к данной точке формулируется как способность «удерживать» на заданном расстоянии все точки последовательности, начиная с некоторого номера. Сходящиеся последовательности обладают следующим свойством: каждая подпоследовательность сходящейся последовательности сходится, и её предел совпадает с пределом исходной последовательности. Другими словами, у последовательности не может быть двух различных пределов.[1] Может, однако, оказаться, что у последовательности нет предела, но существует подпоследовательность (данной последовательности), которая предел имеет. Если из последовательности точек пространства можно выделить сходящуюся подпоследовательность, то, говорят, что данное пространство компактно или, точнее, секвенциально компактно. Понятие предела последовательности непосредственно связано с понятием предельной точки (множества): если у множества есть предельная точка, то существует последовательность элементов данного множества, сходящаяся к данной точке. Таким образом, у последовательности может быть несколько предельных точек, но, если последовательность сходится, то все предельные точки совпадают друг с другом и совпадают с пределом самой последовательности. Предел числовой последовательности является основным объектом рассмотрения в математическом анализе. В общей топологии рассматриваются наиболее общие свойства сходимости, а, также, вводятся и изучаются обобщения Теоре́ма Вейерштра́сса в математическом анализе и общей топологии гласит, что функция, непрерывная на компакте, ограничена на нём и достигает своей верхней и нижней грани. Пусть дана непрерывная числовая функция, определённая на отрезке, то есть 8. Предел функции. Геометрический смысл предела функции. Функция точки графика функции у=ƒ(х) лежат внутри полосы шириной 2ε, ограниченной прямыми у=А+ ε, у=А-ε (см. рис. 110). Очевидно, что величина δ зависит от выбора ε, поэтому пишут δ=δ(ε). 9. Основные теоремы о пределах Теорема 1. (о предельном переходе в равенстве) Если две функции принимают одинаковые значения в окрестности некоторой точки, то их пределы в этой точке совпадают. Теорема 2. (о предельном переходе в неравенстве) Если значения функции f(x) в окрестности некоторой точки не превосходят соответствующих значений функции g(x), то предел функции f(x) в этой точке не превосходит предела функции g(x). Теорема 3. Предел постоянной равен самой постоянной. Теорема 4. Функция не может иметь двух различных пределов в одной точке. Теорема 5. Если каждое слагаемое алгебраической суммы функций имеет предел при Теорема 6. Если каждый из сомножителей произведения конечного числа функций имеет предел при Теорема 7. Если функции f(x) и g(x) имеют предел при причем 10. Понятие бесконечно большая и бесконечно мала величина Бесконечно малая (величина) — числовая функция или последовательность, которая стремится к нулю. Если х стремится х 0 или при хстремится к бесконечности,если предел равен нулю 2. если для любого даже сколь угодно малого положительного числа е больше 0, найдется такое положительное число больше нуля, что для всех х, не равных х0 и удовлетворяющих условию. Бесконечно большая (величина) — числовая функция или последовательность, которая стремится к бесконечности определённого знака. Называется бесконечно большой величиной при х стремится к х0 ,если для любого даже сколь угодно большого положительного числа М больше 0 найдется такое положительно число б больше 0, что для всех х, не равных х0 и удовлетворяющих условию модуль х-х0 меньше б. 11. Первый замечательный предел Первый замечательный предел:
Следствия
12. Второй замечательный предел. Формы 1-го и 2-го пределов . 1. 2. 3. 4. 5. 6. 13. Непрерывность функции в точке Непрерывная функция — функция без «скачков», то есть такая, у которой сколь угодно малые изменения аргумента приводят к сколь угодно малым изменениям значения функции. Непрерывная функция, вообще говоря, синоним понятия непрерывное отображение, тем не менее чаще всего этот термин используется в более узком смысле — для отображений между числовыми пространствами, например, на вещественной прямой. Эта статья посвящена именно непрерывным функциям, определённым на подмножестве вещественных чисел и принимающим вещественные значения. Условия:1. определена в точке х0 2.имеет конечны предел функции при х->х0 3. Этот предел равен значению функции в точке х0 2) функция непрерывна в точке,если она определена в этой точке,и бесконечно малому приращению аргумента соответствует бесконечно малое приращение функции: limx-˃0 ▲y=0
|
||
|
Последнее изменение этой страницы: 2016-04-21; просмотров: 2109; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.137 (0.009 с.) |

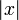 В случае вещественного Х абсолютная величина есть непрерывная кусочно-линейная функция, определённая следующим образом:
В случае вещественного Х абсолютная величина есть непрерывная кусочно-линейная функция, определённая следующим образом:
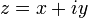 также иногда называемый абсолютной величиной[1]. Он определяется по формуле:
также иногда называемый абсолютной величиной[1]. Он определяется по формуле: 
 означает расстояние между точками
означает расстояние между точками  и
и 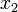 и, таким образом, может быть использована как мера близости одной (вещественной или комплексной) величины к другой.
и, таким образом, может быть использована как мера близости одной (вещественной или комплексной) величины к другой.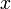 однозначно определяет значение выражения
однозначно определяет значение выражения 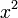 а значение месяца однозначно определяет значение следующего за ним месяца. Аналогично некоторый задуманный заранее алгоритм по варьируемым входным данным выдаёт определённые выходные данные.
а значение месяца однозначно определяет значение следующего за ним месяца. Аналогично некоторый задуманный заранее алгоритм по варьируемым входным данным выдаёт определённые выходные данные.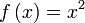
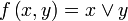
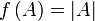

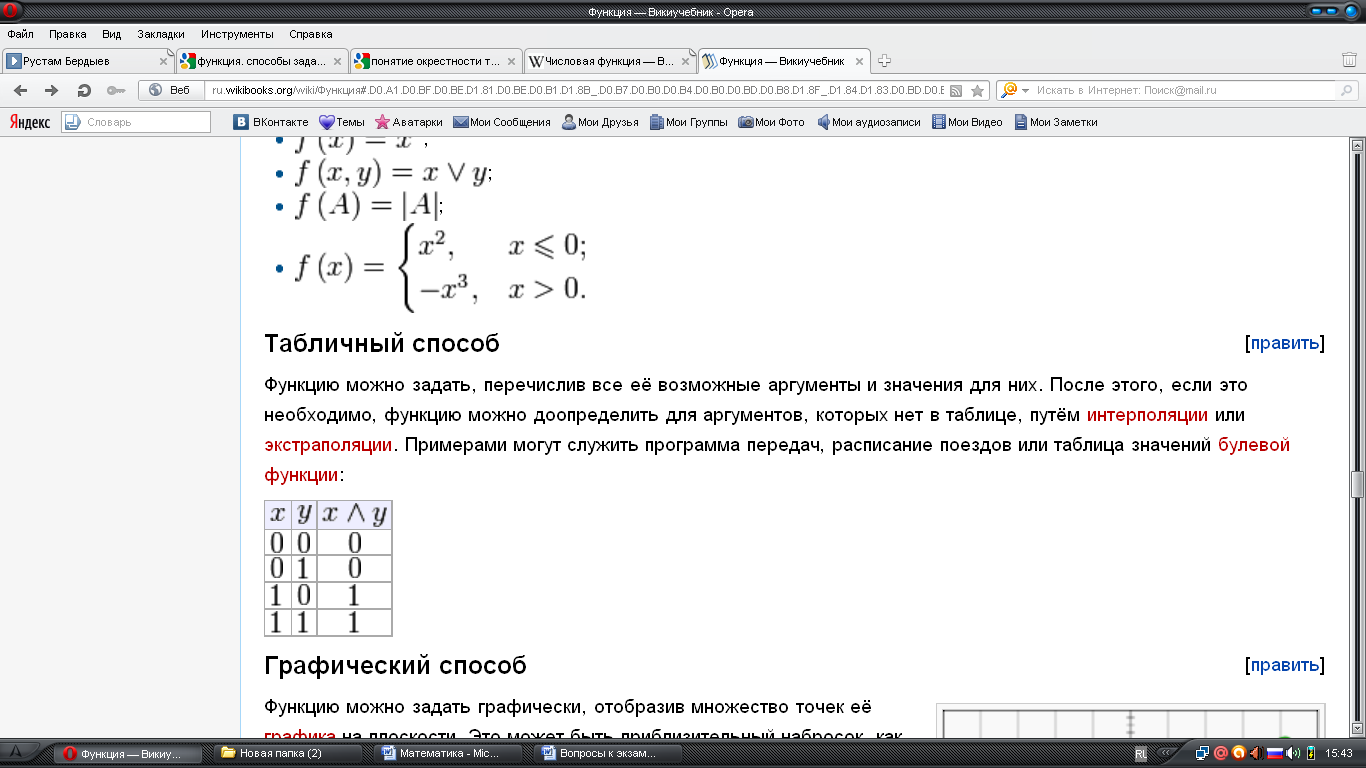
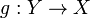 является обратной к функции
является обратной к функции 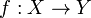 , если выполнены следующие тождества:
, если выполнены следующие тождества: 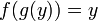 для всех
для всех 
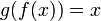 для всех
для всех 
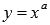
 , где
, где  ,
,  и
и 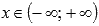
 , где
, где 
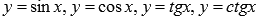

 и
и 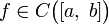 . Пусть
. Пусть  — точные верхняя и нижняя грани множества значений функции
— точные верхняя и нижняя грани множества значений функции 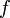 соответственно. Тогда эти значения конечны
соответственно. Тогда эти значения конечны 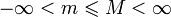 и достигаются (существуют
и достигаются (существуют 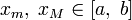 такие, что
такие, что 
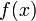 имеет предел
имеет предел  в точке
в точке 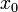 , предельной для области определения функции
, предельной для области определения функции 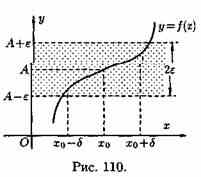
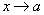 , то и алгебраическая сумма имеет предел при
, то и алгебраическая сумма имеет предел при 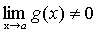 , то и их частное имеет предел при
, то и их частное имеет предел при 


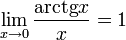

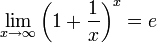 или
или 
 Следствия
Следствия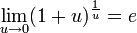
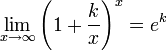
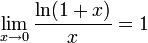
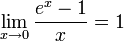
 для
для  ,
,