
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Теоремы о непрерывных функциях.Содержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
Определение 22.1: (Условие Коши) Функция
Теорема 1: (Критерий Коши) Для того, чтобы функция Теорема 2: Непрерывная на отрезке функция ограничена на нём. Теорема 3: Непрерывная на отрезке функция достигает на нём своего максимального и минимального значения. (Дать определение Теорема 4: Пусть
Теорема 5: Пусть
Определение 22.2: Функция называется возрастающей (убывающей) в точке, если существует такая окрестность этой точки, в которой данная функция является возрастающей (убывающей). Теорема 6: Если функция Определение 22.3: Непрерывная на множестве Определение 22.4: Непрерывная на множестве Замечание: Точки минимума и максимума функции называют точками экстремума данной функции. Теорема 7: (Ферма, необходимое условие экстремума) Если функция Замечание: Точки, в которых производная функции равна нулю мы будем называть стационарными точками этой функции. Теорема 8: (Ролля) Если функция Теорема 9: (Лагранжа) Если функция Теорема 10: (Коши) Пусть функции Теорема 11: Пусть Теорема 12: (Правило Лопиталя)
15. Точки разрыва функции и их классификация Если функция f (x) не является непрерывной в точке x = a, то говорят, что f (x) имеет разрыв в этой точке. На рисунке 1 схематически изображены графики четырех функций, две из которых непрерывны при x = a, а две имеют разрыв.
Классификация точек разрыва функции Все точки разрыва функции разделяются на точки разрыва первого и второго рода. Говорят, что функция f (x) имеет точку разрыва первого рода при x = a, если в это точке
При этом возможно следующие два случая:
Такая точка называется точкой устранимого разрыва.
Такая точка называется точкой конечного разрыва. Модуль разности значений односторонних пределов Функция f (x) имеет точку разрыва второго рода при x = a, если по крайней мере один из односторонних пределов не существует или равен бесконечности. 16. Понятие производной функции и ее геометрический смысл Опр. Производная есть предел отношения приращения функции к приращению аргумента. (Коши 1820 г.) Функция, имеющая производную в некоторой точке x наз. дифференцируемой в этой точке. Операция нахождения производной наз. дифференцированием. Геометрический смысл производной: тангенс угла наклона касательной. На графике функции y = f(x) имеем точки M 0(x0,y0) и M (x;y). Прямая М0Мназ. секущей и пересекает ось Ох под углом
При х lim tg х
17. Теорема о непрерывности дифференцируемой функции. Теорема 1. Пусть функция y = f(x) дифференцируема на интервале (a, b). Тогда функция f непрерывна на (a, b). Доказательство: Возьмем произвольное фиксированное число x Но тогда Правила дифференцирования Если с - постоянное число, и u = u(x), v = v(x) - некоторые дифференцируемые функции, то справедливы следующие правила дифференцирования: 1) (с) ' = 0, (cu) ' = cu'; 2) (u+v)' = u'+v'; 3) (uv)' = u'v+v'u; 4) (u/v)' = (u'v-v'u)/v2; 5) если y = f(u), u = j(x), т.е. y = f(j(x)) - сложная функция, или суперпозиция, составленная из дифференцируемых функций j и f, то
20. Производная от сложной функции.
где u = g(x) - внутренняя функция, являющаяся, в свою очередь, аргументом для внешней функции f.
Данная формула показывает, что производная сложной функции равна произведению производной внешней функции на производную от внутренней функции. Важно, однако, что производная внутренней функции вычисляется в точке x, а производная внешней функции - в точке u = g(x)! 21. Понятие экстремумов функций.
|
||||||||||||
|
Последнее изменение этой страницы: 2016-04-21; просмотров: 1631; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.223.172.110 (0.011 с.) |

 удовлетворяет в точке
удовлетворяет в точке  условию Коши, если:
условию Коши, если: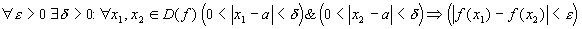
 )
) , причём
, причём  , тогда:
, тогда:

 и
и  , то эта функция возрастает (убывает) в данной точке.
, то эта функция возрастает (убывает) в данной точке. функция
функция  глобальный минимум (максимум), если:
глобальный минимум (максимум), если: 

 и достигает в ней экстремального значения, то:
и достигает в ней экстремального значения, то:  .
. , то:
, то:  .
. . Дайте геометрическую интерпретацию этой теоремы.
. Дайте геометрическую интерпретацию этой теоремы. непрерывны и дифференцируемы на
непрерывны и дифференцируемы на  , тогда:
, тогда:  .
. и
и  , тогда:
, тогда:  .
. точки
точки  , за исключением, быть может, самой точки
, за исключением, быть может, самой точки  . Тогда:
. Тогда: 
 .
.
 и правосторонний предел
и правосторонний предел  ;
;

 называется скачком функции.
называется скачком функции.
 tg
tg  х0 секущая становится касательной
х0 секущая становится касательной
 (a,b).. По условию теоремы
(a,b).. По условию теоремы  Следовательно, в малой окрестности числа x0 можно определить функцию α = α(Δx), стремящуюся к нулю при
Следовательно, в малой окрестности числа x0 можно определить функцию α = α(Δx), стремящуюся к нулю при  такую, что
такую, что 
 и, следовательно, функция f непрерывна при x = x0. Так как число x0 – произвольное, то функция f непрерывна на всем интервале (a, b).
и, следовательно, функция f непрерывна при x = x0. Так как число x0 – произвольное, то функция f непрерывна на всем интервале (a, b). , или
, или  .6) если для функции y = f(x) существует обратная дифференцируемая функция x = g(y), причем
.6) если для функции y = f(x) существует обратная дифференцируемая функция x = g(y), причем  ≠ 0, то
≠ 0, то  .
.
 также дифференцируема по x и ее производная равна
также дифференцируема по x и ее производная равна



