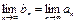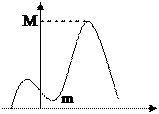Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Вопрос 18. Непрерывность суммы произведения и частного в непрерывной функции.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Если функции f(x) и g(x) непрерывны в точке х0, то их сумма, произведение и частное(если g(x0)≠0) являются функциями, непрерывными в точке х0. Доказательство: Покажем непрерывность частного. Пусть f(x),g(x) непрерывны в точке х0, т.е. По теореме об арифметических действиях с пределами существует
Вопрос 19. Непрерывность элементарной функции в области определения. Теорема: Все элементарные функции непрерывны в области определения. Непрерывность рациональных функций: 1. Постоянная функция y(х) = C = const, очевидно, непрерывна в любой точке (предел постоянной функции равен этой постоянной в любой точке). 2.Функция y(х)= х непрерывна в любой точке х (для "e>0 возьмём d = e, тогда если | х- х0|<d, то | f(х)- f(х0)| = | х- х0|<e=d). 3.Функция y(х)= х2 непрерывна в любой точке х как произведение двух непрерывных функций. 4.По индукции функция y(х)= хn = хn-1 х непрерывна в любой точке х как произведение двух непрерывных функций. По той же причине непрерывна функция y(х)= аnхn, где аn=C=const. 5.Рациональная функция Непрерывность дробно-рациональных функций: 1) Непрерывность показательной функции y=ax, a>0,a≠1. Требуется доказать, что Непрерывность логарифмической функции Непрерывность тригонометрических функций: а. y=sinx. sinx-sinx0
при х ® х0 (мы воспользовались неравенством |sin х |£| х|). б. в. Функции y=tgx и y=ctgx непрерывны в точках, в которых они определены, как частное непрерывных функций. Вопрос 20. Непрерывность функции справа и слева в точке разрыва функции и их классификации. Функция f(x) называется непрерывной в точке х0 слева, если Функция f(x) называется непрерывной в точке х0 справа, если Если одно из этих условий не выполнено, то функция f(x) имеет в точке х0 разрыв, соответственно, слева или справа. Классификация точек разрыва. Разрывы первого рода: Пусть существует левый предел а и правый предел b и a≠b, тогда у функции разрыв первого рода типа конечного скачка.
a≠b
Если один из односторонних пределов равен ∞, то говорят, у функции разрыв второго рода типа бесконечного скачка.
Вопрос 21. Теорема о сохранении знаков непрерывной функции. Пусть функция f(x) непрерывна в точке x0 и f(x)≠0, тогда сущее. окрестность этой точки, в которой функция сохраняет знак. Доказательство: Пусть для определенности f(x0)>0, т.к.
f(x0) можно сделать положительным за счет выбора числа ε.
x ∈(x0- ε);x0+ ε)
Вопрос 22. Теорема о нуле непрерывной функции и промежуточном значении. 1) Пусть функция f(x) непрерывна на сегменте [a;b], и на концах его принимает значение разных знаков, тогда обязательно найдется такая точка С внутри [a;b], в которой функция обращается в 0. [a;b] x∈[a;b] f(c)=0
Разделим [a;b] пополам: 1)Пусть f(c)=0 2) f(c)≠0 На концах из каждого-то из 2х полученных отрезках функция принимает на его концах разные знаки. [a1;b1] вновь разделим пополам. Опять выбираем тот отрезок, на концах которого функция принимает значение разных знаков [a2;b2] и опять разделим пополам. Длина отрезка Левые концы отрезка a1, а2, …аn – образуют возрастающую последовательность, но ограничены всегда числом b. По теореме о монотонной последовательности Правые концы отрезков образуют монотонно убывающую последовательность, но всегда ограничены числом а. По теореме о монотонной последовательности Т.к.
По теореме о сохранении знака непрерывной функции с одной стороны f(an)<0 => f(c)<0; f(bn)>0 => f(c)>0 => f(c)=0. 2)Если непрерывная функция принимает два значения, то она принимает и любое значение между ними.
2) Пусть функция f(x) непрерывна на [a;b], тогда она ограничена на этом отрезке,
|
|||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 1638; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.119.253.53 (0.008 с.) |

 ,
, 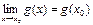 , причем g(x0)≠0.
, причем g(x0)≠0.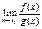 , и этот предел равен
, и этот предел равен , что означает непрерывность функции
, что означает непрерывность функции 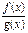 в точке х0.
в точке х0. непрерывна в любой точке х как сумма непрерывных функций.
непрерывна в любой точке х как сумма непрерывных функций.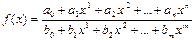 непрерывна в любой точке х, в которой знаменатель отличен от 0, как частное непрерывных функций.
непрерывна в любой точке х, в которой знаменатель отличен от 0, как частное непрерывных функций. . Рассмотрим разность
. Рассмотрим разность 
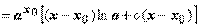 . Эта разность - БМ функция при х® х0, следовательно, ах®
. Эта разность - БМ функция при х® х0, следовательно, ах® 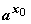 при при х® х0
при при х® х0 . По формуле эквивалентных БМ
. По формуле эквивалентных БМ  ~
~ 
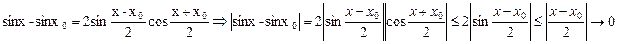
 непрерывна как суперпозиция непрерывных функций.
непрерывна как суперпозиция непрерывных функций.


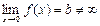



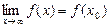 , то
, то  .
.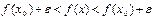

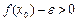
 f(x)>0
f(x)>0
 Для разрывной функции это не будет справедливо.
Для разрывной функции это не будет справедливо. Доказательство:
Доказательство:
 существует.
существует. существует.
существует.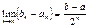 , то
, то