
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Вычисление длины дуги кривойСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Как можно задать кривую на плоскости? а) явное задание у=у(х), а≤x≤b y=4x+5 y=x2-5x+6
в) полярные координаты
α≤φ≤β r≥0 0≤φ≤2π
Установим связь декартовых и полярных координат Построим: (x2+y2)=4(x2-y2) 1) x=rcosφ y=rsinφ
r4=4r2(cos2φ-sin2φ)
r2=4rsinφ cosφ=π В пространстве кривую можно задать только параметрически.
Найдем производную параметрически заданной функции.
1.y=y(x)-исключим t 2.y(t)=y(x(t)) Продифференцируем 2-е выражение, тогда
Опр.1 Кривая называется гладкой, если в каждой ее точке можно провести касательную, направление которой непрерывно изменяется. Опр.2. Кривая называется стремящейся, если она имеет конечную длину. Что понимается под длиной прямой? 1) Возьмем прямую, впишем в нее ломаную, число звеньев которой будет увеличиваться.
Li- дина каждого звена
Конечный предел суммы при х→0 называется длиной кривой. ∆хi→0 Тогда мы видим, что сумма Сумма Следовательно, длина кривой вычисляется:
2) Выведем длину кривой в случае параметрического задания
3) Прямая задана в полярных координатах. r=r(t)
Площадь криволинейной трапеции
Если фигура ограничена сверху кривой y=f(x), снизу кривой y=g(x), слева и справа-отрезками прямых х=а и х=b, то ее площадь равна:
Площадь сектора
Вопрос 60.Числовые ряды Числовым рядом называется сумма Вопрос 61. Сумма числового ряда Сумма n первых членов ряда Sn= a1+a2+…+an называется n-й частичной суммой ряда. Суммой ряда называется предел частичных сумм Исследование числового ряда сводится к сводимости последовательностей частных сумм: Вопрос 62.Сходимость числового ряда Ряд называется сходящимся, если существует конечный предел последовательности его частичных сумм, т.е. Если конечного предела последовательности частичных сумм не существует, то ряд называется расходящимся. Вопрос 63.Необходимое условие сходимости - Необходимое условие сходимости: Если ряд сходится, то предел его общего члена an при n→∞ равен нулю, т.е. (Для того, чтобы ряд сходился, необходимо, чтобы его общий член стремился к 0. Доказательство: т.к. ряд сходится,то
Гармонический ряд,у которого суммы нет. Вопрос 64. Признаки сходимости положительных рядов(признаки сравнения Коши,Даламбера) Знакоположительные ряды.
Послеовательность частичных сумм монотонно возрастает, поэтому по теорем о сходимости монотонной последовательности для существования предела, необходимо и достаточно, чтобы последовательность частичных сумм была огранична.
Тогда Достаточные признаки: Пусть существует ряд an и bn и выполняется неравенство an≤bn => если ряд bn сходится, то an тоже сходится. Если ряд an расходится, то bn тоже. Доказательство: Sna –ряд сходимости суммы an. Sna =a1+a2+…+an≤b1+b2+…+bn. Рассмотрим случай 1.
По критерию сходимости дя знака положительных рядов существует конечный предел. Случай 2.
a1+a2+…+an→+∞, отсюда b1+b2+…+bn.→+∞
α>1- ряд сходится α≤1- ряд расходится
Признак Коши. Пусть существует предел 1)q<1- ряд сходится 2)q>1-ряд расходится 3)q=1- ничего сказать нельзя(признак не работает) Доказательство: Для любого положения числа ε(∀ε>0) мы имеем 1) q<1
т.к. ε – любое число, его можно взять таким, что q+ε=q1<1 an<a1n
2) q>1 За счет выбора ε можно q-ε>1 q-ε=q2 qn>q2n – расходится Признак Даламбера. Пусть существует 1)q<1 –ряд сходится 2)q>1-ряд расходится 3) q=1- нужны дополнительные сведения. Доказательство: (∀ε>0)
1) q<1, также за счет выбора ε можно q+ε=q<1 an+1<anq1<an-1q2...<a1qn но
2) q>1 аналогично, как признак Коши.
|
||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 646; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.224.73.150 (0.01 с.) |

 б) параметрическое задание
б) параметрическое задание



 r=r(φ)
r=r(φ) ,,
,, cos2φ≥0
cos2φ≥0


 2)x2+y2=4y
2)x2+y2=4y





 - так вычисляется производная параметрически заданной функции.
- так вычисляется производная параметрически заданной функции.


 , если кривая гладкая.
, если кривая гладкая. принимает вид
принимает вид 
 есть интегрированная сумма для функции
есть интегрированная сумма для функции 







 , an- общий член ряда.
, an- общий член ряда. , если S≠∞, ряд называется сходящимся.
, если S≠∞, ряд называется сходящимся.


 и
и 

 - расходится.
- расходится. 


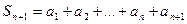



 всегда существует и относителен от ∞.
всегда существует и относителен от ∞. сходится => его Snb≤M. Т.е. частичные суммы ограничены => Sna также ≤M
сходится => его Snb≤M. Т.е. частичные суммы ограничены => Sna также ≤M - расходится, Sna =∞
- расходится, Sna =∞

 , тогда:
, тогда:

 - это геометрическая прогрессия со знаком <1 => сходится, поэтому по признаку сравнения исходный ряд сходится.
- это геометрическая прогрессия со знаком <1 => сходится, поэтому по признаку сравнения исходный ряд сходится. 
 , тогда
, тогда
 - сходится => исходный ряд тоже сходится.
- сходится => исходный ряд тоже сходится.


