
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Вопрос 51. Определение определенного интегралаСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Разобьем сегмент [a;b] произвольно точками деления. x0=a, x1,x2,…xn=b ∆xi=xi-xi-1 Выберем на участке [xi;xi+1] произвольную точку Сi. Составим сумму Определение: Предел интегрированных сумм при λ→0 называется определенным интегралом, а функция y=f(x) называется интегрированной на сегменте [a;b]
В определении определенного интеграла: 1) Произвольное разбиение 2) Произвольный выбор точки Сi Рассмотрим геометрический смысл определенного интеграла: Определение: Назовем криволинейной трапецией фигуру, которую образована прямыми x=a,x=b,y=0,y=b(x). Выясним смысл слагаемого в интегральной сумме каждое слагаемое есть площадь прямоугольника со сторонами (∆xi;f(ci)) при λ→0 эти S→S криволинейной трапеции. Т.к. в определении определенного интеграла предел должен быть конечным, то необходимо, чтобы функция y=f(x) на отрезке [a;b]была ограниченной, т.е. ƎM>0,
Теорема: Все непрерывные функции на [a;b]интегрируемы на этом отрезке. y=f(x)-непрерывна на [a;b]=> Вопрос 52.Свойства неопределенного интеграла
Данные свойства вытекают из свойств предела функции. Докажем свойство 3.
Найдем предел интегрированной суммы.
Свойства, связанные с неравенствами:
Свойство 3 вытекает из свойства 2.
Определение: Назовем средним значением функции на [a;b] величину m≤fcp≤M Если f(x) непрерывна, то по свойству непрерывной функции это значение fср. примется функцией в некоторой точке С ∈ (a;b) Поэтому докажем важную теорему о среднем:
Вопрос 53.Интегрируемость непрерывной функции Если функция f (x) непрерывна на отрезке [a, b], то она интегрируема на нем. Вопрос 54. Интеграл с переменным верхним пределом Пусть y=f(x) интегрируема на [a;b]
Теорема: Если функция f(x) непрерывна на [a;b], то функция F(x) также непрерывна на [a;b] Доказательство:
Составим приращение:
Тогда по теореме о среднем:
Устремим ∆x→0:
аргумента соответствует бесконечно малое приращение функции)
Вопрос 55. Существование первообразной для непрерывной функции.
Теорема: Пусть функция f(x) непрерывна на [a;b] тогда F(x)- дифференцирована на [a;b] и справедлива формула: Т.е F(x) является первообразной для функции f(x). Доказательство: Составим разностное отношение
Перейдем к пределу при х→0
с→х F’(x)=f(x) Вопрос 56.Формула Ньютона-Лейбница Пусть функция y=f(x) непрерывна на отрезке [a;b] и F(x)- любая первообразная для f(x) на [a;b]. Тогда определенный интеграл от функции f(x) на [a;b] равен приращению первообразной F(x) на этом отрезке, т.е. Доказательство: F’(x)=f(x)
Пример:
Вопрос 57. Замена переменной в определенном интеграле. Теорема: Пусть функция φ(t) имеет непрерывную производную на отрезке [a;b], а= φ(α), b= φ(β) и функция f(x) непрерывна в каждой точке х вида х= φ(t), где t∈ (a;b). Тогда справедливо следующее равенство:
Пусть F(x) и Ф(t) — некоторые первообразные для функций f (x) и f (φ (t))·φ ' (t). Доказано, что F (φ (t)) также является первообразной для функции f (φ (t))·φ ' (t). Тогда найдется такое число С, что Ф(t) = F(φ (t)) + C, где t ∈ [ α, β]. Следовательно, Ф(β) - Ф(α) = F(φ (β)) + C - (F(φ (α)) + C) = F(b) - F(a). Использование замены переменной позволяет упростить интеграл, приблизив его к «табличному». При этом в отличие от неопределенного интеграла, в данном случае нет необходимости возвращаться к исходной переменной интегрирования. Достаточно лишь найти пределы интегрирования α и β по новой переменной t как решение относительно переменной t из уравнений φ (t) = a и φ (t) = b. Вопрос 58.Интегрирование по частям в определенном интеграле. Пусть функции u=u(x) и υ=υ(х) имеют непрерывные производные на отрезке [a;b], тогда: Формула интегрирования по частям для определенного интеграла:
u- должно упроститься υ- легко интегрироваться Поскольку (uυ)’=u’υ+uυ’, то функция uυ является первообразной для функции u’υ+uυ’. Тогда, по формуле Ньютона-Лейбница получаем:
Вопрос 59.Геометрические приложения определенного интеграла(вычисление площади, вычисление длины дуги кривой)
|
|||||||||||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 545; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.110.21 (0.01 с.) |

 Пусть задана функция y=f(x) на отрезке [a;b].
Пусть задана функция y=f(x) на отрезке [a;b].
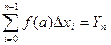 ,
, 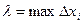
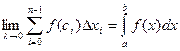 -конечный предел
-конечный предел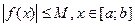
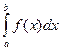 - существует.
- существует.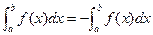
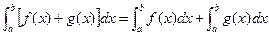
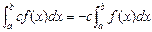

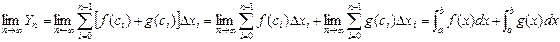
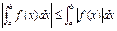
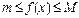
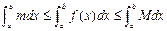
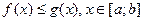
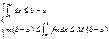
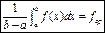
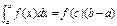
 , где xi[a;b] называется интегралом с переменным верхним пределом.
, где xi[a;b] называется интегралом с переменным верхним пределом.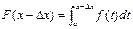 ,
,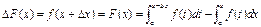
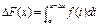
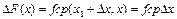
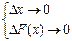 - а это определение непрерывности функции(бесконечно малому приращению
- а это определение непрерывности функции(бесконечно малому приращению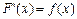 .
.
 , где
, где 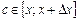
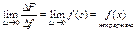
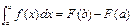 .
.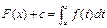

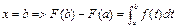
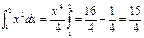
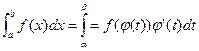
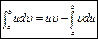 , где
, где 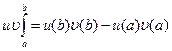
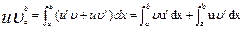 , что равносильно
, что равносильно 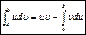 , т.к. по определению дифференциала u’(x)dx=du и υ’(x)dx=dυ
, т.к. по определению дифференциала u’(x)dx=du и υ’(x)dx=dυ


