
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Вопрос 38. Исследование функции на выпуклость.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Пусть y=f(x) дифференцируема на отрезке (a;b), т.е. в каждой точке х ∈ (a;b) можно провести касательную Определение 1. Функция называется выпуклой вниз, если для всех х из интервала [a;b] график
Достаточное условие выпуклости: Теорема1. Пусть функция y=f(x) на участке (a;b) имеет вторую производную, тогда f’’(x)>0, то функция выпуклая вниз, если f’’(x)<0, то функция выпуклая вверх. Доказательство: Пусть f’’(x)>0; x∈ (a;b) обозначим с∈ (a;b) Запишем уравнение касательной, проходящей через точку С; у- ордината касательной. У-f(c)=f’(c)(x-c) Для функции y=f(x) запишем формулу Тейлора в окрестности точки С.
Найдем разность между точками прямой:
Определение 3. Точкой С называется точка перегиба функции, в окрестности которой функция меняет выпуклость.
Теорема3. Пусть вторая производная в точке С=0 и в окрестности этой точки меняет знак тогда в этой точке будет перегиб.
Схема исследования функции на выпуклость и наличие точек перегиба: 1) Находим вторую производную функции f’’(x) 2) Находим точки, в которых вторая производная f’’(x)=0 или не сущетвует. 3) Исследуем знак второй производной слева и справа от найденных точек и делаем вывод об интервалах выпуклости и наличии точек перегиба. 4) Находим значение функции в точках перегиба. Вопрос 39. Асимптоты графика функции. Асимптотой графика функции y=f(x) называется прямая, обладающая таким свойством, что расстояние от точки (x,f(x)) до этой прямой стремится к 0 при неограниченном удалении точки графика от начала координат. Существует вертикальная, горизонтальная и наклонная асимптоты. 1)Пусть функция определена в некоторой окрестности точки x0 и хотя бы один из пределов функции при х→х0 -0(слева) или при х→х0 +0(справа) равен бесконечности, т.е. Пусть функция определена при достаточно больших х и существует конечный предел функции Пусть функция определена при достаточно больших х и существуют ее конечные пределы Уравнения возможной асимптоты:
1) Если к=0, то функция имеет горизонтальную асимптоту.
2) Пусть при х→а f(x)→∞, тогда прямая х=а называется вертикальной асимптотой. Вопрос 40. Исследование функции и построение графика. 1)Находим область определения функции 2) Исследуем функцию на четность-нечетность.
3) Ищем точки пересечения с осями координат 4) Интервалы монотонности функции 5) Находим асимптоты графиков 6) Находим интервалы выпуклости функции и точки перегиба 7) Построение графика функции Вопрос 41. Функции двух переменных. Область определения. Функция 2х переменных обозначается: z=f(x;y) Тогда ее область определения Х есть подмножество координат плоскости Оху.
Каждой точке из области определения поставлено по определенному закону z. (x,y) ∈Д→z∈R Любой функции z=f(x;y) можно поставить в соответствие две функции одной переменной: при фиксированном значении х=х0 функцию z=f(x0;y) и при фиксированном значении у=у0 функцию z=f(x;y0). Их вид может отличаться. Графиком функции двух переменных z=f(x;y) называется множество точек трехмерного пространства (x;y;z). График функции двух переменных z=f(x;y) представляет собой некоторую поверхность в трехмерном пространстве. Для построения графика функции z=f(x;y) полезно рассматривать функции одной переменной z=f(x;y0) и z=f(x0;y), представляющие сечения поверхности z=f(x;y) плоскостями, параллельными координатным плоскостям Oxz и Oyz.
Пример:
О.Д.З.:
1)
2)
1. z=x2 +y2 (параболоида) 2. z2=x2 +y2, z>0 (Коническая поверхность) 3. x2 +y2 +z2=R2 (сфера) 4.
|
|||||||||||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 516; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.54.210 (0.006 с.) |

 функции лежит выше касательной.
функции лежит выше касательной. Определение 2. Функция называется выпуклой вверх, если на данном интервале ее график лежит выше касательной
Определение 2. Функция называется выпуклой вверх, если на данном интервале ее график лежит выше касательной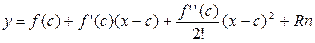

 => y>Y
=> y>Y Теорема2 Пусть функция дважды дифференцируема, тогда для того, чтобы точка С была точкой перегиба, необходимо, чтобы вторая производная в этой точке =0.
Теорема2 Пусть функция дважды дифференцируема, тогда для того, чтобы точка С была точкой перегиба, необходимо, чтобы вторая производная в этой точке =0.
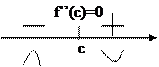
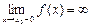 или
или 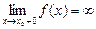 . Тогда прямая х=х0 является вертикальной асимптотой графика функции.
. Тогда прямая х=х0 является вертикальной асимптотой графика функции. . Тогда прямая y=b есть горизонтальная асимптота графика функции.
. Тогда прямая y=b есть горизонтальная асимптота графика функции.
 . Тогда прямая y=kx+b является наклонной асимптотой графика функции.
. Тогда прямая y=kx+b является наклонной асимптотой графика функции.


 - четная, график симметричен относительно ОУ
- четная, график симметричен относительно ОУ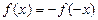 - нечетная, график симметричен относительно начала координат.
- нечетная, график симметричен относительно начала координат.


 или
или 




 (эллипсоид)
(эллипсоид)


