
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Определение предела функции в точке по Гейне.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Число A называется пределом функции f(x) в точке x=
Сравнение бесконечно малых величин. Порядок малости. Функция α(х) называется б.м. функцией при х -> a (или в окрестности точки а),если limα(x)=0. x->a Две б.м. α и β называются бесконечно малыми одного порядка, если предел их отношения равен некоторому числу, отличному от нуля, т.е. если lim(α/β)=A ≠ 0. x->a Две б.м. α и β называются эквивалентными если предел их отношения равен 1, т.е.: lim(α/β)=1 α~β x->a
Если lim(α/β)=0 (a lim(β/α)=∞), то α называется б.м. высшего порядка малости по x->a x->a сравнению с бесконечно малой β, напротив,β называется при этой бесконечно малой низшего порядка малости по сравнению с α. Бесконечно малая α называется б.м. к-го порядка по отношению к б.м. β, если α и βк будут бесконечно малыми одного порядка, т.е. lim (α/βk)=A ≠ 0. x->a Если отношение α/β при x->a не стремится ни к какому пределу; ни к конечному, ни к бесконечному, то говорят, что б.м. α и β несравнимы между собой.
Таблица э.м.ф. 1) sinα(x)~α(x) 2) tgα(x)~α(x) 3) 1 – cosα(x)~ 4) arcsinα(x)~α(x) 5) arctgα(x)~α(x) 6) ln(1+α(x))~α(x) 7) eα(x)-1~α(x) 8) (1+
Определение функции, непрерывной в точке, по Коши. Функция f(x), определённая в некоторой окрестности точки х0 называется непрерывной в точке х0 если
Функция f(x) называется непрерывной в точке х0, предельной для области определения этой функции, если для любого наперед заданного числа Определение функции, непрерывной в точке, на языке приращений Пусть y=f(x) непрерывна в точке
Функция y=f(x) называется непрерывной в точке приращению аргумента соответствует бесконечно малое приращение функции.
Точки разрыва и их классификации. Если в какой-либо точке х0 функция не является непрерывной,то точка х0 называется точкой разрыва функции, а сама функция разрывной в этой точке. Различают 2 вида точек разрыва: точки разрыва первого рода и точки разрыва второго рода. Если в точке разрыва х0 существуют конечные односторонние пределы функции, то разрыв функции называется разрывом первого рода. Если при этом f(x0-0)=f(x0+0) f(x0-0) f(x0 +0)-f(x0-0) называется скачком функции f(x) в точке х0. Понятие дифференциала. Геометрический смысл дифференциала. Дифференциал функции в некоторой точке – главная линейная часть приращения функции, равная произведению производной этой фунции в выбранной точке на приращение независимой переменной Геометрически дифференциал равен приращению ординаты касательной, проведенной к графику функции в точке хо. Производная же численно равна угловому коэффициенту касательной. Рассмотрим ^М0КN: tga=NK/M0N =>f’(x0)= NK/ равен приращению, которое получает касательная, проведенная в точке М0, соответствующая приращению ^x
12 Формула Тейлора (Маклорена) с остаточным членом в форме Пеано. Если y=f(x) определена и n-раз дифференцируема в
rn (x)=o((x-x0)n)
где rn (x)=o((x-x0)n) - остаточный член в форме Пеано. Если взять в формуле Тейлора x0 = 0, то мы получим формулу Маклорена с остаточным членом в форме Пеано
Понятие предела ФНП Пусть функция z = f (M) определена на множестве D, M (x 1, x 2,…, x n) Î Rn, M 0(x 10, x 20,…, x n0). Определение. ( По Коши ) Число А называют пределом функции z = f (M) в точке М 0 (при M ® M 0), если " e > $ d >такое, что" M Î D, удовлетворяющей неравенству0 <r(M,M0)<d, выполняется неравенство |f (M) - A|<e.
Понятие частной производной ФНП. Геометрический смысл Величина
|
||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 581; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.108 (0.006 с.) |

 , если для любой сходящейся к
, если для любой сходящейся к  последовательности
последовательности  значений аргумента х, отличных от
значений аргумента х, отличных от 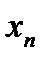 ) сходится к числу А.
) сходится к числу А.



 (a>0)
(a>0) )
) -1~
-1~ 
 \
\
 >0,существует такое
>0,существует такое 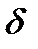 >0,что для всех значений х из области определения f(x), для которых
>0,что для всех значений х из области определения f(x), для которых  <
< 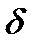 выполняется неравенство
выполняется неравенство  <
<  .
. и существует
и существует  ,
, - бесконечно малая, при
- бесконечно малая, при  , то
, то 
 - это приращение функции.
- это приращение функции. - приращение аргумента.
- приращение аргумента. , если эта функция определена в какой-нибудь окрестности точки
, если эта функция определена в какой-нибудь окрестности точки 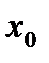 и если
и если 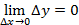 , т.е. если бесконечно малому
, т.е. если бесконечно малому f(x0), то х0 – точка устранимого разрыва, если
f(x0), то х0 – точка устранимого разрыва, если f(x0+0), то х0 – точка неустранимого разрыва первого рода, а разность
f(x0+0), то х0 – точка неустранимого разрыва первого рода, а разность x, NK= f’(x0)*
x, NK= f’(x0)* 
 , то можно записать:
, то можно записать: Остаточный член в форме Пеано
Остаточный член в форме Пеано Теорема. Если функция f(x) определена и n раз дифференцируема в окрестности точки x0, то при x ® x0 имеет место формула
Теорема. Если функция f(x) определена и n раз дифференцируема в окрестности точки x0, то при x ® x0 имеет место формула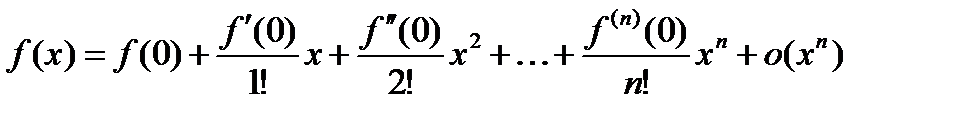


 называется частной производной от функции u=f (x 1, x 2,…, x n) по i -ой переменной и обозначается символом
называется частной производной от функции u=f (x 1, x 2,…, x n) по i -ой переменной и обозначается символом  или символом
или символом  .
.


