
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Вопрос 23. Теорема об ограниченной функции на отрезке.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Доказательство. Функция f (х) ограничена на промежутке [ а, b ], если существуют такие конечные числа m и M, что m ≤ f (х) ≤ М при a ≤ x ≤ b. Допустим, что функция f (х) при изменении х в промежутке [ а, b ] оказывается неограниченной. В таком случае для каждого натурального числа n найдётся в промежутке [ а, b ] такое значение х = х n, что f (xn) ≥ n. Однако по лемме Больцано – Вейерштрасса из этой ограниченной последовательности { x n} можно выделить сходящуюся частичную подпоследовательность:
Причем, очевидно, х 0
Однако, в силу f (xn) ≥ n имеем
Полученное противоречие и доказывает теорему. Вопрос 24. Теорема о достижении наибольшего и наименьшего значений функции. Если функция f(x) непрерывна на [a,b],то она достигает на этом отрезке наименьшего значения m и наибольшего значения М, так что m≤f(x)≤M для всех х на [a;b] Вопрос 25. Понятие производной функции в точке + таблица производных.
tgφ →tgα tgα- есть производная f’(x0)
Таблица производных:
Вопрос 26. Физический и геометрический смысл производной Из задачи о касательной следует геометрический смысл производной: производная f’(x0) есть угловой коэффициент (тангенс угла наклона) касательной, проведенной к кривой y=f(x) в точке х0, т.е. k=f’(x0). Следовательно, уравнение касательной к кривой y=f(x) в точке x0 примет вид y-f(x0)=f’(x0)(x-x0). Из задачи о скорости движения следует физический смысл производной: производная пути s’(t0) есть скорость точки в момент t0: υ(t0)=s’(t0). Если у(х) – расстояние, х- время, ∆у(∆х) –скорость, то производная есть мгновенная скорость к данному времени. Вопрос 27. Уравнение касательной Предельное положение секущей ab, когда b по кривой стремится к a называется касательной. Таким образом касательная к кривой в точке х0 есть tg угла наклона этой касательной. Поэтому уравнение касательной к кривой имеет вид: Вопрос 28. Дифференциал функции и его геометрический смысл. Функция называется дифференцируемой в точке х0, если ее приращение может быть представлено в виде:
Главная относительная ∆x часть приращенной функции, отличающаяся от этого приращения на бесконечно малую величину называется дифференциалом функции.
∆x=dx С геометрической точки зрения дифференциал есть приращение ординаты касательной. Теорема: Для того, чтобы функция была дифференцируема в точке х0 необходимо и достаточно, чтобы в этой точке существовала производная. Доказательство: - необходимость Пусть функция дифференцируема в точке, тогда Разделим данное выражение на ∆x и перейдем к пределу к ∆x→0.
- Достаточность Пусть существует f’(x0)
Из свойств предела следует
Понятие дифференцируемости и производной в точке х0 – тождественно. Связь непрерывности и дифференцируемости: Пусть функция дифференцируема в точке, тогда она не прерывна в этой точке. Из дифференцируемости всегда следует непрерывность. Из непрерывности дифференциирумость следует не всегда. Вопрос 29. Применение производной для приближенных вычислений. Пусть u(x) и υ(x) дифференцируемы, тогда справедливы следующие правила:
При малых ∆х приращение функции можно заменять ее дифференциалом. Из формулы ∆y=dy следует формула приближенного вычисления:
Вопрос 30. Теорема Ролля Пусть функция f(x) дифференцируема внутри интервала (a;b)- непрерывна на сегменте и на f(a)=f(b) (на концах отрезка принимает равные значения)найдется такая точка, в которой производная равна 0. f’(c)=0 c ∈ (a;b) Геометрический смысл теоремы: Найдется хотя бы одна точка, в которой касательная к графику функции будет параллельна оси абсцисс; в этой точке производная и будет равняться 0. Проиллюстрируем эту теорему геометрически:
f’(x)=0
f(x)- не является константой. f(x)≠f(a) Пусть f(x)>f(a), значение на концах функции равны Пусть f(x)>f(a), по условию f(a)=f(b)=>f(x)>f(b) f’(c)=0
|
|||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 607; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.116.47.4 (0.01 с.) |

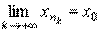
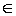 [ a, b ]. Вследствие непрерывности функции в точке х 0 должно быть выполнено
[ a, b ]. Вследствие непрерывности функции в точке х 0 должно быть выполнено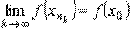
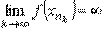
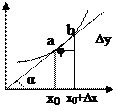 Производной функции у=ƒ(х) β точке х0 называется предел отношения приращения функции к приращению аргумента, когда приращение аргумента стремится к нулю.
Производной функции у=ƒ(х) β точке х0 называется предел отношения приращения функции к приращению аргумента, когда приращение аргумента стремится к нулю.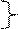
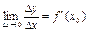
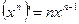
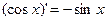
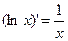
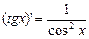
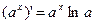
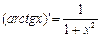

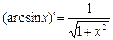
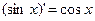
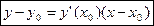 .
.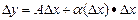 .
.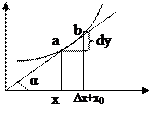
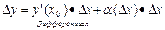
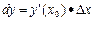
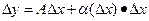
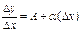
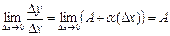 , т.е. выражение
, т.е. выражение 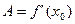
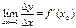
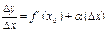
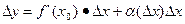
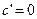

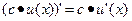
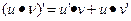
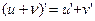
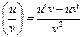
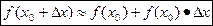
 Найдет такая точка С, в которой касательная будет горизонтальна в этой точке производная равна 0.
Найдет такая точка С, в которой касательная будет горизонтальна в этой точке производная равна 0. Доказательство: Пусть функция f(x) – постоянна х ∈ (a;b), тогда значение производной во всех точках равно 0.
Доказательство: Пусть функция f(x) – постоянна х ∈ (a;b), тогда значение производной во всех точках равно 0.



