

Мы поможем в написании ваших работ!
ЗНАЕТЕ ЛИ ВЫ?
|
Экстремумы функций двух переменных
Похожие статьи вашей тематики
По аналогии с понятием экстремума для функций одного переменного введем следующее определение. Пусть точка  входит в область определения функции входит в область определения функции  с некоторой ее окрестностью (т.е. со всеми точками некоторого круга с центром в этой точке). Точка с некоторой ее окрестностью (т.е. со всеми точками некоторого круга с центром в этой точке). Точка  называется точкой максимума (минимума) функции называется точкой максимума (минимума) функции  , если значение функции в этой точке больше или равно (меньше или равно) значений функции во всех ближайших к , если значение функции в этой точке больше или равно (меньше или равно) значений функции во всех ближайших к  точках, т.е. точках, т.е.  ( (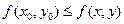 ) для всех точек ) для всех точек  из какой-либо окрестности точки из какой-либо окрестности точки  . Точки максимума и минимума функции называются точками экстремума этой функции. В практических задачах принятие оптимального решения сводится обычно к поиску экстремумов некоторой функции. Как же ищутся точки экстремуму для функции двух переменных? Если вспомнить, то точки экстремума функции одного переменного находились среди ее критических точек (т.е. точек, в которых производная не существовала или обращалась в 0). По аналогии, назовем критическими точками функции двух переменных . Точки максимума и минимума функции называются точками экстремума этой функции. В практических задачах принятие оптимального решения сводится обычно к поиску экстремумов некоторой функции. Как же ищутся точки экстремуму для функции двух переменных? Если вспомнить, то точки экстремума функции одного переменного находились среди ее критических точек (т.е. точек, в которых производная не существовала или обращалась в 0). По аналогии, назовем критическими точками функции двух переменных  такие точки (на координатной плоскости такие точки (на координатной плоскости 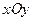 ), в которых либо не существует хотя бы одна из ее частных производных, либо обе они, существуя, обращаются в 0. Точки, в которых обе частные производные существуют и одновременно обращаются в 0, называются стационарными точками функции. Таким образом, критические точки функции состоят из ее стационарных точек и точек, в которых не существует хотя бы одна из ее частных производных. Важную роль таких точек обеспечивает ), в которых либо не существует хотя бы одна из ее частных производных, либо обе они, существуя, обращаются в 0. Точки, в которых обе частные производные существуют и одновременно обращаются в 0, называются стационарными точками функции. Таким образом, критические точки функции состоят из ее стационарных точек и точек, в которых не существует хотя бы одна из ее частных производных. Важную роль таких точек обеспечивает
Теорема 1(необходимое условие экстремума). Пусть в точке  функция функция  имеет экстремум и в ней существуют обе частные производные. Тогда они необходимо обращаются в 0: имеет экстремум и в ней существуют обе частные производные. Тогда они необходимо обращаются в 0:  , ,  . .
Эта теорема позволяет сделать тот же вывод, что был сделан для функции одного переменного: все экстремумы функции  находятся только среди ее критических точек. Однако точно так же, как и в случае функции одного переменного, не всякая критическая точка функции двух переменных обязательно является точкой ее экстремума. Например, для функции находятся только среди ее критических точек. Однако точно так же, как и в случае функции одного переменного, не всякая критическая точка функции двух переменных обязательно является точкой ее экстремума. Например, для функции  начало координат начало координат  является критической точкой, так как в ней обращаются в 0 обе частные производные: является критической точкой, так как в ней обращаются в 0 обе частные производные: 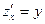 , , 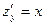 . Однако эта точка не является ни точкой максимума, ни точкой минимума, поскольку значение функции в начале координат, очевидно, равно 0, а в любой сколь угодно малой окрестности начала координат (т.е. в любом круге с центром в начале координат) есть точки, в которых функция принимает как отрицательные (в точках II и IV четверти), так и положительные (I и III четверть) значения (т.е. как меньшие значения, чем в точке . Однако эта точка не является ни точкой максимума, ни точкой минимума, поскольку значение функции в начале координат, очевидно, равно 0, а в любой сколь угодно малой окрестности начала координат (т.е. в любом круге с центром в начале координат) есть точки, в которых функция принимает как отрицательные (в точках II и IV четверти), так и положительные (I и III четверть) значения (т.е. как меньшие значения, чем в точке  , так и большие). , так и большие).
Поэтому снова (как и в случае функций одного переменного) необходим алгоритм, позволяющий определить, является ли данная критическая точка точкой экстремума или нет. А если является, то максимумом или минимумом? Такой алгоритм дает
Теорема 2 (достаточное условие экстремума). Пусть  – стационарная точка функции – стационарная точка функции  , в некоторой окрестности которой существуют и непрерывны все частные производные второго порядка. Пусть , в некоторой окрестности которой существуют и непрерывны все частные производные второго порядка. Пусть  , ,  , ,  , а , а  . .
Тогда
а) Если  , то в точке , то в точке  экстремум есть (при экстремум есть (при 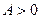 минимум, при минимум, при  максимум). максимум).
б) Если  , то в точке , то в точке  экстремума нет. экстремума нет.
Приведенные выше рассуждения позволяют предложить следующую схему нахождения экстремумов функции двух переменных  : :
· Находим выражения для частных производных  и и  . .
· Находим критические точки функции; это либо стационарные точки, в которых обе частные производные обращаются в 0 (координаты таких точек есть решения системы  ), либо точки, в которых не существует хотя бы одна из найденных частных производных (в этих точках не определено хотя бы одно из выражений для найденных частных производных ), либо точки, в которых не существует хотя бы одна из найденных частных производных (в этих точках не определено хотя бы одно из выражений для найденных частных производных  и и  ). ).
· Находим выражения для вторых производных  , ,  и и  . .
Дальнейшие пункты схемы делаются отдельно для каждой из найденных стационарных точек, входящих в состав найденных критических точек. Пусть исследуется стационарная точка  . .
· Подставляя координаты 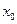 и и  исследуемой точки в выражения для вторых производных, находим числа исследуемой точки в выражения для вторых производных, находим числа  , ,  , ,  . .
· Находим значение  . .
· Делаем вывод о характере исследуемой точки  в соответствии с заключением приведенной теоремы: если в соответствии с заключением приведенной теоремы: если  , то в точке , то в точке  экстремум есть (при экстремум есть (при 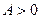 минимум, при минимум, при  максимум), а если максимум), а если  , то в точке , то в точке  экстремума нет. экстремума нет.
· Если  оказалась точкой экстремума, то находим соответствующее экстремальное значение функции оказалась точкой экстремума, то находим соответствующее экстремальное значение функции  , подставляя в выражение для функции , подставляя в выражение для функции  координаты координаты 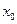 и и  этой точки. этой точки.
Большим недостатком теоремы является то, что она не отвечает на вопрос о характере стационарной точки в случае, когда  . В этом случае характер этой точки выявляется дополнительным исследованием. Такое исследование требуется и в том случае, когда исследуется критическая точка, не являющаяся стационарной (т.е. к ней не применима теорема 2). Приведем иллюстрирующий эту ситуацию . В этом случае характер этой точки выявляется дополнительным исследованием. Такое исследование требуется и в том случае, когда исследуется критическая точка, не являющаяся стационарной (т.е. к ней не применима теорема 2). Приведем иллюстрирующий эту ситуацию
Пример 1. Найти точки экстремума функции  . .
Решение. В соответствии с приведенной схемой находим выражения для частных производных:  , аналогично , аналогично 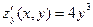 . Оба получившихся выражения для производных . Оба получившихся выражения для производных  и и 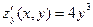 можно, очевидно, вычислить при любых значениях можно, очевидно, вычислить при любых значениях  и и  , а потому частные производные существуют для всех точек координатной плоскости , а потому частные производные существуют для всех точек координатной плоскости  . Тогда критическими могут быть только стационарные точки, т.е. точки, в которых обе производные обращаются в 0. Для нахождения координат таких точек решаем систему . Тогда критическими могут быть только стационарные точки, т.е. точки, в которых обе производные обращаются в 0. Для нахождения координат таких точек решаем систему  , т.е. , т.е. 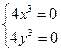 . Решением такой системы является, очевидно, единственная пара чисел: . Решением такой системы является, очевидно, единственная пара чисел: 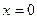 , ,  . Поэтому единственной критической точкой является начало координат . Поэтому единственной критической точкой является начало координат  . В соответствии с дальнейшими пунктами схемы находим вторые производные: . В соответствии с дальнейшими пунктами схемы находим вторые производные: 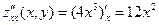 , ,  и и 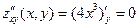 . Подставляя координаты . Подставляя координаты 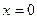 и и  критической точки критической точки  в выражения для вторых производных, получим: в выражения для вторых производных, получим:  , ,  . Отметим, что выражение для . Отметим, что выражение для  (а мы получили, что (а мы получили, что  ) не содержит ) не содержит  и и  , а просто равно числу 0. Это говорит о том, что эта производная является постоянной, т.е. принимает одно и то же значение (равное 0) в любой точке. Поэтому такое же значения она принимает и в критической точке , а просто равно числу 0. Это говорит о том, что эта производная является постоянной, т.е. принимает одно и то же значение (равное 0) в любой точке. Поэтому такое же значения она принимает и в критической точке  , а потому , а потому 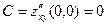 . Тогда число . Тогда число  . Таким образом, в данном примере как раз возник тот случай, в котором приведенная схема не отвечает на вопрос о наличии или отсутствии экстремума в критической точке . Таким образом, в данном примере как раз возник тот случай, в котором приведенная схема не отвечает на вопрос о наличии или отсутствии экстремума в критической точке  , а потому для ответа на этот вопрос требуются (как сказано выше) дополнительные исследования. Проведем их. Значение исследуемой функции , а потому для ответа на этот вопрос требуются (как сказано выше) дополнительные исследования. Проведем их. Значение исследуемой функции  в точке в точке  равно равно  . С другой стороны, значение этой функции в любой другой точке строго больше 0: . С другой стороны, значение этой функции в любой другой точке строго больше 0: 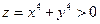 , если хотя бы одно из чисел , если хотя бы одно из чисел  или или  отлично от 0 (это следует из того, что четвертая степень любого отличного от 0 числа строго положительна). Таким образом, значение функции в точке отлично от 0 (это следует из того, что четвертая степень любого отличного от 0 числа строго положительна). Таким образом, значение функции в точке  меньше значения функции в любой другой точке. Тогда по определению точка меньше значения функции в любой другой точке. Тогда по определению точка  является точкой минимума данной функции, а соответствующее минимальное значение является точкой минимума данной функции, а соответствующее минимальное значение  . .
Следующий пример также демонстрирует бессилие приведенной схемы в случае, если  , однако, дополнительные исследования приводят уже к другому выводу. , однако, дополнительные исследования приводят уже к другому выводу.
Пример 2. Найти точки экстремума функции 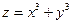 . .
Решение. Функция очень похожа на функцию в предыдущем примере, поэтому все выкладки можно делать короче. Имеем  , ,  . Для нахождения координат критических точек решаем систему . Для нахождения координат критических точек решаем систему  , т.е. , т.е.  . Решением такой системы снова является единственная пара чисел: . Решением такой системы снова является единственная пара чисел: 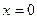 , ,  . Поэтому опять единственной критической точкой является начало координат . Поэтому опять единственной критической точкой является начало координат  . Далее, . Далее,  , ,  , , 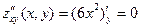 . Тогда . Тогда  , ,  , , 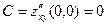 , а потому опять , а потому опять  . Снова возник тот случай, в котором приведенная схема не отвечает на вопрос о наличии или отсутствии экстремума в критической точке . Снова возник тот случай, в котором приведенная схема не отвечает на вопрос о наличии или отсутствии экстремума в критической точке  , а потому для ответа на этот вопрос опять требуются дополнительные исследования. Проведем их. Значение исследуемой функции , а потому для ответа на этот вопрос опять требуются дополнительные исследования. Проведем их. Значение исследуемой функции 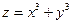 в точке в точке  равно равно  . С другой стороны, какую бы маленькую окрестность точки . С другой стороны, какую бы маленькую окрестность точки  (т.е. кружок с центром в начале координат) мы ни взяли, в ней всегда найдутся точки из I и III четверти. Но в точках первой четверти (обе координаты таких точек положительны) значение исследуемой функции (т.е. кружок с центром в начале координат) мы ни взяли, в ней всегда найдутся точки из I и III четверти. Но в точках первой четверти (обе координаты таких точек положительны) значение исследуемой функции 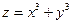 строго больше 0 (сумма кубов двух положительных чисел положительна), а в точках третей четверти (обе координаты таких точек отрицательны) значение этой функции строго больше 0 (сумма кубов двух положительных чисел положительна), а в точках третей четверти (обе координаты таких точек отрицательны) значение этой функции 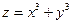 строго меньше 0 (сумма кубов двух отрицательных чисел отрицательна). Таким образом, в любой окрестности точки строго меньше 0 (сумма кубов двух отрицательных чисел отрицательна). Таким образом, в любой окрестности точки  всегда есть точки, значения в которых как больше значения функции в этой точке, так и меньше. Поэтому по определению точка всегда есть точки, значения в которых как больше значения функции в этой точке, так и меньше. Поэтому по определению точка  не может быть точкой экстремума. А так как на подозрении в наличии экстремума у нас была только эта точка (напомним – все экстремумы только среди критических точек!), то можно сделать вывод, что у данной функции вообще экстремумов нет. не может быть точкой экстремума. А так как на подозрении в наличии экстремума у нас была только эта точка (напомним – все экстремумы только среди критических точек!), то можно сделать вывод, что у данной функции вообще экстремумов нет.
Далее рассмотрим примеры, где указанная схема работает до конца.
Пример 3. Найти точки экстремума функции  . .
Решение. В соответствии с приведенной схемой находим выражения для частных производных:   , аналогично , аналогично  . Оба получившихся выражения для производных определены при любых значениях . Оба получившихся выражения для производных определены при любых значениях  и и  , а потому частные производные существуют для всех точек координатной плоскости , а потому частные производные существуют для всех точек координатной плоскости 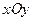 . Поэтому критическими могут быть только стационарные точки, т.е. точки, в которых обе производные обращаются в 0. Для нахождения координат таких точек решаем систему . Поэтому критическими могут быть только стационарные точки, т.е. точки, в которых обе производные обращаются в 0. Для нахождения координат таких точек решаем систему  , т.е. , т.е. 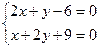 . Выражаем из первого уравнения . Выражаем из первого уравнения  и подставляем во второе: и подставляем во второе:  , откуда получаем , откуда получаем 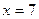 . Поэтому . Поэтому  . Итак, единственным решением системы является пара чисел: . Итак, единственным решением системы является пара чисел: 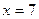 , , 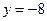 , а потому единственной критической точкой является точка , а потому единственной критической точкой является точка  . В соответствии с дальнейшими пунктами схемы, находим вторые производные: . В соответствии с дальнейшими пунктами схемы, находим вторые производные:  , ,   . Выражения для вторых производных не содержат . Выражения для вторых производных не содержат  и и  , а просто равны некоторым числам. Поэтому каждая вторая производная является постоянной, т.е. принимает одно и то же значение в любой точке. Поэтому такие же значения они принимают и в исследуемой критической точке , а просто равны некоторым числам. Поэтому каждая вторая производная является постоянной, т.е. принимает одно и то же значение в любой точке. Поэтому такие же значения они принимают и в исследуемой критической точке  : :  , ,   . Тогда число . Тогда число  . Поскольку число . Поскольку число 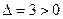 , то (в соответствии с описанной схемой) исследуемая критическая точка , то (в соответствии с описанной схемой) исследуемая критическая точка  действительно является точкой экстремума. Поскольку выше получилось действительно является точкой экстремума. Поскольку выше получилось  , то это точка минимума. Минимальное значение функции – ее значение в этой точке, поэтому , то это точка минимума. Минимальное значение функции – ее значение в этой точке, поэтому  . Итак, функция . Итак, функция  имеет одну точку минимума имеет одну точку минимума  , причем , причем 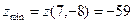 . .
Пример 4. Найти точки экстремума функции  . .
Решение. Находим частные производные:  , , 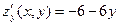 . Обе производные определены при любых значениях . Обе производные определены при любых значениях  и и  , а потому критическими могут быть только стационарные точки. Для нахождения координат таких точек решаем систему , а потому критическими могут быть только стационарные точки. Для нахождения координат таких точек решаем систему  , т.е. , т.е.  . Получившаяся система решается очень просто (в отличии от системы в предыдущем примере, которая решалась просто «просто»), поскольку в первом уравнении есть только иксы, а во втором только игреки, а потому из каждого уравнения можно сразу найти соответствующее неизвестное: . Получившаяся система решается очень просто (в отличии от системы в предыдущем примере, которая решалась просто «просто»), поскольку в первом уравнении есть только иксы, а во втором только игреки, а потому из каждого уравнения можно сразу найти соответствующее неизвестное: 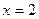 , ,  . Итак, единственной критической точкой является точка . Итак, единственной критической точкой является точка  . В соответствии с дальнейшими пунктами схемы, далее находим вторые производные: . В соответствии с дальнейшими пунктами схемы, далее находим вторые производные: 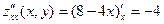 , ,   , а потому , а потому  , , 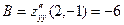  . Тогда число . Тогда число  , поэтому критическая точка , поэтому критическая точка  является точкой экстремума. Поскольку выше получилось является точкой экстремума. Поскольку выше получилось  , то это точка максимума. Максимальное значение функции – ее значение в этой точке, поэтому , то это точка максимума. Максимальное значение функции – ее значение в этой точке, поэтому  . Итак, исследуемая функция . Итак, исследуемая функция  имеет одну точку максимума имеет одну точку максимума  , причем , причем 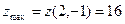 . .
Пример 5. Найти точки экстремума функции  . .
Решение. Частные производные первого порядка:  , аналогично , аналогично  . Критическими снова могут быть только стационарные точки. Для нахождения координат таких точек решаем систему . Критическими снова могут быть только стационарные точки. Для нахождения координат таких точек решаем систему  , т.е. , т.е.  . Деля обе части первого уравнения на 2, второго – на 4 и перенося числа в правую часть, получим следующую систему для определения координат стационарных точек: . Деля обе части первого уравнения на 2, второго – на 4 и перенося числа в правую часть, получим следующую систему для определения координат стационарных точек:  . Оказывается, что эта система несовместна, т.е. не имеет ни одного решения. Это можно доказать с помощью теоремы Кронекера- Капели (эта теорема была в разделе «Основы линейной алгебры»), убедившись, что ранги основной и расширенной матриц системы не совпадают. Если эти методы уже забылись, то можно действовать и «школьными» приемами. Для этого выразим из первого уравнения . Оказывается, что эта система несовместна, т.е. не имеет ни одного решения. Это можно доказать с помощью теоремы Кронекера- Капели (эта теорема была в разделе «Основы линейной алгебры»), убедившись, что ранги основной и расширенной матриц системы не совпадают. Если эти методы уже забылись, то можно действовать и «школьными» приемами. Для этого выразим из первого уравнения  и подставим во второе: и подставим во второе:  , ,  , , 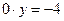 . Последнее уравнение, очевидно, решений не имеет, так как не существует такого числа, которое, будучи умноженным на 0, даст . Последнее уравнение, очевидно, решений не имеет, так как не существует такого числа, которое, будучи умноженным на 0, даст 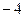 . Поэтому и вся система решений не имеет. Что же это означает? Решения этой системы давали нам координаты критических точек. Отсутствие решений системы говорит об отсутствии критических точек у исследуемой функции. Но поскольку все экстремумы функции находятся только среди ее критических точек, то у данной функции экстремумов нет. . Поэтому и вся система решений не имеет. Что же это означает? Решения этой системы давали нам координаты критических точек. Отсутствие решений системы говорит об отсутствии критических точек у исследуемой функции. Но поскольку все экстремумы функции находятся только среди ее критических точек, то у данной функции экстремумов нет.
Пример 6. Найти точки экстремума функции 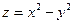 . .
Решение. Находим частные производные:  , ,  . Ищем координаты критических точек: . Ищем координаты критических точек:  , т.е. , т.е.  . Ясно, что система имеет единственное решение . Ясно, что система имеет единственное решение 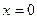 , ,  . Поэтому единственной критической точкой является начало координат . Поэтому единственной критической точкой является начало координат  . Далее, . Далее,  , ,  , ,  . Тогда . Тогда  , ,  , , 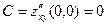 , а потому , а потому  . Итак, . Итак, 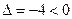 , потому по приведенной выше теореме экстремумов в точке , потому по приведенной выше теореме экстремумов в точке  нет. Но эта точка была единственной точкой, в которой мог быть экстремум (все экстремумы – только среди критических точек функции!). Поэтому у данной функции экстремумов нет. нет. Но эта точка была единственной точкой, в которой мог быть экстремум (все экстремумы – только среди критических точек функции!). Поэтому у данной функции экстремумов нет.
Пример 7. Найти точки экстремума функции  . .
Решение. Выражения для частных производных:  , ,  . Оба получившихся выражения для производных определены при любых значениях . Оба получившихся выражения для производных определены при любых значениях  и и  , а потому частные производные существуют для всех точек координатной плоскости , а потому частные производные существуют для всех точек координатной плоскости 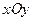 . Поэтому критическими могут быть только стационарные точки, для нахождения координат которых решаем систему . Поэтому критическими могут быть только стационарные точки, для нахождения координат которых решаем систему  , т.е. , т.е.  . Сокращая уравнения на 3, получим . Сокращая уравнения на 3, получим  . Выражаем из первого уравнения . Выражаем из первого уравнения 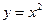 и подставляем во второе: и подставляем во второе:  , ,  , ,  . Произведение может обратиться в 0 только при тех значениях . Произведение может обратиться в 0 только при тех значениях  , которые обращают в 0 хотя бы один из сомножителей. Поэтому либо , которые обращают в 0 хотя бы один из сомножителей. Поэтому либо 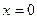 , либо , либо  , т.е. , т.е.  . Таким образом, уравнение имеет два корня: . Таким образом, уравнение имеет два корня: 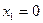 и и  . Учитывая полученную ранее связь . Учитывая полученную ранее связь 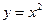 , получим соответствующие значения , получим соответствующие значения  : :  , ,  . Потому система имеет 2 решения: . Потому система имеет 2 решения:  , ,  и и  , ,  , а исследуемая функция имеет, соответственно, две критические точки: , а исследуемая функция имеет, соответственно, две критические точки:  и и  . В соответствии с дальнейшими пунктами схемы, находим выражения для вторых производных: . В соответствии с дальнейшими пунктами схемы, находим выражения для вторых производных:  , ,   . .
Далее, в соответствии с приведенной схемой исследуем обе критические точки  и и  по отдельности. по отдельности.
1. Исследуем критическую точку  . Вычисляем в этой точке значения вторых производных: . Вычисляем в этой точке значения вторых производных:  , ,   . Тогда число . Тогда число  . Поскольку число . Поскольку число  , то (в соответствии с описанной схемой) исследуемая критическая точка , то (в соответствии с описанной схемой) исследуемая критическая точка  не является точкой экстремума. не является точкой экстремума.
2. Исследуем критическую точку  . Вычисляем в этой точке значения вторых производных: . Вычисляем в этой точке значения вторых производных: 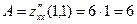 , ,   . Тогда число . Тогда число  . Поскольку число . Поскольку число 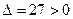 , то (в соответствии с описанной схемой) исследуемая критическая точка , то (в соответствии с описанной схемой) исследуемая критическая точка  является точкой экстремума. Поскольку является точкой экстремума. Поскольку  , то , то  − точка минимума. Значение функции в точке минимума: − точка минимума. Значение функции в точке минимума:  . .
Итак, функция  имеет единственную точку минимума имеет единственную точку минимума  , причем , причем  . .
Пример 8. Найти точки экстремума функции  . .
Решение. Выражения для частных производных:  ={производная произведения: ={производная произведения:  }= }=   , аналогично , аналогично  {первый множитель не содержит {первый множитель не содержит  , а потому при вычислении производной по этой переменной считается постоянным множителем и выносится за знак производной}= , а потому при вычислении производной по этой переменной считается постоянным множителем и выносится за знак производной}=  . Оба получившихся выражения для производных определены при любых значениях . Оба получившихся выражения для производных определены при любых значениях  и и  , а потому частные производные существуют для всех точек координатной плоскости , а потому частные производные существуют для всех точек координатной плоскости 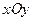 . Поэтому критическими могут быть только стационарные точки, для нахождения координат которых решаем систему . Поэтому критическими могут быть только стационарные точки, для нахождения координат которых решаем систему  , т.е. , т.е.  . Поскольку . Поскольку  не обращается в 0 ни при каких значениях показателя степени не обращается в 0 ни при каких значениях показателя степени  , то, разделив обе части первого уравнения на , то, разделив обе части первого уравнения на  , а второго на , а второго на  , получим систему, равносильную исходной: , получим систему, равносильную исходной:  . Подставляя . Подставляя  в первое уравнение, получим в первое уравнение, получим  . Итак, единственным решением системы является пара чисел: . Итак, единственным решением системы является пара чисел:  , ,  , а потому единственной критической точкой является точка , а потому единственной критической точкой является точка  . Далее, находим вторые производные: . Далее, находим вторые производные:    , ,  , , 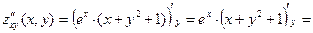  . Вычисляем значения вторых производных в исследуемой критической точке . Вычисляем значения вторых производных в исследуемой критической точке  : :  , , 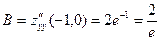 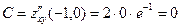 . Тогда число . Тогда число  . Поэтому исследуемая критическая точка . Поэтому исследуемая критическая точка  действительно является точкой экстремума. Поскольку действительно является точкой экстремума. Поскольку  , то это точка минимума. Минимальное значение функции , то это точка минимума. Минимальное значение функции  . Итак, функция . Итак, функция  имеет одну точку минимума имеет одну точку минимума  , причем , причем  . .
 Пример 9. Необходимо построить открытый бассейн в форме прямого параллелепипеда объемом Пример 9. Необходимо построить открытый бассейн в форме прямого параллелепипеда объемом 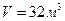 , на облицовку дна и стен которого пойдет наименьшее количество материала. , на облицовку дна и стен которого пойдет наименьшее количество материала.
Решение. Обозначим размеры бассейна (длину, ширину и глубину в метрах) через  , ,  и и  (см. рисунок). Понятно, что чем меньше необходимая площадь облицовки, тем меньше будет использовано облицовочного материала. Таким образом, встает следующая задача. Подобрать такие числа (см. рисунок). Понятно, что чем меньше необходимая площадь облицовки, тем меньше будет использовано облицовочного материала. Таким образом, встает следующая задача. Подобрать такие числа  , ,  и и  − размеры параллелепипеда (бассейна), чтобы его объем − размеры параллелепипеда (бассейна), чтобы его объем  был равен был равен  , а суммарная площадь основания и боковой поверхности (это как раз дно и стены бассейна) была бы наименьшей. Выразим эту площадь через размеры параллелепипеда. Указанная площадь (обозначим ее , а суммарная площадь основания и боковой поверхности (это как раз дно и стены бассейна) была бы наименьшей. Выразим эту площадь через размеры параллелепипеда. Указанная площадь (обозначим ее  ) складывается из площади прямоугольника-основания (равной ) складывается из площади прямоугольника-основания (равной  ), площадей передней и задней стенок (равных ), площадей передней и задней стенок (равных  каждая) и площадей левой и правой стенок (по каждая) и площадей левой и правой стенок (по  каждая). Таким образом, площадь облицовки каждая). Таким образом, площадь облицовки  следующим образом зависит трех переменных – размеров бассейна следующим образом зависит трех переменных – размеров бассейна  , ,  и и  : :  или или  . Требуется найти точку минимума этой функции. Поскольку мы изучили методы отыскания экстремумов функции двух (а не трех) переменных, то от одной переменной надо избавиться. Это можно сделать, если понять, что размеры бассейна . Требуется найти точку минимума этой функции. Поскольку мы изучили методы отыскания экстремумов функции двух (а не трех) переменных, то от одной переменной надо избавиться. Это можно сделать, если понять, что размеры бассейна  , ,  и и  не могут быть выбраны независимо друг от друга. Если выбраны его длина не могут быть выбраны независимо друг от друга. Если выбраны его длина  и ширина и ширина  , то глубина , то глубина  не может быть выбрана произвольно, так как выбираемая при этом глубина должна быть такой, чтобы обеспечить требование о необходимом объеме получающегося бассейна: не может быть выбрана произвольно, так как выбираемая при этом глубина должна быть такой, чтобы обеспечить требование о необходимом объеме получающегося бассейна: 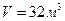 . Поскольку объем параллелепипеда равен произведению всех его измерений, то должно выполняться требование: . Поскольку объем параллелепипеда равен произведению всех его измерений, то должно выполняться требование:  , откуда , откуда 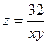 . Поэтому если выбраны длина . Поэтому если выбраны длина  и ширина и ширина  бассейна, то глубина бассейна, то глубина  однозначно определена: однозначно определена:  . Подставляя это выражение в полученную выше формулу . Подставляя это выражение в полученную выше формулу  для площади, получаем площадь как функцию двух переменных для площади, получаем площадь как функцию двух переменных  и и  : :  . Раскрывая скобки, получим более удобное для исследования выражение: . Раскрывая скобки, получим более удобное для исследования выражение:  или или  . По смыслу задачи ( . По смыслу задачи ( и и  − размеры бассейна) эту функцию мы рассматриваем только при положительных значениях переменных − размеры бассейна) эту функцию мы рассматриваем только при положительных значениях переменных  и и  : :  , ,  . Поэтому областью определения этой функции является I четверть без точек, лежащих на осях координат. Найдем экстремумы этой функции двух переменных по привычной схеме. Находим первые производные: . Поэтому областью определения этой функции является I четверть без точек, лежащих на осях координат. Найдем экстремумы этой функции двух переменных по привычной схеме. Находим первые производные: 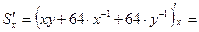  . Таким образом, . Таким образом,  или или  . Аналогично можно получить выражение для другой частной производной: . Аналогично можно получить выражение для другой частной производной:  или или  . Находим критические точки. Производная . Находим критические точки. Производная  не существует для всех точек, у которых первая координата не существует для всех точек, у которых первая координата 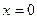 , т.е. для всех точек, лежащих на оси , т.е. для всех точек, лежащих на оси  . Аналогично, производная . Аналогично, производная  не существует для всех точек, у которых вторая координата не существует для всех точек, у которых вторая координата  , т.е. для всех точек, лежащих на оси , т.е. для всех точек, лежащих на оси  . Однако все эти точки не входят в область определения исследуемой функции, а потому не являются критическими точками функции и не интересуют нас как потенциальные точки экстремума. Найдем теперь те критические точки функции, которые являются ее стационарными точками. Для нахождения координат этих точек решаем систему . Однако все эти точки не входят в область определения исследуемой функции, а потому не являются критическими точками функции и не интересуют нас как потенциальные точки экстремума. Найдем теперь те критические точки функции, которые являются ее стационарными точками. Для нахождения координат этих точек решаем систему  , т.е. , т.е.  . Из первого уравнения выразим . Из первого уравнения выразим 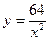 и подставим во второе уравнение: и подставим во второе уравнение:  , , 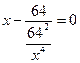 , ,  |



 входит в область определения функции
входит в область определения функции  с некоторой ее окрестностью (т.е. со всеми точками некоторого круга с центром в этой точке). Точка
с некоторой ее окрестностью (т.е. со всеми точками некоторого круга с центром в этой точке). Точка  (
(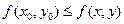 ) для всех точек
) для всех точек  из какой-либо окрестности точки
из какой-либо окрестности точки 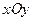 ), в которых либо не существует хотя бы одна из ее частных производных, либо обе они, существуя, обращаются в 0. Точки, в которых обе частные производные существуют и одновременно обращаются в 0, называются стационарными точками функции. Таким образом, критические точки функции состоят из ее стационарных точек и точек, в которых не существует хотя бы одна из ее частных производных. Важную роль таких точек обеспечивает
), в которых либо не существует хотя бы одна из ее частных производных, либо обе они, существуя, обращаются в 0. Точки, в которых обе частные производные существуют и одновременно обращаются в 0, называются стационарными точками функции. Таким образом, критические точки функции состоят из ее стационарных точек и точек, в которых не существует хотя бы одна из ее частных производных. Важную роль таких точек обеспечивает ,
,  .
. начало координат
начало координат  является критической точкой, так как в ней обращаются в 0 обе частные производные:
является критической точкой, так как в ней обращаются в 0 обе частные производные: 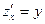 ,
, 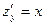 . Однако эта точка не является ни точкой максимума, ни точкой минимума, поскольку значение функции в начале координат, очевидно, равно 0, а в любой сколь угодно малой окрестности начала координат (т.е. в любом круге с центром в начале координат) есть точки, в которых функция принимает как отрицательные (в точках II и IV четверти), так и положительные (I и III четверть) значения (т.е. как меньшие значения, чем в точке
. Однако эта точка не является ни точкой максимума, ни точкой минимума, поскольку значение функции в начале координат, очевидно, равно 0, а в любой сколь угодно малой окрестности начала координат (т.е. в любом круге с центром в начале координат) есть точки, в которых функция принимает как отрицательные (в точках II и IV четверти), так и положительные (I и III четверть) значения (т.е. как меньшие значения, чем в точке  ,
,  ,
,  , а
, а  .
. , то в точке
, то в точке 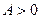 минимум, при
минимум, при  максимум).
максимум). , то в точке
, то в точке  и
и  .
. ), либо точки, в которых не существует хотя бы одна из найденных частных производных (в этих точках не определено хотя бы одно из выражений для найденных частных производных
), либо точки, в которых не существует хотя бы одна из найденных частных производных (в этих точках не определено хотя бы одно из выражений для найденных частных производных  ,
,  и
и  .
.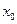 и
и  исследуемой точки в выражения для вторых производных, находим числа
исследуемой точки в выражения для вторых производных, находим числа  , подставляя в выражение для функции
, подставляя в выражение для функции  . В этом случае характер этой точки выявляется дополнительным исследованием. Такое исследование требуется и в том случае, когда исследуется критическая точка, не являющаяся стационарной (т.е. к ней не применима теорема 2). Приведем иллюстрирующий эту ситуацию
. В этом случае характер этой точки выявляется дополнительным исследованием. Такое исследование требуется и в том случае, когда исследуется критическая точка, не являющаяся стационарной (т.е. к ней не применима теорема 2). Приведем иллюстрирующий эту ситуацию .
. , аналогично
, аналогично 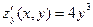 . Оба получившихся выражения для производных
. Оба получившихся выражения для производных  и
и  и
и  , а потому частные производные существуют для всех точек координатной плоскости
, а потому частные производные существуют для всех точек координатной плоскости 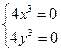 . Решением такой системы является, очевидно, единственная пара чисел:
. Решением такой системы является, очевидно, единственная пара чисел: 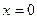 ,
,  . Поэтому единственной критической точкой является начало координат
. Поэтому единственной критической точкой является начало координат 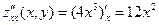 ,
,  и
и 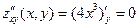 . Подставляя координаты
. Подставляя координаты  ,
,  . Отметим, что выражение для
. Отметим, что выражение для  ) не содержит
) не содержит 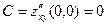 . Тогда число
. Тогда число  . Таким образом, в данном примере как раз возник тот случай, в котором приведенная схема не отвечает на вопрос о наличии или отсутствии экстремума в критической точке
. Таким образом, в данном примере как раз возник тот случай, в котором приведенная схема не отвечает на вопрос о наличии или отсутствии экстремума в критической точке  . С другой стороны, значение этой функции в любой другой точке строго больше 0:
. С другой стороны, значение этой функции в любой другой точке строго больше 0: 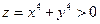 , если хотя бы одно из чисел
, если хотя бы одно из чисел  .
. , однако, дополнительные исследования приводят уже к другому выводу.
, однако, дополнительные исследования приводят уже к другому выводу.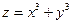 .
. ,
,  . Для нахождения координат критических точек решаем систему
. Для нахождения координат критических точек решаем систему  . Решением такой системы снова является единственная пара чисел:
. Решением такой системы снова является единственная пара чисел:  ,
,  ,
, 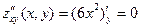 . Тогда
. Тогда  ,
,  ,
,  . С другой стороны, какую бы маленькую окрестность точки
. С другой стороны, какую бы маленькую окрестность точки  .
.
 , аналогично
, аналогично  . Оба получившихся выражения для производных определены при любых значениях
. Оба получившихся выражения для производных определены при любых значениях 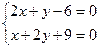 . Выражаем из первого уравнения
. Выражаем из первого уравнения  и подставляем во второе:
и подставляем во второе:  , откуда получаем
, откуда получаем 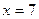 . Поэтому
. Поэтому  . Итак, единственным решением системы является пара чисел:
. Итак, единственным решением системы является пара чисел: 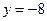 , а потому единственной критической точкой является точка
, а потому единственной критической точкой является точка  . В соответствии с дальнейшими пунктами схемы, находим вторые производные:
. В соответствии с дальнейшими пунктами схемы, находим вторые производные:  ,
, 
 . Выражения для вторых производных не содержат
. Выражения для вторых производных не содержат  ,
, 
 . Тогда число
. Тогда число  . Поскольку число
. Поскольку число 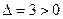 , то (в соответствии с описанной схемой) исследуемая критическая точка
, то (в соответствии с описанной схемой) исследуемая критическая точка  , то это точка минимума. Минимальное значение функции – ее значение в этой точке, поэтому
, то это точка минимума. Минимальное значение функции – ее значение в этой точке, поэтому  . Итак, функция
. Итак, функция 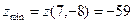 .
. .
. ,
, 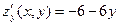 . Обе производные определены при любых значениях
. Обе производные определены при любых значениях  . Получившаяся система решается очень просто (в отличии от системы в предыдущем примере, которая решалась просто «просто»), поскольку в первом уравнении есть только иксы, а во втором только игреки, а потому из каждого уравнения можно сразу найти соответствующее неизвестное:
. Получившаяся система решается очень просто (в отличии от системы в предыдущем примере, которая решалась просто «просто»), поскольку в первом уравнении есть только иксы, а во втором только игреки, а потому из каждого уравнения можно сразу найти соответствующее неизвестное: 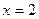 ,
,  . Итак, единственной критической точкой является точка
. Итак, единственной критической точкой является точка  . В соответствии с дальнейшими пунктами схемы, далее находим вторые производные:
. В соответствии с дальнейшими пунктами схемы, далее находим вторые производные: 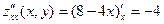 ,
, 
 , а потому
, а потому  ,
, 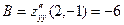
 . Тогда число
. Тогда число  , поэтому критическая точка
, поэтому критическая точка  , то это точка максимума. Максимальное значение функции – ее значение в этой точке, поэтому
, то это точка максимума. Максимальное значение функции – ее значение в этой точке, поэтому  . Итак, исследуемая функция
. Итак, исследуемая функция 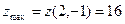 .
. .
. , аналогично
, аналогично  . Критическими снова могут быть только стационарные точки. Для нахождения координат таких точек решаем систему
. Критическими снова могут быть только стационарные точки. Для нахождения координат таких точек решаем систему  . Деля обе части первого уравнения на 2, второго – на 4 и перенося числа в правую часть, получим следующую систему для определения координат стационарных точек:
. Деля обе части первого уравнения на 2, второго – на 4 и перенося числа в правую часть, получим следующую систему для определения координат стационарных точек:  . Оказывается, что эта система несовместна, т.е. не имеет ни одного решения. Это можно доказать с помощью теоремы Кронекера- Капели (эта теорема была в разделе «Основы линейной алгебры»), убедившись, что ранги основной и расширенной матриц системы не совпадают. Если эти методы уже забылись, то можно действовать и «школьными» приемами. Для этого выразим из первого уравнения
. Оказывается, что эта система несовместна, т.е. не имеет ни одного решения. Это можно доказать с помощью теоремы Кронекера- Капели (эта теорема была в разделе «Основы линейной алгебры»), убедившись, что ранги основной и расширенной матриц системы не совпадают. Если эти методы уже забылись, то можно действовать и «школьными» приемами. Для этого выразим из первого уравнения  и подставим во второе:
и подставим во второе:  ,
,  ,
, 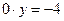 . Последнее уравнение, очевидно, решений не имеет, так как не существует такого числа, которое, будучи умноженным на 0, даст
. Последнее уравнение, очевидно, решений не имеет, так как не существует такого числа, которое, будучи умноженным на 0, даст 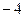 . Поэтому и вся система решений не имеет. Что же это означает? Решения этой системы давали нам координаты критических точек. Отсутствие решений системы говорит об отсутствии критических точек у исследуемой функции. Но поскольку все экстремумы функции находятся только среди ее критических точек, то у данной функции экстремумов нет.
. Поэтому и вся система решений не имеет. Что же это означает? Решения этой системы давали нам координаты критических точек. Отсутствие решений системы говорит об отсутствии критических точек у исследуемой функции. Но поскольку все экстремумы функции находятся только среди ее критических точек, то у данной функции экстремумов нет.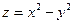 .
. ,
,  . Ищем координаты критических точек:
. Ищем координаты критических точек:  . Ясно, что система имеет единственное решение
. Ясно, что система имеет единственное решение  ,
,  ,
,  . Тогда
. Тогда  ,
,  ,
,  . Итак,
. Итак, 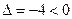 , потому по приведенной выше теореме экстремумов в точке
, потому по приведенной выше теореме экстремумов в точке  .
. ,
,  . Оба получившихся выражения для производных определены при любых значениях
. Оба получившихся выражения для производных определены при любых значениях  . Сокращая уравнения на 3, получим
. Сокращая уравнения на 3, получим  . Выражаем из первого уравнения
. Выражаем из первого уравнения 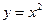 и подставляем во второе:
и подставляем во второе:  ,
,  ,
,  . Произведение может обратиться в 0 только при тех значениях
. Произведение может обратиться в 0 только при тех значениях  , т.е.
, т.е.  . Таким образом, уравнение имеет два корня:
. Таким образом, уравнение имеет два корня: 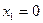 и
и  . Учитывая полученную ранее связь
. Учитывая полученную ранее связь  ,
,  . Потому система имеет 2 решения:
. Потому система имеет 2 решения:  ,
,  и
и  , а исследуемая функция имеет, соответственно, две критические точки:
, а исследуемая функция имеет, соответственно, две критические точки:  и
и  . В соответствии с дальнейшими пунктами схемы, находим выражения для вторых производных:
. В соответствии с дальнейшими пунктами схемы, находим выражения для вторых производных:  ,
, 
 .
. ,
, 
 . Тогда число
. Тогда число  . Поскольку число
. Поскольку число  , то (в соответствии с описанной схемой) исследуемая критическая точка
, то (в соответствии с описанной схемой) исследуемая критическая точка  . Вычисляем в этой точке значения вторых производных:
. Вычисляем в этой точке значения вторых производных: 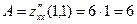 ,
, 
 . Тогда число
. Тогда число  . Поскольку число
. Поскольку число 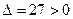 , то (в соответствии с описанной схемой) исследуемая критическая точка
, то (в соответствии с описанной схемой) исследуемая критическая точка  , то
, то  .
. .
. .
. ={производная произведения:
={производная произведения:  }=
}= 
 , аналогично
, аналогично  {первый множитель не содержит
{первый множитель не содержит  . Оба получившихся выражения для производных определены при любых значениях
. Оба получившихся выражения для производных определены при любых значениях  . Поскольку
. Поскольку  не обращается в 0 ни при каких значениях показателя степени
не обращается в 0 ни при каких значениях показателя степени  , получим систему, равносильную исходной:
, получим систему, равносильную исходной:  . Подставляя
. Подставляя  . Итак, единственным решением системы является пара чисел:
. Итак, единственным решением системы является пара чисел:  . Далее, находим вторые производные:
. Далее, находим вторые производные: 

 ,
,  ,
, 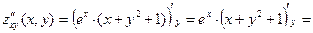
 . Вычисляем значения вторых производных в исследуемой критической точке
. Вычисляем значения вторых производных в исследуемой критической точке  ,
, 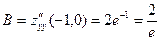
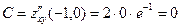 . Тогда число
. Тогда число  . Поэтому исследуемая критическая точка
. Поэтому исследуемая критическая точка  , то это точка минимума. Минимальное значение функции
, то это точка минимума. Минимальное значение функции  . Итак, функция
. Итак, функция  .
. Пример 9. Необходимо построить открытый бассейн в форме прямого параллелепипеда объемом
Пример 9. Необходимо построить открытый бассейн в форме прямого параллелепипеда объемом 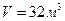 , на облицовку дна и стен которого пойдет наименьшее количество материала.
, на облицовку дна и стен которого пойдет наименьшее количество материала. (см. рисунок). Понятно, что чем меньше необходимая площадь облицовки, тем меньше будет использовано облицовочного материала. Таким образом, встает следующая задача. Подобрать такие числа
(см. рисунок). Понятно, что чем меньше необходимая площадь облицовки, тем меньше будет использовано облицовочного материала. Таким образом, встает следующая задача. Подобрать такие числа  был равен
был равен  , а суммарная площадь основания и боковой поверхности (это как раз дно и стены бассейна) была бы наименьшей. Выразим эту площадь через размеры параллелепипеда. Указанная площадь (обозначим ее
, а суммарная площадь основания и боковой поверхности (это как раз дно и стены бассейна) была бы наименьшей. Выразим эту площадь через размеры параллелепипеда. Указанная площадь (обозначим ее  ) складывается из площади прямоугольника-основания (равной
) складывается из площади прямоугольника-основания (равной  ), площадей передней и задней стенок (равных
), площадей передней и задней стенок (равных  каждая) и площадей левой и правой стенок (по
каждая) и площадей левой и правой стенок (по  каждая). Таким образом, площадь облицовки
каждая). Таким образом, площадь облицовки  или
или  . Требуется найти точку минимума этой функции. Поскольку мы изучили методы отыскания экстремумов функции двух (а не трех) переменных, то от одной переменной надо избавиться. Это можно сделать, если понять, что размеры бассейна
. Требуется найти точку минимума этой функции. Поскольку мы изучили методы отыскания экстремумов функции двух (а не трех) переменных, то от одной переменной надо избавиться. Это можно сделать, если понять, что размеры бассейна  , откуда
, откуда 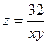 . Поэтому если выбраны длина
. Поэтому если выбраны длина  . Подставляя это выражение в полученную выше формулу
. Подставляя это выражение в полученную выше формулу  . Раскрывая скобки, получим более удобное для исследования выражение:
. Раскрывая скобки, получим более удобное для исследования выражение:  или
или  . По смыслу задачи (
. По смыслу задачи ( ,
,  . Поэтому областью определения этой функции является I четверть без точек, лежащих на осях координат. Найдем экстремумы этой функции двух переменных по привычной схеме. Находим первые производные:
. Поэтому областью определения этой функции является I четверть без точек, лежащих на осях координат. Найдем экстремумы этой функции двух переменных по привычной схеме. Находим первые производные: 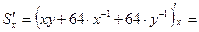
 . Таким образом,
. Таким образом,  или
или  . Аналогично можно получить выражение для другой частной производной:
. Аналогично можно получить выражение для другой частной производной:  или
или  . Находим критические точки. Производная
. Находим критические точки. Производная  . Аналогично, производная
. Аналогично, производная  . Однако все эти точки не входят в область определения исследуемой функции, а потому не являются критическими точками функции и не интересуют нас как потенциальные точки экстремума. Найдем теперь те критические точки функции, которые являются ее стационарными точками. Для нахождения координат этих точек решаем систему
. Однако все эти точки не входят в область определения исследуемой функции, а потому не являются критическими точками функции и не интересуют нас как потенциальные точки экстремума. Найдем теперь те критические точки функции, которые являются ее стационарными точками. Для нахождения координат этих точек решаем систему  , т.е.
, т.е.  . Из первого уравнения выразим
. Из первого уравнения выразим 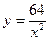 и подставим во второе уравнение:
и подставим во второе уравнение:  ,
, 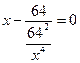 ,
, 


