
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Точка условного экстремума является точкой экстремума функцииСодержание книги
Поиск на нашем сайте
6. При исследовании функции на экстремум рекомендуется пользоваться следующей схемой: 1. Найти частные производные z'x и z'y. 2. Решить систему уравнений 3. Найти частные производные второго порядка, вычислить их значения в каждой критической точке и с помощью достаточного условия сделать вывод о наличии экстремумов. 4. Найти экстремумы (экстремальные значения) функции.
Пример. Найти экстремумы функции Решение. 1. Находим частные производные:
2. Находим критические точки функции из системы Получаем х = -2, у = 0, т.е. (-2; 0) - единственная критическая точка.
3. Находим частные производные второго порядка:
Имеем В точке (-2; 0) имеем (-2; 0) — точка минимума. 4. Находим минимум функции Пример. Найти экстремумы функции Решение. Первый способ. При условии х2 + у2 = 1 имеем
Критические точки задаются равенствами Легко проверить, что Второй способ. Функция Лагранжаимеет вид:
Приравнивая ее частные производные к нулю, получаем систему:
Из уравнений (1) и (2) находим у = 2 х, подставляя в (3), получаем два решения
Задания для самостоятельного решения
1. Найти локальные экстремумы функции и установить их характер: 1) u = 4x 2) u = -x 3) u = -4x 4) u = x 5) u = 0,5x
2. Для функций пунктов 1-3 и 5 предыдущего раздела найти локальные экстремумы при ограничении 2x + y = 8 3. Найти локальный и условный экстремумы производственной функции Q = a – (K – 2a)
Задания для самостоятельного решения
1. Найти вторую смешанную производную функции u = x ln y - e 2. Найти вторую смешанную производную функции u = 3. F(x,y) = 4. Найти дифференциал функции u = d x = 0,4 = d y. 5. Найти вторую смешанную производную функции u = x 6. Для функции спроса Q = 120 – lg P + 2P Р 7. Задача функция спроса Q = 3Y P 8. Для функции спроса Q = 20 – ln(P/P Р 9. Для функции спроса Q = 4Y 10. Для функции спроса Q = -50 - P 11. Для функции полезности u = 3 12. Для производственной функции Кобба-Дугласа Q = 3
13. Для производственной функции, заданной в форме Кобба-Дугласа: 14. Q = 4 15. в точке М (K;L) = (16;256). 16. Производственная функция задана в виде Q = 5 17. Для функции полезности u = 4 18. Для функции u = x 19. Для функции u = 4x 20. Для функции u = x 21. Для функции u = -3x 22. Для функции u = 2x 23. Для функции u, приведенной в задании 4, найти локальный экстремум при ограничении x + 3y = 21. 24. Для функции u, приведенной в задании 4, найти локальный экстремум при ограничении x + 5y + 12 = 0. 25. Для функции u, приведенной в задании 4, найти локальный экстремум при ограничении 3x + y = 6. 26. Для функции u, приведенной в задании 4, найти локальный экстремум при ограничении 3x + y = 7. 27. Для функции u, приведенной в задании 4, найти локальный экстремум при ограничении 2x + y = 10. 28. x 29. x 30. Найти 31. y 32. 4x
Интегральное исчисление. Неопределенный интеграл Функция F(x) называется первообразной функции f (х) на некотором промежутке D, если для всех x из D выполняется: Например, F (х)=sinх является первообразной для функций f (х) = cos x на всей числовой прямой, т. к. Если F(х) — первообразная для функции f (х), то любая другая первообразная для f(х) может быть представлена в виде F(х)+ С, где С —произвольная постоянная. Неопределенным интегралом от функции f (х) называется множество всех первообразных этой функции и обозначается
Согласно определению,
Свойства дифференциала: 1. dc = 0, где с = const, 2. 3. d(u+ v)=du + dv, 4. d (u×v)= u×dv + v×du, 5.
|
||
|
Последнее изменение этой страницы: 2016-12-15; просмотров: 457; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.006 с.) |

 . Функция L называется функцией Лагранжа,а l— множителем Лагранжа.
. Функция L называется функцией Лагранжа,а l— множителем Лагранжа. ,
,  и найти критические точки функции.
и найти критические точки функции. .
. ;
;  .
.
 ;
; ;
;  .
. .
.
 . Таким образом,
. Таким образом, .
. при условии, что
при условии, что 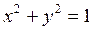 .
. и получаем две функции одной переменной
и получаем две функции одной переменной 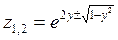 ;
; .
. , т.е.
, т.е.  . Таким образом, имеем две критические точки
. Таким образом, имеем две критические точки  и
и  .
. .
.
 ,
,  и
и  ,
,  . Таким образом, получаем те же две критические точки
. Таким образом, получаем те же две критические точки  + 6xy + 3y
+ 6xy + 3y 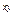
 + x
+ x  -
-  + 3yx
+ 3yx  + 5x, найти
+ 5x, найти  -?
-? .
. + 0,1Y. (P – цена,
+ 0,1Y. (P – цена, - альтернативная цена, Y – доход потребителя) найти эластичность спроса от альтернативной цены при Р = 10
- альтернативная цена, Y – доход потребителя) найти эластичность спроса от альтернативной цены при Р = 10  /
/ 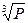 (Р – цена, Р
(Р – цена, Р  , Р
, Р 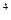 , Y = 100.
, Y = 100. (Р – цена, Р - альтернативная цена, Y – доход потребителя) найти эластичность спроса от цены и перекрестный коэффициент эластичности в точке М (Р;Р
(Р – цена, Р - альтернативная цена, Y – доход потребителя) найти эластичность спроса от цены и перекрестный коэффициент эластичности в точке М (Р;Р  + 0,2Y (Р – цена, Р
+ 0,2Y (Р – цена, Р 
 записать уравнение кривой безразличия, проходящей через точку М (x;y) = M (8;32). Найти в этой точке предельные полезности для x и y.
записать уравнение кривой безразличия, проходящей через точку М (x;y) = M (8;32). Найти в этой точке предельные полезности для x и y.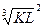 записать уравнение кривой безразличия, проходящей через точку M (K;L) = M (8;27). Найти в этой точке предельные продукты капитала и труда.
записать уравнение кривой безразличия, проходящей через точку M (K;L) = M (8;27). Найти в этой точке предельные продукты капитала и труда. , найти коэффициент заменяемости ресурса К
, найти коэффициент заменяемости ресурса К . Найти предельные продукты капитала К и труда L для K = 2; L = 64 и приращение Q выпуска продукции при заданных K и L, если K = 2, L = 1.
. Найти предельные продукты капитала К и труда L для K = 2; L = 64 и приращение Q выпуска продукции при заданных K и L, если K = 2, L = 1.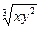 найти предельную полезность по x при u
найти предельную полезность по x при u  = 108, x
= 108, x  = 27 и изменение полезности при заданных значениях переменных, если x = 37 и y = 0.
= 27 и изменение полезности при заданных значениях переменных, если x = 37 и y = 0. + ln x -
+ ln x -  = 0,
= 0,  -?
-? + ln y – 2xy
+ ln y – 2xy  = 0,
= 0, 
 для всех х.
для всех х.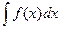 ; здесь
; здесь  — знак интеграла, f (х) — подынтегральная функция, х — переменная интегрирования.
— знак интеграла, f (х) — подынтегральная функция, х — переменная интегрирования. , где
, где 

 ,
,



