
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Фундаментальная система решений.Содержание книги
Поиск на нашем сайте
Система m линейных уравнений с n переменными называется системой линейных однородных уравнений, если все их свободные члены равны нулю.
Система линейных однородных уравнений всегда совместна, т.к. она всегда имеет, по крайней мере, нулевое (тривиальное) решение (0;0;…;0).
Если в системе (2) m=n, а её определитель отличен от нуля, то такая система имеет только нулевое решение, как это следует из теоремы и формул Крамера.
Ненулевые решения, возможны лишь для таких систем линейных однородных уравнений, в которых число уравнений меньше числа переменных или, когда m=n, но определитель системы равен нулю. Иначе: система линейных однородных уравнений имеет ненулевые решения тогда и только тогда, когда ранг её матрицы коэффициентов при переменных меньше числа переменных, т.е. Обозначим решение системы
в виде строки Свойства решений системы линейных однородных уравнений. 1. Если строка 2. Если строки Из свойств следует, что всякая линейная комбинация решений системы линейных однородных уравнений также является решением этой системы. Определение. Система линейно независимых решений
Теорема: Если ранг матрицы коэффициентов при переменных системы линейных однородных уравнений (2) меньше числа переменных n, то всякая фундаментальная система решений системы (2) состоит из n-r решений.
Поэтому общее решение системы (2) линейных однородных уравнений имеет вид:
где
Пример решения задач. Пример. Найти фундаментальную систему решений системы линейных однородных алгебраических уравнений.
Такая система совместна всегда, так как имеет тривиальное решение (0; 0; 0; 0; 0).
Решение.
Условия для нахождения фундаментальных решений:
1)
2)
3)
Данные строки - РАСЧЕТНО-ГРАФИЧЕСКИЕ РАБОТЫ Расчетная работа № 1. Обработка экспериментальных данных Методом наименьших квадратов Основные положения При обработке данных экспериментов возникает необходимость определения закономерности их изменения: - представление в виде какой-либо функциональной зависимости с целью исследования и прогнозирования характера и протекания процесса; Из методов построения эмпирической прямой наиболее обоснован и распространён метод наименьших квадратов, заключающийся в следующем: - из множества функциональных зависимостей определённого вида выбирается та, для которой сумма квадратов отклонений экспериментальных значений от теоретических (вычислительных) является наименьшей.
|
|||||
|
Последнее изменение этой страницы: 2016-12-15; просмотров: 509; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.227.134.162 (0.008 с.) |

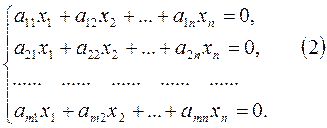
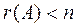 .
.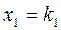 ,
, 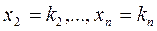
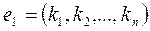 .
.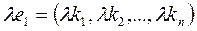 -также решение этой системы.
-также решение этой системы.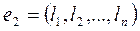 -решения системы (2), то при
-решения системы (2), то при 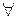
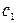 и
и 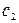 их линейная комбинация
их линейная комбинация 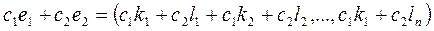 -так же решение этой системы.
-так же решение этой системы. называется фундаментальной, если каждое решение системы является линейной комбинацией решений
называется фундаментальной, если каждое решение системы является линейной комбинацией решений 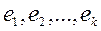 .
.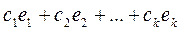 ,
,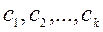 -произвольные числа,
-произвольные числа,  .
.
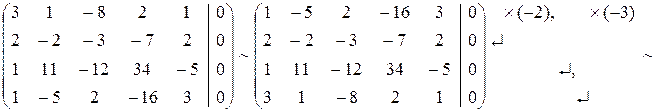
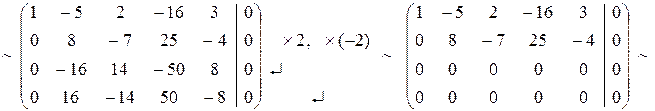
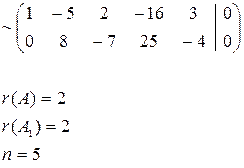
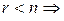 система имеет множество решений.
система имеет множество решений.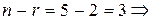 система имеет три свободные переменные
система имеет три свободные переменные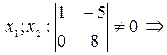
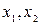 - базисные переменные,
- базисные переменные, 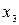 ,
, 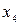 ,
, 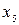 - свободные переменные
- свободные переменные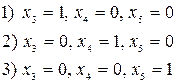
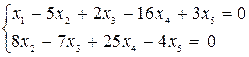

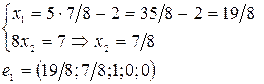
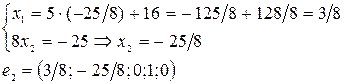
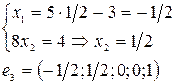
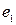 ,
, 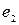 ,
, 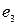 (векторы) – образуют фундаментальную систему решений данной системы линейных однородных алгебраических уравнений.
(векторы) – образуют фундаментальную систему решений данной системы линейных однородных алгебраических уравнений.


