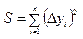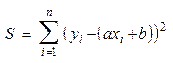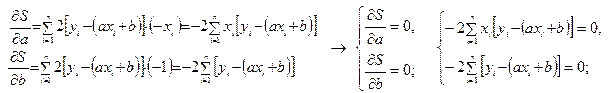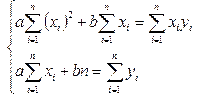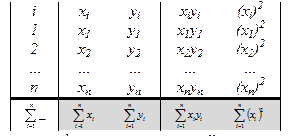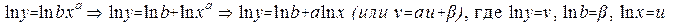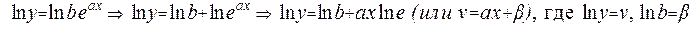Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Отправной точкой обработки данных является выбор вида функциональной зависимости.Содержание книги
Поиск на нашем сайте
Пусть данные опыта представляют собой некоторое кол-во n -точек с координатами (xi;yi), (i= 1; 2; …; n)
Если в таблице участвуют две величины, то получают зависимость в видефункции одной переменной y(x) или x(y).
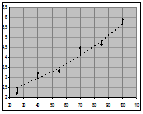 Удобно изображать эти процессы графически Удобно изображать эти процессы графически
Можно этот набор точек попытаться описать прямой типа (y=ax+b), можно считать, что это часть параболы (y=ax2+bx+c), степенно-показательной (y=beax) или обобщённо-степенной (y=bxa) функции.
Согласно методу наименьших квадратов, параметры функции f(x) следует выбирать так, чтобы сумма квадратов отклонений была наименьшей, а значит минимизировались отклонения статистических данных от теоретических. Этот метод постоянно используется в статистике, эконометрике, в финансовой математике и т.д. Часто такой метод называют получением уравнений регрессии методом наименьших квадратов по сущности вычислительной процедуры. Это классическая задача дифференциального исчисления. Рассмотрим применение данного метода для получения эмпирических формул на примере линейной функции y=ax+b Пусть принято решение искать эмпирическую формулу в виде линейной функции.
При этом a и b являются переменными. Определим функцию Для нахождения экстремума функции 2-х переменных необходимо найти частные производные данной функции по каждой переменной, приравнять их к нулю, и решив полученную систему двух уравнений, определить критические значения a и b.
После преобразований получим следующую систему
Найденные значения a и b соответствуют min функции S. Расчет значений известных величин, входящих в уравнения системы, удобно вести с помощью таблиц.
Подставляя найденные значения коэффициентов при a и b в систему уравнений, получаем значения неизвестных a и b. Таким образом эмпирическая формула будет найдена. Графиком её является прямая, проходящая наиболее близко ко всем экспериментальным точкам.
Рассмотрим функцию вида у=bxa (обобщенно-степенная функция) Прологарифмируем её.
Теперь линейное уравнение рассмотрим не для табличных значений, а для их логарифмов:
Расчет значений, входящих в уравнения системы, удобно вести с помощью таблиц. Рассмотрим функцию вида у=beax (степенно-показательная функция) Прологарифмируем её:
Теперь линейное уравнение рассмотрим не для табличных значений, а для их логарифмов:
Расчет значений, входящих в уравнения системы, удобно вести с помощью таблиц.
|
|||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-15; просмотров: 363; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.222.253.118 (0.006 с.) |

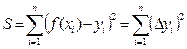
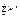 Очевидно, что в искомом уравнении линейной функции y=ax+b неизвестными являются коэффициенты a и b, при этом их значение должно обеспечить минимальное суммарное отклонение экспериментальных данных от теоретических, т.е. обеспечить прохождение прямой наиболее близко ко всем экспериментальным точкам. Данная цель достигается при минимальной величине суммы квадратов отклонений.
Очевидно, что в искомом уравнении линейной функции y=ax+b неизвестными являются коэффициенты a и b, при этом их значение должно обеспечить минимальное суммарное отклонение экспериментальных данных от теоретических, т.е. обеспечить прохождение прямой наиболее близко ко всем экспериментальным точкам. Данная цель достигается при минимальной величине суммы квадратов отклонений.